Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 87419 by john santu last updated on 04/Apr/20

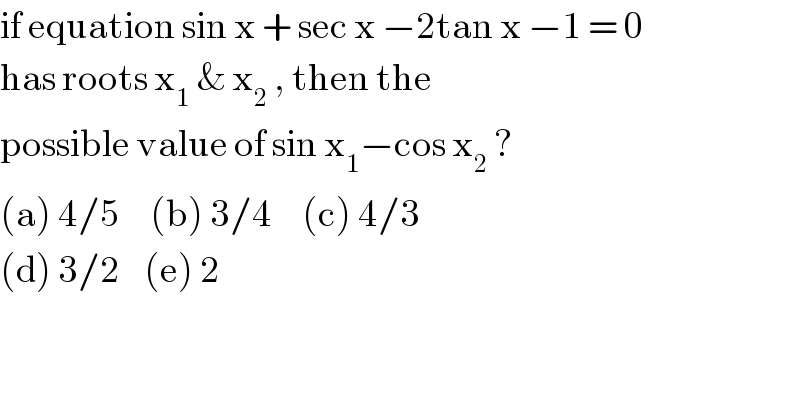
if equation sin x + sec x −2tan x −1 = 0 has roots x_1 & x_2 , then the possible value of sin x_1 −cos x_2 ? (a) 4/5 (b) 3/4 (c) 4/3 (d) 3/2 (e) 2

$$\mathrm{if}\:\mathrm{equation}\:\mathrm{sin}\:\mathrm{x}\:+\:\mathrm{sec}\:\mathrm{x}\:−\mathrm{2tan}\:\mathrm{x}\:−\mathrm{1}\:=\:\mathrm{0} \\ $$ $$\mathrm{has}\:\mathrm{roots}\:\mathrm{x}_{\mathrm{1}} \:\&\:\mathrm{x}_{\mathrm{2}} \:,\:\mathrm{then}\:\mathrm{the}\: \\ $$ $$\mathrm{possible}\:\mathrm{value}\:\mathrm{of}\:\mathrm{sin}\:\mathrm{x}_{\mathrm{1}} −\mathrm{cos}\:\mathrm{x}_{\mathrm{2}} \:? \\ $$ $$\left(\mathrm{a}\right)\:\mathrm{4}/\mathrm{5}\:\:\:\:\:\left(\mathrm{b}\right)\:\mathrm{3}/\mathrm{4}\:\:\:\:\:\left(\mathrm{c}\right)\:\mathrm{4}/\mathrm{3}\: \\ $$ $$\left(\mathrm{d}\right)\:\mathrm{3}/\mathrm{2}\:\:\:\:\left(\mathrm{e}\right)\:\mathrm{2} \\ $$

Commented byjohn santu last updated on 04/Apr/20

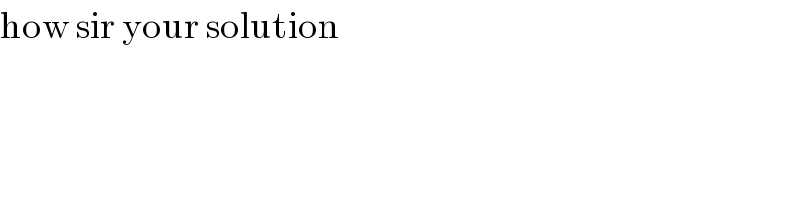
how sir your solution

$$\mathrm{how}\:\mathrm{sir}\:\mathrm{your}\:\mathrm{solution} \\ $$

Commented byMJS last updated on 04/Apr/20

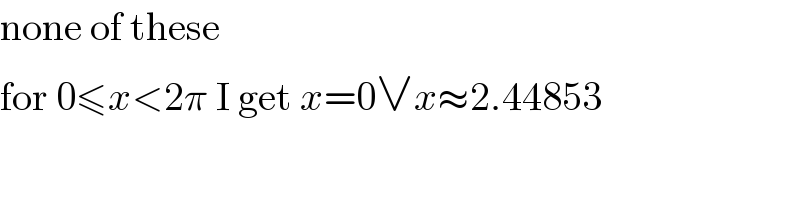
none of these for 0≤x<2π I get x=0∨x≈2.44853

$$\mathrm{none}\:\mathrm{of}\:\mathrm{these} \\ $$ $$\mathrm{for}\:\mathrm{0}\leqslant{x}<\mathrm{2}\pi\:\mathrm{I}\:\mathrm{get}\:{x}=\mathrm{0}\vee{x}\approx\mathrm{2}.\mathrm{44853} \\ $$

Commented byjohn santu last updated on 04/Apr/20

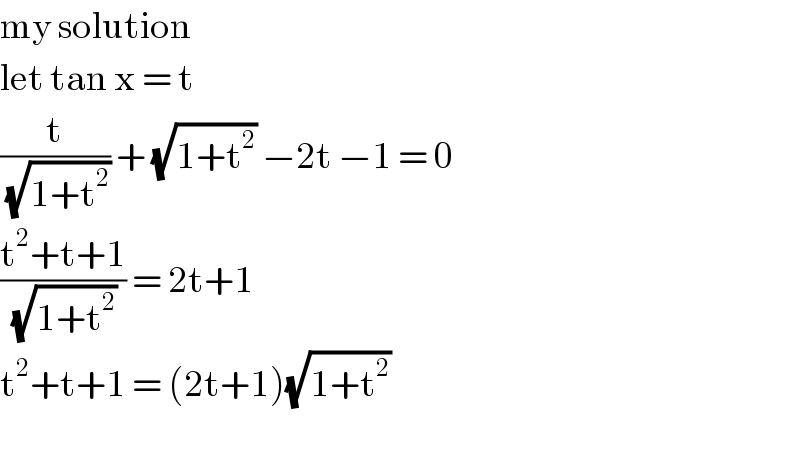
my solution let tan x = t (t/(√(1+t^2 ))) + (√(1+t^2 )) −2t −1 = 0 ((t^2 +t+1)/(√(1+t^2 ))) = 2t+1 t^2 +t+1 = (2t+1)(√(1+t^2 ))

$$\mathrm{my}\:\mathrm{solution}\: \\ $$ $$\mathrm{let}\:\mathrm{tan}\:\mathrm{x}\:=\:\mathrm{t}\: \\ $$ $$\frac{\mathrm{t}}{\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\:+\:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:−\mathrm{2t}\:−\mathrm{1}\:=\:\mathrm{0} \\ $$ $$\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{t}+\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\:=\:\mathrm{2t}+\mathrm{1}\: \\ $$ $$\mathrm{t}^{\mathrm{2}} +\mathrm{t}+\mathrm{1}\:=\:\left(\mathrm{2t}+\mathrm{1}\right)\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$ $$ \\ $$

Commented byjohn santu last updated on 04/Apr/20

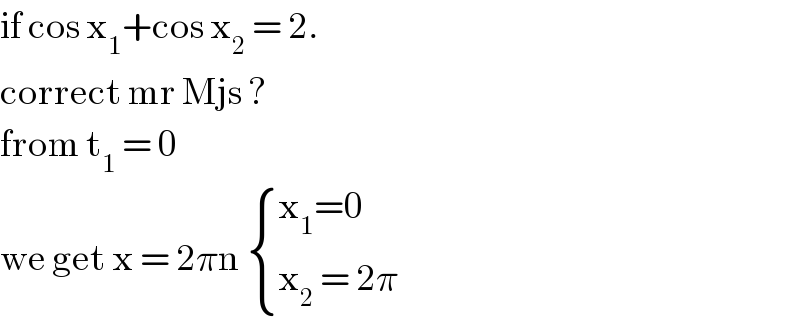
if cos x_1 +cos x_2 = 2. correct mr Mjs ? from t_1 = 0 we get x = 2πn { ((x_1 =0)),((x_2 = 2π)) :}

$$\mathrm{if}\:\mathrm{cos}\:\mathrm{x}_{\mathrm{1}} +\mathrm{cos}\:\mathrm{x}_{\mathrm{2}} \:=\:\mathrm{2}. \\ $$ $$\mathrm{correct}\:\mathrm{mr}\:\mathrm{Mjs}\:? \\ $$ $$\mathrm{from}\:\mathrm{t}_{\mathrm{1}} \:=\:\mathrm{0} \\ $$ $$\mathrm{we}\:\mathrm{get}\:\mathrm{x}\:=\:\mathrm{2}\pi\mathrm{n}\:\begin{cases}{\mathrm{x}_{\mathrm{1}} =\mathrm{0}}\\{\mathrm{x}_{\mathrm{2}} \:=\:\mathrm{2}\pi}\end{cases} \\ $$

Commented byMJS last updated on 04/Apr/20

this is somehow true but the given equation has infinite solutions and it′s asked for 2 solutions x_1 and x_2 . I think x_1 ≠x_2 ∧x_1 ≠x_2 +2nπ but anyway sin x_1 −cos x_2 ≠ any of the given options the question is very strange...

$$\mathrm{this}\:\mathrm{is}\:\mathrm{somehow}\:\mathrm{true}\:\mathrm{but}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$ $$\mathrm{has}\:\mathrm{infinite}\:\mathrm{solutions}\:\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{asked}\:\mathrm{for}\:\mathrm{2} \\ $$ $$\mathrm{solutions}\:{x}_{\mathrm{1}} \:\mathrm{and}\:{x}_{\mathrm{2}} .\:\mathrm{I}\:\mathrm{think}\:{x}_{\mathrm{1}} \neq{x}_{\mathrm{2}} \wedge{x}_{\mathrm{1}} \neq{x}_{\mathrm{2}} +\mathrm{2}{n}\pi \\ $$ $$\mathrm{but}\:\mathrm{anyway}\:\mathrm{sin}\:{x}_{\mathrm{1}} \:−\mathrm{cos}\:{x}_{\mathrm{2}} \:\neq\:\mathrm{any}\:\mathrm{of}\:\mathrm{the} \\ $$ $$\mathrm{given}\:\mathrm{options} \\ $$ $$\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{very}\:\mathrm{strange}... \\ $$

Commented byjohn santu last updated on 04/Apr/20

yes sir i agree

$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{agree} \\ $$

Answered by MJS last updated on 04/Apr/20

t=tan (x/2) ⇔ x=2arctan t ((−2t(t^3 −3t^2 +t−1))/(t^4 −1))=0 t_1 =0 t^3 −3t^2 +t−1=0 t=z+1 z^3 −2z−2=0 D=(((−2)^3 )/(27))+(((−2)^2 )/4)=((19)/(27))>0 ⇒ Cardano z=((1+((√(57))/9)))^(1/3) +((1−((√(57))/9)))^(1/3) ⇒ t_2 =1+((1+((√(57))/9)))^(1/3) +((1−((√(57))/9)))^(1/3) ≈2.76929 ⇒ x_1 =0 x_2 =2arctan (1+((1+((√(57))/9)))^(1/3) +((1−((√(57))/9)))^(1/3) ) ≈2.44853

$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\Leftrightarrow\:{x}=\mathrm{2arctan}\:{t} \\ $$ $$\frac{−\mathrm{2}{t}\left({t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +{t}−\mathrm{1}\right)}{{t}^{\mathrm{4}} −\mathrm{1}}=\mathrm{0} \\ $$ $${t}_{\mathrm{1}} =\mathrm{0} \\ $$ $${t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +{t}−\mathrm{1}=\mathrm{0} \\ $$ $${t}={z}+\mathrm{1} \\ $$ $${z}^{\mathrm{3}} −\mathrm{2}{z}−\mathrm{2}=\mathrm{0} \\ $$ $${D}=\frac{\left(−\mathrm{2}\right)^{\mathrm{3}} }{\mathrm{27}}+\frac{\left(−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{19}}{\mathrm{27}}>\mathrm{0}\:\Rightarrow\:\mathrm{Cardano} \\ $$ $${z}=\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{\sqrt{\mathrm{57}}}{\mathrm{9}}}+\sqrt[{\mathrm{3}}]{\mathrm{1}−\frac{\sqrt{\mathrm{57}}}{\mathrm{9}}} \\ $$ $$\Rightarrow\:{t}_{\mathrm{2}} =\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{\sqrt{\mathrm{57}}}{\mathrm{9}}}+\sqrt[{\mathrm{3}}]{\mathrm{1}−\frac{\sqrt{\mathrm{57}}}{\mathrm{9}}}\approx\mathrm{2}.\mathrm{76929} \\ $$ $$\Rightarrow \\ $$ $${x}_{\mathrm{1}} =\mathrm{0} \\ $$ $${x}_{\mathrm{2}} =\mathrm{2arctan}\:\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{\sqrt{\mathrm{57}}}{\mathrm{9}}}+\sqrt[{\mathrm{3}}]{\mathrm{1}−\frac{\sqrt{\mathrm{57}}}{\mathrm{9}}}\right)\:\approx\mathrm{2}.\mathrm{44853} \\ $$

Commented byjohn santu last updated on 04/Apr/20

i′m stuck in Cardano sir

$$\mathrm{i}'\mathrm{m}\:\mathrm{stuck}\:\mathrm{in}\:\mathrm{Cardano}\:\mathrm{sir} \\ $$

Commented byMJS last updated on 04/Apr/20

x^3 +ax^2 +bx+c=0 let x=t−(a/3) t^3 −((a^2 −3b)/3)t+((2a^3 −9ab+27c)/(27))=0 −((a^2 −3b)/3)=p∧((2a^3 −9ab+27c)/(27))=q t^3 +pt+q=0 D=(p^3 /(27))+(q^2 /4) { ((>0 ⇒ Cardano)),((<0 ⇒ trigonimetric solution)) :} Cardano u=((−(q/2)+(√((p^3 /(27))+(q^2 /4)))))^(1/3) v=((−(q/2)−(√((p^3 /(27))+(q^2 /4)))))^(1/3) [we need the real roots i.e. ((−1))^(1/3) =−1] t_1 =u+v t_2 =(−(1/2)−((√3)/2)i)u+(−(1/2)+((√3)/2)i)v t_3 =(−(1/2)+((√3)/2)i)u+(−(1/2)−((√3)/2)i)v trigononetric solution t_(j+1) =((2(√(−3p)))/3)sin (((2jπ)/3)−(1/3)arcsin ((3(√3)q)/(2p(√(−p))))) with j=0, 1, 2

$${x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$ $$\mathrm{let}\:{x}={t}−\frac{{a}}{\mathrm{3}} \\ $$ $${t}^{\mathrm{3}} −\frac{{a}^{\mathrm{2}} −\mathrm{3}{b}}{\mathrm{3}}{t}+\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{9}{ab}+\mathrm{27}{c}}{\mathrm{27}}=\mathrm{0} \\ $$ $$−\frac{{a}^{\mathrm{2}} −\mathrm{3}{b}}{\mathrm{3}}={p}\wedge\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{9}{ab}+\mathrm{27}{c}}{\mathrm{27}}={q} \\ $$ $${t}^{\mathrm{3}} +{pt}+{q}=\mathrm{0} \\ $$ $${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}\:\begin{cases}{>\mathrm{0}\:\Rightarrow\:\mathrm{Cardano}}\\{<\mathrm{0}\:\Rightarrow\:\mathrm{trigonimetric}\:\mathrm{solution}}\end{cases} \\ $$ $$ \\ $$ $$\mathrm{Cardano} \\ $$ $${u}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}}{v}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}−\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}} \\ $$ $$\:\:\:\:\:\left[\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{i}.\mathrm{e}.\:\sqrt[{\mathrm{3}}]{−\mathrm{1}}=−\mathrm{1}\right] \\ $$ $${t}_{\mathrm{1}} ={u}+{v} \\ $$ $${t}_{\mathrm{2}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){u}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){v} \\ $$ $${t}_{\mathrm{3}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){u}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){v} \\ $$ $$ \\ $$ $$\mathrm{trigononetric}\:\mathrm{solution} \\ $$ $${t}_{{j}+\mathrm{1}} =\frac{\mathrm{2}\sqrt{−\mathrm{3}{p}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{2}{j}\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}{q}}{\mathrm{2}{p}\sqrt{−{p}}}\right) \\ $$ $$\mathrm{with}\:{j}=\mathrm{0},\:\mathrm{1},\:\mathrm{2} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com