
Question and Answers Forum
Question Number 87461 by hamdhan last updated on 04/Apr/20
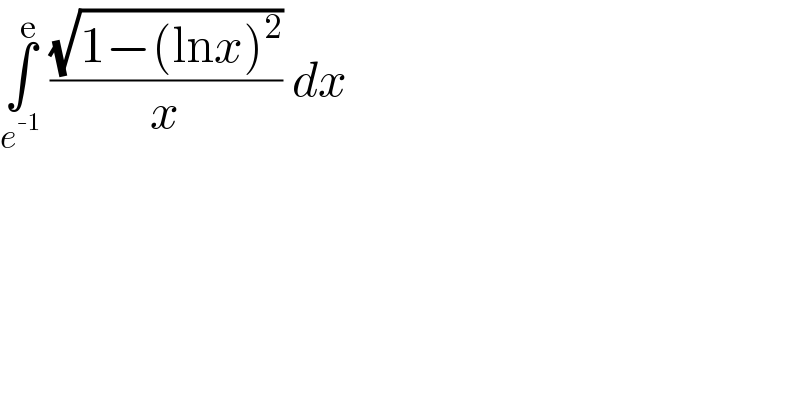
Commented by ajfour last updated on 04/Apr/20
![let ln x=t ⇒ (dx)/x=dt I=2∫_0 ^( 1) (√(1−t^2 )) dt = [t(√(1−t^2 ))+sin^(−1) t ]_0 ^1 = π/2 .](Q87463.png)
Answered by Ar Brandon last updated on 04/Apr/20
![Let x=e^y ⇒dx=e^y dy I=∫_(−1) ^1 ((√(1−y^2 ))/e^y )∙e^y dy= ∫_(−1) ^1 (√(1−y^2 ))dy I=(√(1−y^2 ))∫_(−1) ^1 dy−∫_(−1) ^1 [(d/dy)((√(1−y^2 )))∫dy]dy =[y(√(1−y^2 ))]_(−1) ^1 +∫_(−1) ^1 [(y^2 /(√(1−y^2 )))]dy let y=sin θ ⇒dy=cos θdθ I=∫_(−(π/2)) ^(π/2) sin^2 θ dθ=(1/2)∫_(−(π/2)) ^(π/2) (1−cos(2θ))dθ I=(1/2)[θ−(1/2)sin(2θ)]_(−(π/2)) ^(π/2) I=(1/2)[(π/2)+(π/2)]=(π/2)](Q87465.png)
| ||
Question and Answers Forum | ||
Question Number 87461 by hamdhan last updated on 04/Apr/20 | ||
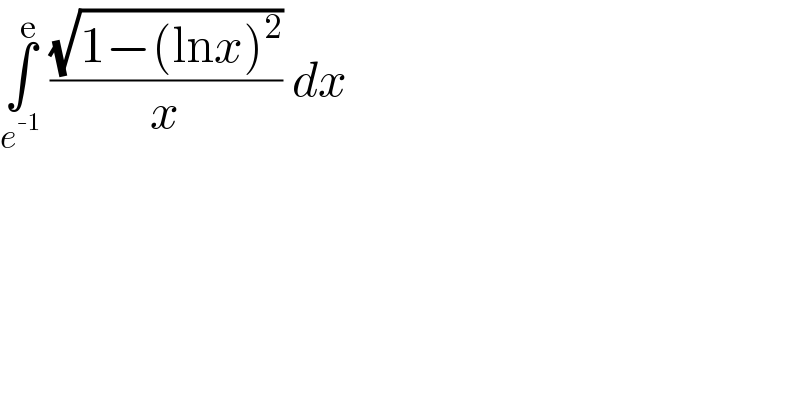 | ||
Commented by ajfour last updated on 04/Apr/20 | ||
![let ln x=t ⇒ (dx)/x=dt I=2∫_0 ^( 1) (√(1−t^2 )) dt = [t(√(1−t^2 ))+sin^(−1) t ]_0 ^1 = π/2 .](Q87463.png) | ||
Answered by Ar Brandon last updated on 04/Apr/20 | ||
![Let x=e^y ⇒dx=e^y dy I=∫_(−1) ^1 ((√(1−y^2 ))/e^y )∙e^y dy= ∫_(−1) ^1 (√(1−y^2 ))dy I=(√(1−y^2 ))∫_(−1) ^1 dy−∫_(−1) ^1 [(d/dy)((√(1−y^2 )))∫dy]dy =[y(√(1−y^2 ))]_(−1) ^1 +∫_(−1) ^1 [(y^2 /(√(1−y^2 )))]dy let y=sin θ ⇒dy=cos θdθ I=∫_(−(π/2)) ^(π/2) sin^2 θ dθ=(1/2)∫_(−(π/2)) ^(π/2) (1−cos(2θ))dθ I=(1/2)[θ−(1/2)sin(2θ)]_(−(π/2)) ^(π/2) I=(1/2)[(π/2)+(π/2)]=(π/2)](Q87465.png) | ||
| ||