Question Number 87625 by M±th+et£s last updated on 05/Apr/20
![if f(x)=sin^(−1) (cos[x]) find Df and Rf the function notice/ [...] is floor](Q87625.png)
$${if}\:{f}\left({x}\right)={sin}^{−\mathrm{1}} \left({cos}\left[{x}\right]\right) \\ $$$${find}\:{Df}\:{and}\:\:{Rf}\:{the}\:{function} \\ $$$$ \\ $$$${notice}/\:\left[...\right]\:{is}\:{floor} \\ $$
Answered by mind is power last updated on 05/Apr/20
![sin^− is defind over/[−1,1] vos[x]∈[−1,1] f is defind over R cos(n) is dense in [−1,1] ⇒Rf =]−(π/2);(π/2)[](Q87659.png)
$${sin}^{−} \:\:{is}\:{defind}\:{over}/\left[−\mathrm{1},\mathrm{1}\right] \\ $$$${vos}\left[{x}\right]\in\left[−\mathrm{1},\mathrm{1}\right]\:{f}\:{is}\:{defind}\:{over}\:\mathbb{R} \\ $$$${cos}\left({n}\right)\:{is}\:{dense}\:{in}\:\left[−\mathrm{1},\mathrm{1}\right]\: \\ $$$$\left.\Rightarrow{Rf}\:=\right]−\frac{\pi}{\mathrm{2}};\frac{\pi}{\mathrm{2}}\left[\right. \\ $$
Commented by M±th+et£s last updated on 05/Apr/20
$${thank}\:{you}\:{sir} \\ $$
Commented by mind is power last updated on 05/Apr/20
$${can}\:{you}\:{sir}\:{pleasr}\:{repost}?\int\frac{{dx}}{\left(\left({x}+\mathrm{1}\right)....\left({x}+{n}\right)\right)^{\mathrm{2}} } \\ $$$$ \\ $$
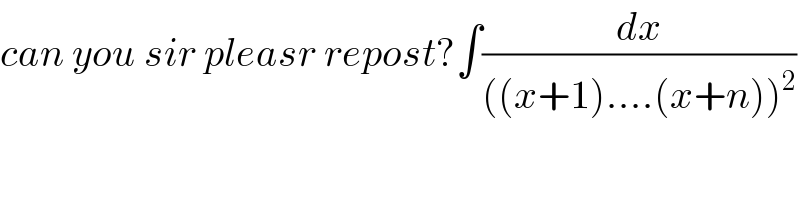
Answered by mr W last updated on 06/Apr/20
![i′ll try to answer the second part of the question: range of the function=? sin^(−1) (cos [x])=y acc. to definition: −(π/2)≤y≤(π/2) ⇒cos [x]=sin y=cos ((π/2)−y) ⇒[x]=2nπ±((π/2)−y)=m ⇒y=(π/2)±(m−2nπ) ⇒−(π/2)≤(π/2)±(m−2nπ)≤(π/2) ⇒−π≤±(m−2nπ)≤0 ⇒(2n−1)π≤m≤2nπ ⇒⌈(2n−1)π⌉≤m≤⌊2nπ⌋ ⇒0≤m−2nπ≤π ⇒2nπ≤m≤(2n+1)π ⇒⌈2nπ⌉≤m≤⌊(2n+1)π⌋ ⇒y=(π/2)+m−2nπ with ⌈(2n−1)π⌉≤m≤⌊2nπ⌋ ⇒y=(π/2)−m+2nπ with ⌈2nπ⌉≤m≤⌊(2n+1)π⌋](Q87807.png)
$${i}'{ll}\:{try}\:{to}\:{answer}\:{the}\:{second}\:{part}\:{of}\:{the} \\ $$$${question}:\:{range}\:{of}\:{the}\:{function}=? \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{cos}\:\left[{x}\right]\right)={y} \\ $$$${acc}.\:{to}\:{definition}:\:−\frac{\pi}{\mathrm{2}}\leqslant{y}\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}\:\left[{x}\right]=\mathrm{sin}\:{y}=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−{y}\right) \\ $$$$\Rightarrow\left[{x}\right]=\mathrm{2}{n}\pi\pm\left(\frac{\pi}{\mathrm{2}}−{y}\right)={m} \\ $$$$\Rightarrow{y}=\frac{\pi}{\mathrm{2}}\pm\left({m}−\mathrm{2}{n}\pi\right) \\ $$$$\Rightarrow−\frac{\pi}{\mathrm{2}}\leqslant\frac{\pi}{\mathrm{2}}\pm\left({m}−\mathrm{2}{n}\pi\right)\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow−\pi\leqslant\pm\left({m}−\mathrm{2}{n}\pi\right)\leqslant\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow\left(\mathrm{2}{n}−\mathrm{1}\right)\pi\leqslant{m}\leqslant\mathrm{2}{n}\pi \\ $$$$\Rightarrow\lceil\left(\mathrm{2}{n}−\mathrm{1}\right)\pi\rceil\leqslant{m}\leqslant\lfloor\mathrm{2}{n}\pi\rfloor \\ $$$$ \\ $$$$\Rightarrow\mathrm{0}\leqslant{m}−\mathrm{2}{n}\pi\leqslant\pi \\ $$$$\Rightarrow\mathrm{2}{n}\pi\leqslant{m}\leqslant\left(\mathrm{2}{n}+\mathrm{1}\right)\pi \\ $$$$\Rightarrow\lceil\mathrm{2}{n}\pi\rceil\leqslant{m}\leqslant\lfloor\left(\mathrm{2}{n}+\mathrm{1}\right)\pi\rfloor \\ $$$$ \\ $$$$\Rightarrow{y}=\frac{\pi}{\mathrm{2}}+{m}−\mathrm{2}{n}\pi\:{with}\:\lceil\left(\mathrm{2}{n}−\mathrm{1}\right)\pi\rceil\leqslant{m}\leqslant\lfloor\mathrm{2}{n}\pi\rfloor \\ $$$$\Rightarrow{y}=\frac{\pi}{\mathrm{2}}−{m}+\mathrm{2}{n}\pi\:{with}\:\lceil\mathrm{2}{n}\pi\rceil\leqslant{m}\leqslant\lfloor\left(\mathrm{2}{n}+\mathrm{1}\right)\pi\rfloor \\ $$
Commented by M±th+et£s last updated on 06/Apr/20
$${god}\:{bless}\:{you}\:{sir} \\ $$