Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 87648 by john santu last updated on 05/Apr/20

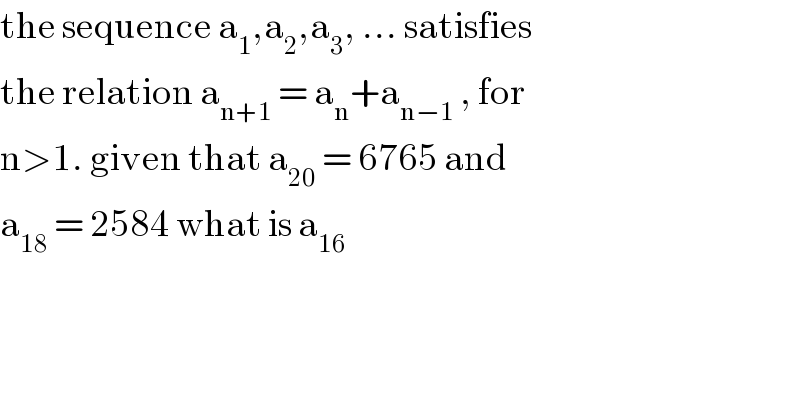
the sequence a_1 ,a_2 ,a_3 , ... satisfies the relation a_(n+1) = a_n +a_(n−1) , for n>1. given that a_(20) = 6765 and a_(18) = 2584 what is a_(16)

$$\mathrm{the}\:\mathrm{sequence}\:\mathrm{a}_{\mathrm{1}} ,\mathrm{a}_{\mathrm{2}} ,\mathrm{a}_{\mathrm{3}} ,\:...\:\mathrm{satisfies} \\ $$ $$\mathrm{the}\:\mathrm{relation}\:\mathrm{a}_{\mathrm{n}+\mathrm{1}} \:=\:\mathrm{a}_{\mathrm{n}} +\mathrm{a}_{\mathrm{n}−\mathrm{1}} \:,\:\mathrm{for} \\ $$ $$\mathrm{n}>\mathrm{1}.\:\mathrm{given}\:\mathrm{that}\:\mathrm{a}_{\mathrm{20}} \:=\:\mathrm{6765}\:\mathrm{and} \\ $$ $$\mathrm{a}_{\mathrm{18}} \:=\:\mathrm{2584}\:\mathrm{what}\:\mathrm{is}\:\mathrm{a}_{\mathrm{16}} \\ $$

Commented byjohn santu last updated on 05/Apr/20

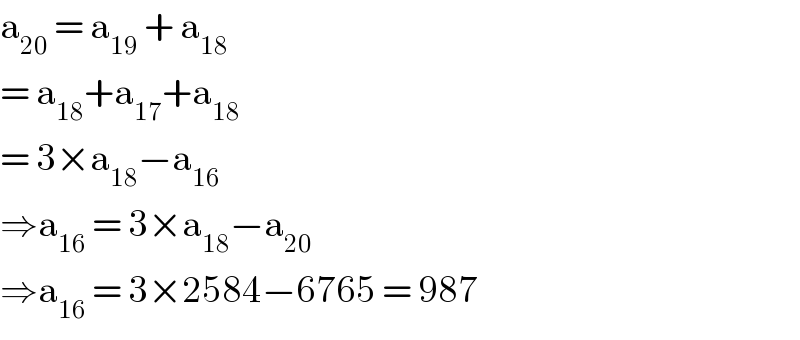
a_(20) = a_(19) + a_(18) = a_(18) +a_(17) +a_(18) = 3×a_(18) −a_(16) ⇒a_(16) = 3×a_(18) −a_(20) ⇒a_(16) = 3×2584−6765 = 987

$$\mathrm{a}_{\mathrm{20}} \:=\:\mathrm{a}_{\mathrm{19}} \:+\:\mathrm{a}_{\mathrm{18}} \\ $$ $$=\:\mathrm{a}_{\mathrm{18}} +\mathrm{a}_{\mathrm{17}} +\mathrm{a}_{\mathrm{18}} \\ $$ $$=\:\mathrm{3}×\mathrm{a}_{\mathrm{18}} −\mathrm{a}_{\mathrm{16}} \\ $$ $$\Rightarrow\mathrm{a}_{\mathrm{16}} \:=\:\mathrm{3}×\mathrm{a}_{\mathrm{18}} −\mathrm{a}_{\mathrm{20}} \\ $$ $$\Rightarrow\mathrm{a}_{\mathrm{16}} \:=\:\mathrm{3}×\mathrm{2584}−\mathrm{6765}\:=\:\mathrm{987} \\ $$

Commented byjohn santu last updated on 05/Apr/20

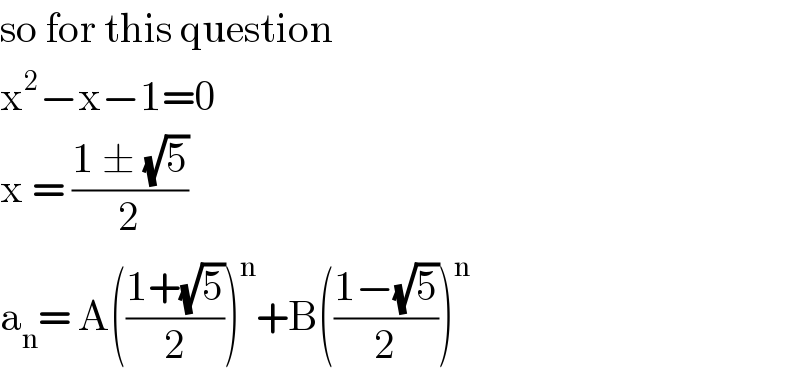
so for this question x^2 −x−1=0 x = ((1 ± (√5))/2) a_n = A(((1+(√5))/2))^n +B(((1−(√5))/2))^n

$$\mathrm{so}\:\mathrm{for}\:\mathrm{this}\:\mathrm{question}\: \\ $$ $$\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$ $$\mathrm{x}\:=\:\frac{\mathrm{1}\:\pm\:\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$ $$\mathrm{a}_{\mathrm{n}} =\:\mathrm{A}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}} +\mathrm{B}\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}} \\ $$

Commented bymr W last updated on 05/Apr/20

yes

$${yes} \\ $$

Commented byjohn santu last updated on 05/Apr/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com