
Question and Answers Forum
Question Number 87839 by jagoll last updated on 06/Apr/20
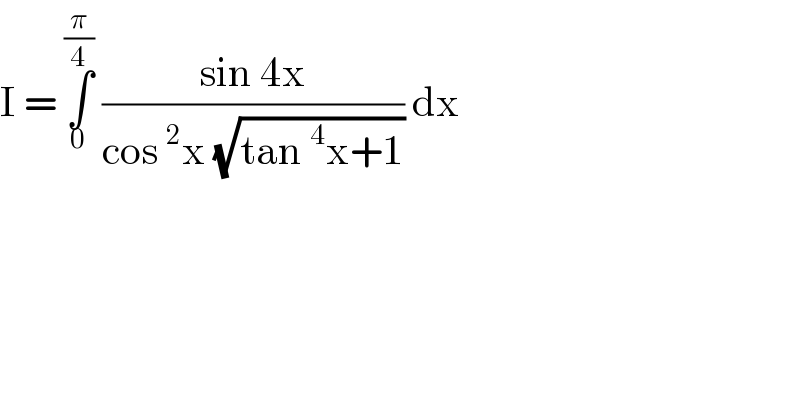
Answered by redmiiuser last updated on 06/Apr/20
![(√(tan^4 x+1)) =(√(sin^4 x+cos^4 x))/cos^2 x ((sin 4x)/(√(sin^4 x+cos^4 x))) =((sin 4x)/(√((3+cos 4x)/4))) ∫_0 ^(π/4) ((2sin 4x)/(√(3+cos 4x)))dx 3+cos 4x=z dz=4.sin 4x.dx ∫_4 ^2 ((2.dz)/(4.(√z))) =(1/2)∫_4 ^2 (dz/(√z)) =[(√z)]_4 ^2 =(√2)−2](Q87851.png)
Commented by jagoll last updated on 06/Apr/20
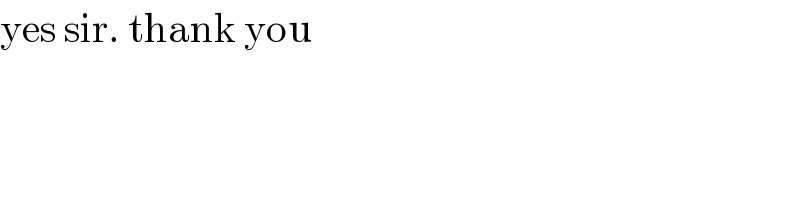
| ||
Question and Answers Forum | ||
Question Number 87839 by jagoll last updated on 06/Apr/20 | ||
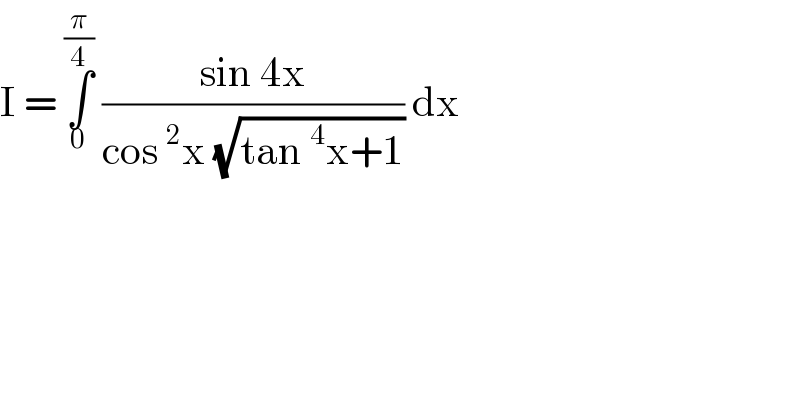 | ||
Answered by redmiiuser last updated on 06/Apr/20 | ||
![(√(tan^4 x+1)) =(√(sin^4 x+cos^4 x))/cos^2 x ((sin 4x)/(√(sin^4 x+cos^4 x))) =((sin 4x)/(√((3+cos 4x)/4))) ∫_0 ^(π/4) ((2sin 4x)/(√(3+cos 4x)))dx 3+cos 4x=z dz=4.sin 4x.dx ∫_4 ^2 ((2.dz)/(4.(√z))) =(1/2)∫_4 ^2 (dz/(√z)) =[(√z)]_4 ^2 =(√2)−2](Q87851.png) | ||
| ||
Commented by jagoll last updated on 06/Apr/20 | ||
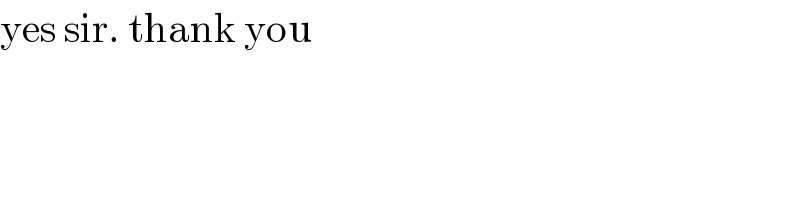 | ||