
Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 87905 by john santu last updated on 07/Apr/20

Commented by john santu last updated on 07/Apr/20
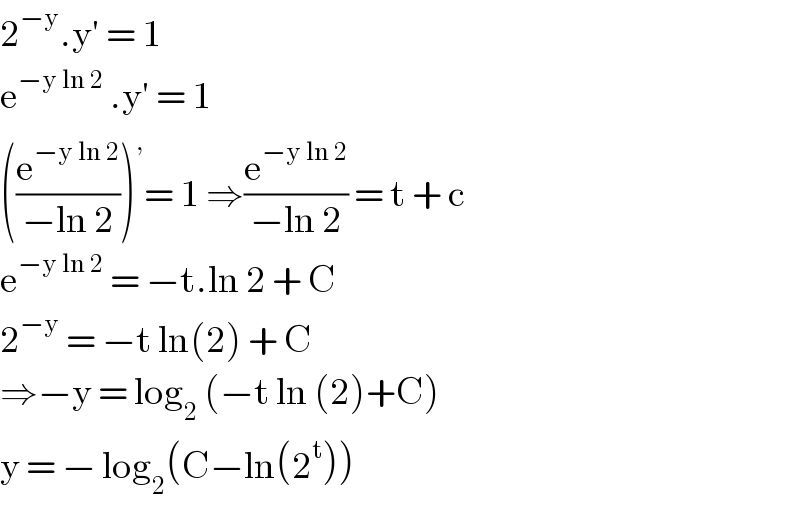
Answered by Joel578 last updated on 07/Apr/20
![(dy/dx) = 2^y ⇒ ∫ 2^(−y) dy = ∫ dx ⇒ −(2^(−y) /(ln 2)) = x + C_1 ⇒ 2^(−y) = (C_2 − x)ln 2 , C_2 = −C_1 ⇒ −y ln 2 = ln [(C_2 − x)ln 2] ⇒ y(x) = −((ln [(C_2 − x)ln 2])/(ln 2)) = − log_2 [(C_2 − x)ln 2]](Q87909.png)
| ||
Question and Answers Forum | ||
Previous in Differential Equation Next in Differential Equation | ||
Question Number 87905 by john santu last updated on 07/Apr/20 | ||
 | ||
Commented by john santu last updated on 07/Apr/20 | ||
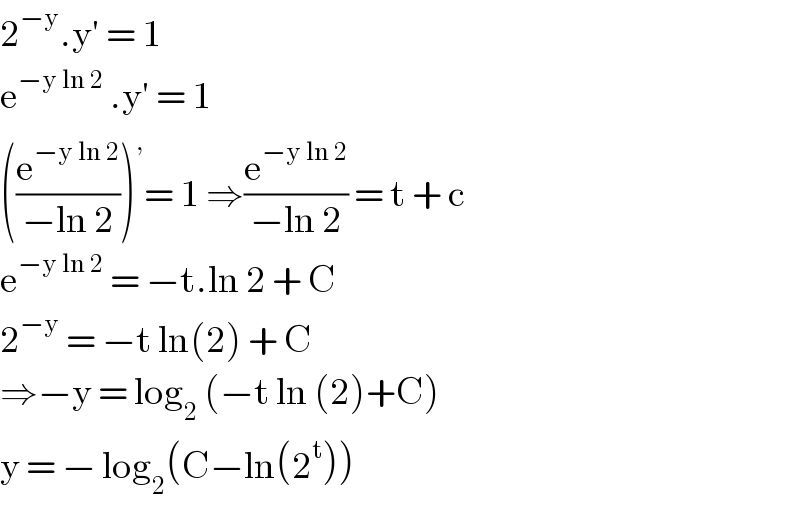 | ||
Answered by Joel578 last updated on 07/Apr/20 | ||
![(dy/dx) = 2^y ⇒ ∫ 2^(−y) dy = ∫ dx ⇒ −(2^(−y) /(ln 2)) = x + C_1 ⇒ 2^(−y) = (C_2 − x)ln 2 , C_2 = −C_1 ⇒ −y ln 2 = ln [(C_2 − x)ln 2] ⇒ y(x) = −((ln [(C_2 − x)ln 2])/(ln 2)) = − log_2 [(C_2 − x)ln 2]](Q87909.png) | ||
| ||