
Question and Answers Forum
Question Number 88065 by arcana last updated on 08/Apr/20
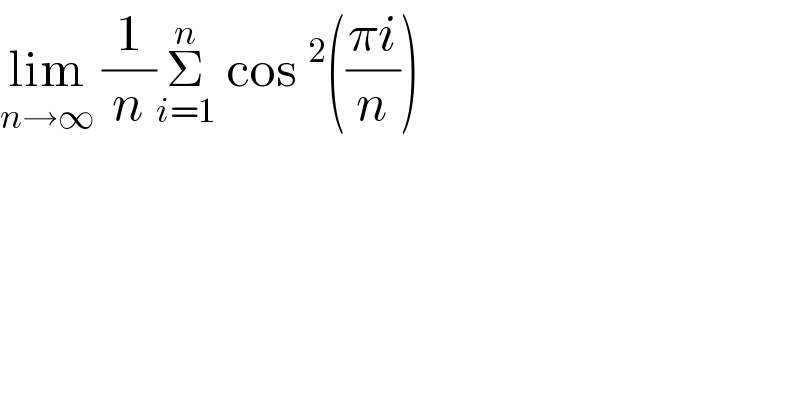
Commented by mathmax by abdo last updated on 08/Apr/20
![∫_a ^b f(x)dx =lim_(n→+∞) ((b−a)/n)Σ_(k=1) ^n f(a+((k(b−a))/n)) (Rieman sum) ⇒ lim_(n→∞) (1/n)Σ_(i=1) ^n cos^2 (((iπ)/n)) =(1/π)lim_(n→+∞) ((π−0)/n)Σ_(i=1) ^n cos^2 (((i(π−0))/n)) =(1/π)∫_0 ^π cos^2 x dx =(1/(2π))∫_0 ^π (1+cos(2x))dx =(1/2) +(1/(4π))[sin(2x)]_0 ^π =(1/2)](Q88156.png)
Commented by arcana last updated on 08/Apr/20

Commented by abdomathmax last updated on 10/Apr/20

| ||
Question and Answers Forum | ||
Question Number 88065 by arcana last updated on 08/Apr/20 | ||
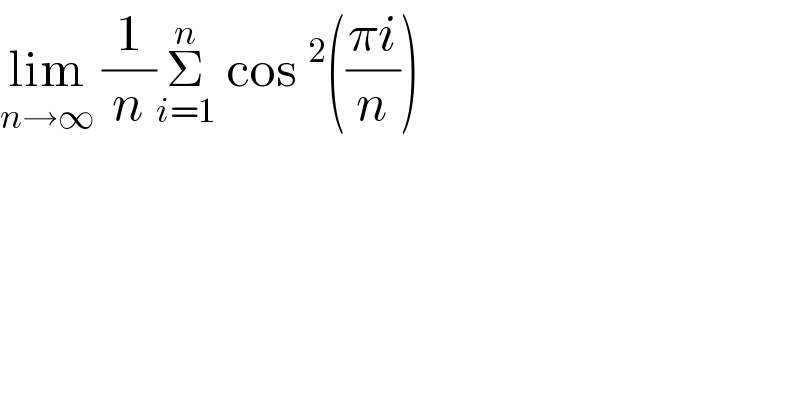 | ||
Commented by mathmax by abdo last updated on 08/Apr/20 | ||
![∫_a ^b f(x)dx =lim_(n→+∞) ((b−a)/n)Σ_(k=1) ^n f(a+((k(b−a))/n)) (Rieman sum) ⇒ lim_(n→∞) (1/n)Σ_(i=1) ^n cos^2 (((iπ)/n)) =(1/π)lim_(n→+∞) ((π−0)/n)Σ_(i=1) ^n cos^2 (((i(π−0))/n)) =(1/π)∫_0 ^π cos^2 x dx =(1/(2π))∫_0 ^π (1+cos(2x))dx =(1/2) +(1/(4π))[sin(2x)]_0 ^π =(1/2)](Q88156.png) | ||
Commented by arcana last updated on 08/Apr/20 | ||
 | ||
Commented by abdomathmax last updated on 10/Apr/20 | ||
 | ||