
Question and Answers Forum
Question Number 88169 by jagoll last updated on 08/Apr/20

Commented by mathmax by abdo last updated on 08/Apr/20
![L(x^3 cos(4x))=∫_0 ^∞ f(t) e^(−xt) dt =∫_0 ^∞ t^3 cos(4t)e^(−xt) dt =Re(∫_0 ^∞ t^3 e^(i4t−xt) dt) ∫_0 ^∞ t^3 e^((−x+4i)t) dt =_(bypsrts) [(t^3 /(−x+4i)) e^((−x+4i)t) ]_0 ^∞ −(1/(−x+4i))∫_0 ^∞ 3t^2 e^((−x+4i)t) dt =(3/(x−4i)) { [(t^2 /(−x+4i)) e^((−x+4i)t) ]_0 ^∞ −(1/(−x+4i))∫_0 ^∞ 2t e^((−x+4i)t) dt} =(6/((x−4i)^2 )) ∫_0 ^∞ t e^((−x+4i)t) dt =(6/((x−4i)^2 )){ [−(t/(−x+4i)) e^((−x+4i)t) ]_0 ^∞ −(1/(−x+4i))∫_0 ^∞ e^((−x+4i)t) dt} =(6/((x−4i)^3 ))[(1/(−x+4i)) e^((−x+4i)t) ]_0 ^∞ =(6/((x−4i)^4 )) =6((1/(x−4i)))^4 =6(((x+4i)/(x^2 +16)))^4 =(6/(x^2 +16))(x+4i)^2 (x+4i)^2 =(6/(x^2 +16))(x^2 +8ix −16)^2 =(6/(x^2 +16)){ (x^2 +8ix)^2 −32(x^2 +8ix)+16^2 } =(6/(x^2 +16)){ x^4 +16ix^3 −64 x^2 −32x^2 −8.32ix +16^2 } ⇒ L(x^3 (4x)) =(6/(x^2 +16))( x^4 −96x^2 +16^2 )](Q88195.png)
Commented by mathmax by abdo last updated on 09/Apr/20
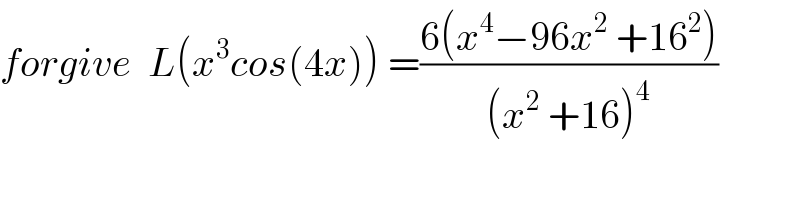
Answered by jagoll last updated on 09/Apr/20
![L(cos 4t) = (s/(s^2 +16)) L(t cos 4t) = −(d/ds)[(s/(s^2 +16))] = ((16−s^2 )/((s^2 +16)^2 )) L(t^2 cos 4t) = −(d/ds)[((16−s^2 )/((s^2 +16)^2 ))] = ((96s−2s^3 )/((s^2 +16)^3 )) L(t^3 cos 4t) = −(d/ds)[((96s−2s^3 )/((s^2 +16)^3 ))] = ((6(s^4 −96s^2 +256))/((s^2 +16)^4 ))](Q88205.png)
| ||
Question and Answers Forum | ||
Question Number 88169 by jagoll last updated on 08/Apr/20 | ||
 | ||
Commented by mathmax by abdo last updated on 08/Apr/20 | ||
![L(x^3 cos(4x))=∫_0 ^∞ f(t) e^(−xt) dt =∫_0 ^∞ t^3 cos(4t)e^(−xt) dt =Re(∫_0 ^∞ t^3 e^(i4t−xt) dt) ∫_0 ^∞ t^3 e^((−x+4i)t) dt =_(bypsrts) [(t^3 /(−x+4i)) e^((−x+4i)t) ]_0 ^∞ −(1/(−x+4i))∫_0 ^∞ 3t^2 e^((−x+4i)t) dt =(3/(x−4i)) { [(t^2 /(−x+4i)) e^((−x+4i)t) ]_0 ^∞ −(1/(−x+4i))∫_0 ^∞ 2t e^((−x+4i)t) dt} =(6/((x−4i)^2 )) ∫_0 ^∞ t e^((−x+4i)t) dt =(6/((x−4i)^2 )){ [−(t/(−x+4i)) e^((−x+4i)t) ]_0 ^∞ −(1/(−x+4i))∫_0 ^∞ e^((−x+4i)t) dt} =(6/((x−4i)^3 ))[(1/(−x+4i)) e^((−x+4i)t) ]_0 ^∞ =(6/((x−4i)^4 )) =6((1/(x−4i)))^4 =6(((x+4i)/(x^2 +16)))^4 =(6/(x^2 +16))(x+4i)^2 (x+4i)^2 =(6/(x^2 +16))(x^2 +8ix −16)^2 =(6/(x^2 +16)){ (x^2 +8ix)^2 −32(x^2 +8ix)+16^2 } =(6/(x^2 +16)){ x^4 +16ix^3 −64 x^2 −32x^2 −8.32ix +16^2 } ⇒ L(x^3 (4x)) =(6/(x^2 +16))( x^4 −96x^2 +16^2 )](Q88195.png) | ||
Commented by mathmax by abdo last updated on 09/Apr/20 | ||
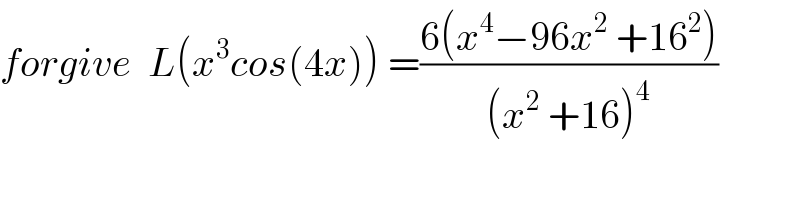 | ||
Answered by jagoll last updated on 09/Apr/20 | ||
![L(cos 4t) = (s/(s^2 +16)) L(t cos 4t) = −(d/ds)[(s/(s^2 +16))] = ((16−s^2 )/((s^2 +16)^2 )) L(t^2 cos 4t) = −(d/ds)[((16−s^2 )/((s^2 +16)^2 ))] = ((96s−2s^3 )/((s^2 +16)^3 )) L(t^3 cos 4t) = −(d/ds)[((96s−2s^3 )/((s^2 +16)^3 ))] = ((6(s^4 −96s^2 +256))/((s^2 +16)^4 ))](Q88205.png) | ||
| ||