
Question and Answers Forum
Question Number 88206 by jagoll last updated on 09/Apr/20
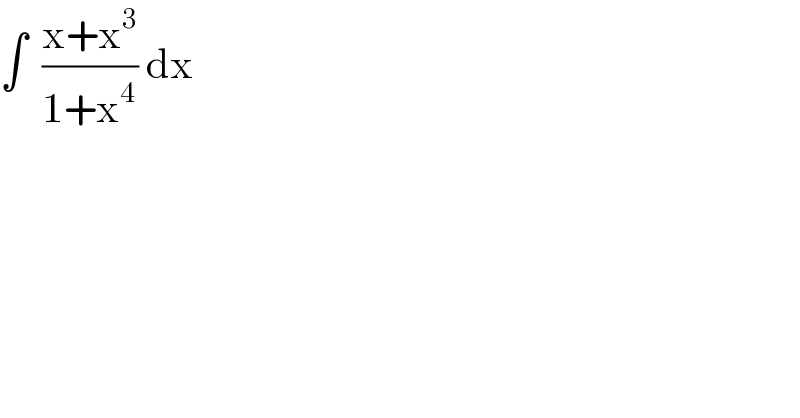
Answered by john santu last updated on 09/Apr/20
![= ∫ (x/(1+x^4 )) dx + ∫ (x^3 /(1+x^4 )) dx = (1/2)∫ ((2x)/(1+x^4 )) dx + (1/4)∫ ((4x^3 )/(1+x^4 )) dx = (1/2) ∫ ((d(x^2 ))/(1+(x^2 )^2 )) + (1/4)∫ ((d(1+x^4 ))/(1+x^4 )) = (1/4) ln (1+x^4 ) + (1/2)∫ (du/(1+u^2 )) , [ u =x^2 ] = (1/4)ln(1+x^4 ) +(1/2)arc tan (x^2 ) + c](Q88208.png)
Commented by jagoll last updated on 09/Apr/20

| ||
Question and Answers Forum | ||
Question Number 88206 by jagoll last updated on 09/Apr/20 | ||
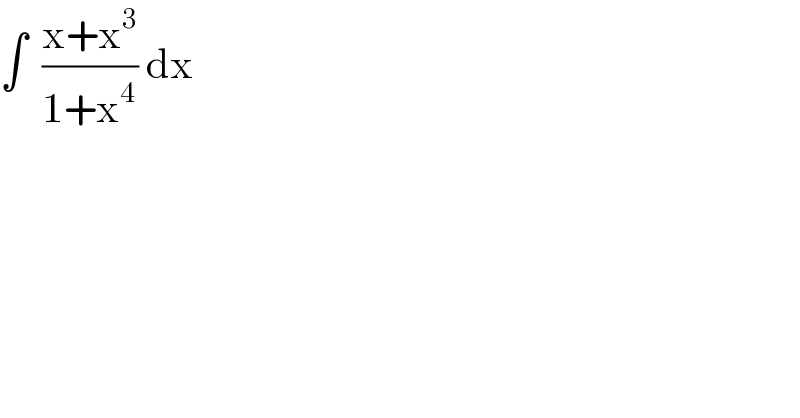 | ||
Answered by john santu last updated on 09/Apr/20 | ||
![= ∫ (x/(1+x^4 )) dx + ∫ (x^3 /(1+x^4 )) dx = (1/2)∫ ((2x)/(1+x^4 )) dx + (1/4)∫ ((4x^3 )/(1+x^4 )) dx = (1/2) ∫ ((d(x^2 ))/(1+(x^2 )^2 )) + (1/4)∫ ((d(1+x^4 ))/(1+x^4 )) = (1/4) ln (1+x^4 ) + (1/2)∫ (du/(1+u^2 )) , [ u =x^2 ] = (1/4)ln(1+x^4 ) +(1/2)arc tan (x^2 ) + c](Q88208.png) | ||
| ||
Commented by jagoll last updated on 09/Apr/20 | ||
 | ||