prove that ∣((e^z −e^(−z) )/2)∣^2 +cos^2 y=sinh^2 x when z=x+iy


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 88263 by M±th+et£s last updated on 09/Apr/20

$p r o v e t h a t$ $∣ \frac{e^{z} - e^{- z}}{2} ∣^{2} + {c o s}^{2} y = {s i n h}^{2} x w h e n z = x + i y$
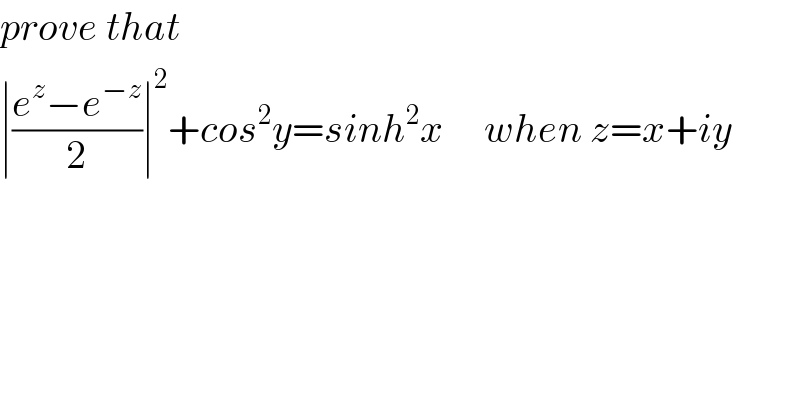
Commented by M±th+et£s last updated on 09/Apr/20

$p l e a s e h e l p$
	Answered by TANMAY PANACEA. last updated on 09/Apr/20

	$e^{x + i y} = e^{x} . e^{i y} = (c o s h x + s i n h x) (c o s y + i s i n y)$ $= c o s h x c o s y + i c o s h x s i n y + s i n h x c o s y + i s i n h x s i n y$ $= c o s y (c o s h x + s i n h x) + i s i n y (c o s h x + s i n h x)$ $e^{- (x + i y)} = e^{- x} . e^{- i y} = (c o s h x - s i n h x) (c o s y - i s i n y)$ $= c o s h x c o s y - i c o s h x s i n y - s i n h x c o s y + i s i n h x s i n y$ $= c o s y (c o s h x - s i n h x) - i s i n y (c o s h x - s i n h x)$ $n o w$ $\frac{e^{z} - e^{- z}}{2} = \frac{1}{2} [c o s y (2 s i n h x) + i s i n y (2 c o s h x)]$ $∣ \frac{e^{z} - e^{- z}}{2} ∣^{2} = {(c o s y s i n h x)}^{2} + {(s i n y c o s h x)}^{2}$ ${c o s}^{2} y {(s i n h x)}^{2} + {s i n}^{2} y {(c o s h x)}^{2} + {c o s}^{2} y$ $= {c o s}^{2} y [1 + {(s i n h x)}^{2}] + {s i n}^{2} y {(c o s h x)}^{2}$ $= {c o s}^{2} y [{c o s}^{2} h x - {s i n}^{2} h x + {s i n}^{2} h x] + {s i n}^{2} {y c o s}^{2} h x$ $= ({c o s}^{2} y + {s i n}^{2} y) {c o s}^{2} h x$ $= {c o s}^{2} h x$ $p l s c h e c k$
	Commented by M±th+et£s last updated on 09/Apr/20

	$y e s s i r i t s t y p o g o d b l e s s y o u$
	Commented by TANMAY PANACEA. last updated on 09/Apr/20

	$m o s t w e l c o m e s i r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum