
Question and Answers Forum
Question Number 88288 by Chi Mes Try last updated on 09/Apr/20
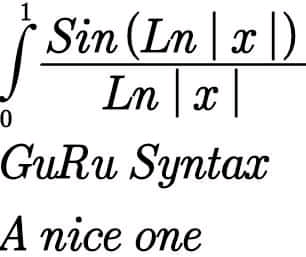
Commented by abdomathmax last updated on 10/Apr/20
![I =∫_0 ^1 ((sin(ln∣x∣))/(ln∣x∣))dx changement ln(x)=−u ⇒ I =∫_0 ^1 ((sin(lnx))/(lnx))dx =−∫_0 ^(+∞) ((−sinu)/(−u))(−e^(−u) )du = ∫_0 ^∞ ((sinu)/u) e^(−u) du let f(t) =∫_0 ^∞ ((sinu)/u)e^(−tu) du with t>0 f^′ (t) =−∫_0 ^∞ e^(−tu) sinu du =−Im(∫_0 ^∞ e^(−tu+iu) du) =−Im(∫_0 ^∞ e^((−t+i)u) du) ∫_0 ^∞ e^((−t+i)u) du =[(1/(−t+i))e^((−t+i)u) ]_0 ^(+∞) =((−1)/(−t+i)) =(1/(t−i)) =((t+i)/(t^2 +1)) ⇒f^′ (t)=−(1/(1+t^2 )) ⇒ f(t) =k−arctant lim_(t→0) f(t) =∫_0 ^∞ ((sinu)/u)du =(π/2)=k ⇒ f(t) =(π/2) −arcrant (t>0) I =f(1) =(π/2)−(π/4) =(π/4)](Q88334.png)
Answered by mind is power last updated on 09/Apr/20
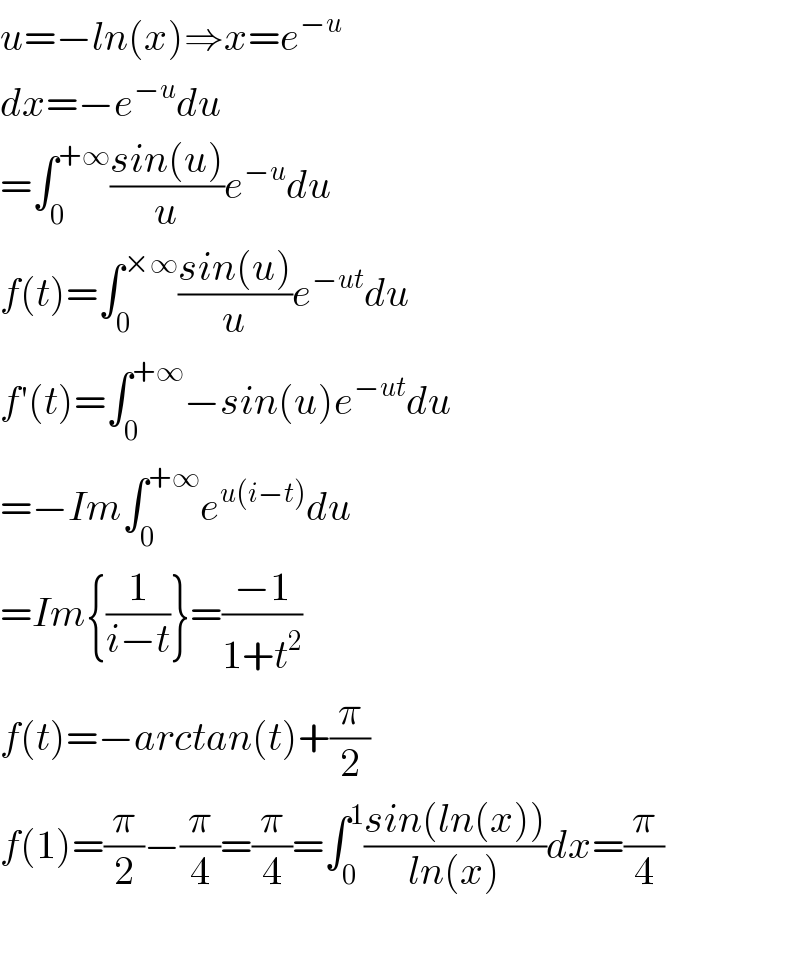
| ||
Question and Answers Forum | ||
Question Number 88288 by Chi Mes Try last updated on 09/Apr/20 | ||
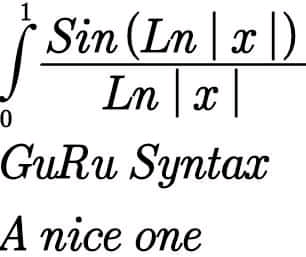 | ||
Commented by abdomathmax last updated on 10/Apr/20 | ||
![I =∫_0 ^1 ((sin(ln∣x∣))/(ln∣x∣))dx changement ln(x)=−u ⇒ I =∫_0 ^1 ((sin(lnx))/(lnx))dx =−∫_0 ^(+∞) ((−sinu)/(−u))(−e^(−u) )du = ∫_0 ^∞ ((sinu)/u) e^(−u) du let f(t) =∫_0 ^∞ ((sinu)/u)e^(−tu) du with t>0 f^′ (t) =−∫_0 ^∞ e^(−tu) sinu du =−Im(∫_0 ^∞ e^(−tu+iu) du) =−Im(∫_0 ^∞ e^((−t+i)u) du) ∫_0 ^∞ e^((−t+i)u) du =[(1/(−t+i))e^((−t+i)u) ]_0 ^(+∞) =((−1)/(−t+i)) =(1/(t−i)) =((t+i)/(t^2 +1)) ⇒f^′ (t)=−(1/(1+t^2 )) ⇒ f(t) =k−arctant lim_(t→0) f(t) =∫_0 ^∞ ((sinu)/u)du =(π/2)=k ⇒ f(t) =(π/2) −arcrant (t>0) I =f(1) =(π/2)−(π/4) =(π/4)](Q88334.png) | ||
Answered by mind is power last updated on 09/Apr/20 | ||
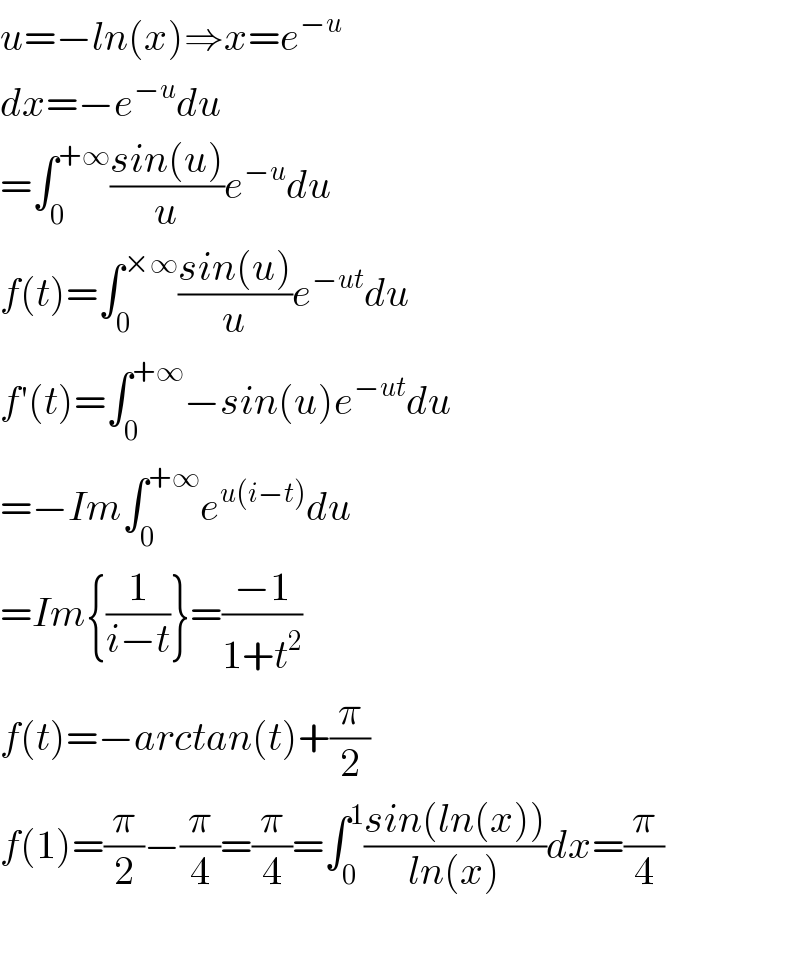 | ||
| ||