Question and Answers Forum
Question Number 88310 by ajfour last updated on 09/Apr/20
Commented by ajfour last updated on 09/Apr/20
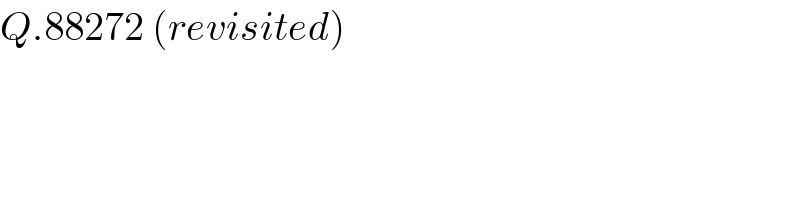
Answered by ajfour last updated on 10/Apr/20
![h^2 +k^2 =r^2 y^2 =b^2 (1−(((x−a)^2 )/a^2 )) [ellipse] x^2 +y^2 −2hx−2ky=0 [circle] (x^2 +y^2 −2hx)^2 =4(r^2 −h^2 )y^2 ⇒ {x^2 +b^2 (1−(((x−a)^2 )/a^2 ))−2hx}^2 = 4(r^2 −h^2 )b^2 (1−(((x−a)^2 )/a^2 )) roots of above eq. are x_1 =0 , x_2 =2h, x_3 =x_4 =t first we eliminate x=0, then determine h(r). then eliminate t and eventually find r. .... let (x/a)=X, (h/a)=s, (b^2 /a^2 )=q, (t/a)=m, (r/a)=R . {X^2 +q(2X−X^2 )−2sX}^2 = 4(R^2 −s^2 )q(2X−X^2 ) ⇒ X{X+q(2−X)−2s}^2 =4q(R^2 −s^2 )(2−X) roots are now X=2s, m,m. lets put X=2s ⇒qs(1−s)=(R^2 −s^2 ) ⇒ R^2 =(1−q)s^2 +qs ...(I) And R^2 −s^2 =qs(1−s) ...(II) now generally (1−q)^2 X^3 +4(1−q)(q−s)X^2 +4(q−s)^2 X +4q(R^2 −s^2 )X−8q(R^2 −s^2 )=0 ⇒ (1−q)^2 X^3 +4(1−q)(q−s)X^2 +4{(q−s)^2 +q(R^2 −s^2 )}X −8q(R^2 −s^2 )=0 2m+2s=−((4(q−s))/((1−q))) ...(i) 2m^2 s=((8q(R^2 −s^2 ))/((1−q)^2 )) ...(ii) ⇒ s{((2(s−q))/((1−q)))−s}^2 =((4q(R^2 −s^2 ))/((1−q)^2 )) now using (II) ⇒ s{((2(s−q))/((1−q)))−s}^2 =((4q(qs)(1−s))/((1−q)^2 )) ⇒ {((2(s−q))/((1−q)))−s}^2 =((4q^2 (1−s))/((1−q)^2 )) ⇒{(1+q)s−2q}^2 =4q^2 (1−s) (1+q)^2 s^2 −4qs=0 and as s≠0 s=((4q)/((1+q)^2 )) Now using (I) ⇒ R=(√((1−q)s^2 +qs )) ⇒ R = (√(((16(1−q)q^2 )/((1+q)^4 ))+((4q^2 )/((1+q)^2 )))) or R=((2q(√((1−q)^2 +4)))/((1+q)^2 )) for example if a=4, b=3 q=(9/(16)), R=((18(√(1073)))/(625)) ≈ 0.9434 ...](Q88312.png)
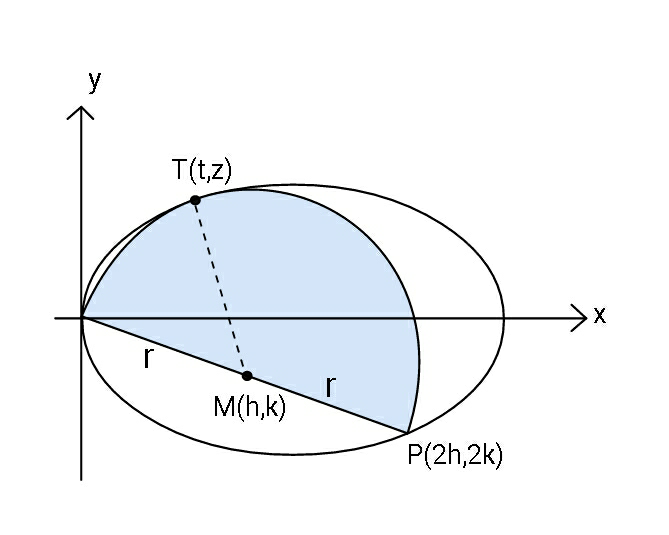
Commented by mr W last updated on 10/Apr/20
Commented by ajfour last updated on 10/Apr/20
Commented by mr W last updated on 09/Apr/20

Commented by ajfour last updated on 10/Apr/20
Commented by ajfour last updated on 10/Apr/20
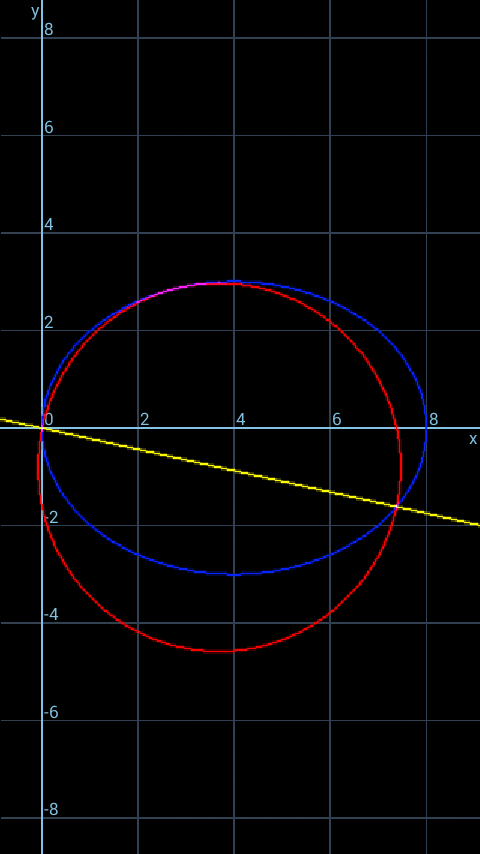
Commented by MJS last updated on 10/Apr/20
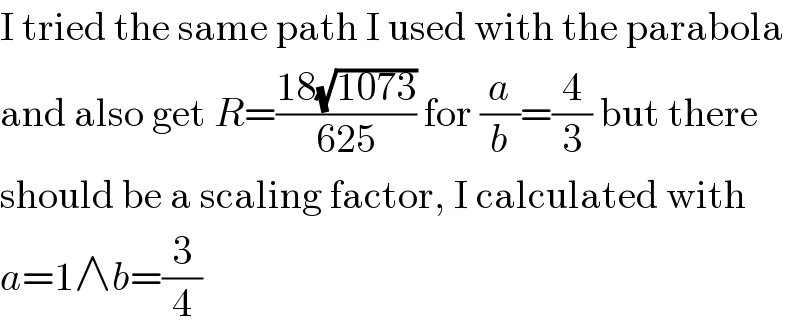
Commented by ajfour last updated on 10/Apr/20
Commented by mr W last updated on 10/Apr/20