
Question Number 88414 by abdomathmax last updated on 10/Apr/20
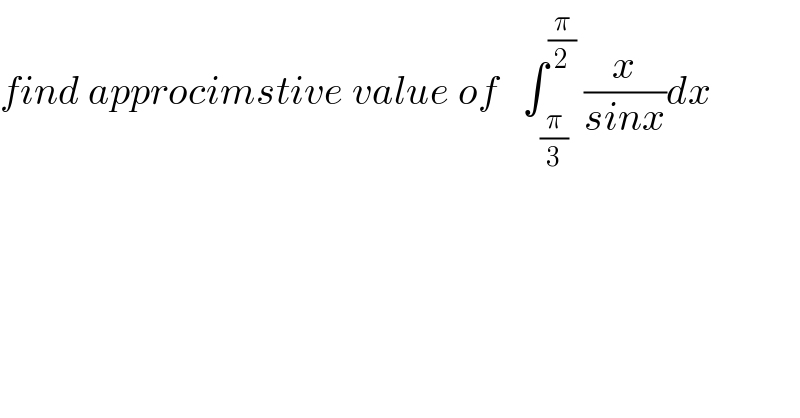
$${find}\:{approcimstive}\:{value}\:{of}\:\:\:\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{x}}{{sinx}}{dx} \\ $$
Commented by mathmax by abdo last updated on 12/Apr/20
![we have sinx =x−(x^3 /6) +....⇒x−(x^3 /6)≤sinx≤x ∀ x∈[(π/3),(π/2)] ⇒ (1/x)≤(1/(sinx))≤(1/(x−(x^3 /6))) ⇒ 1≤(x/(sinx))≤(1/(1−(x^2 /6))) ⇒ (π/2)−(π/3)≤∫_(π/3) ^(π/2) (x/(sinx))dx ≤ 6∫_(π/3) ^(π/2) (dx/(6−x^2 )) we have ∫_(π/3) ^(π/2) (dx/(6−x^2 )) =(1/(2(√6)))∫_(π/3) ^(π/2) ((1/((√6)−x))+(1/((√6)+x)))dx =(1/(2(√6)))[ln∣(((√6)+x)/((√6)−x))∣]_(π/3) ^(π/2) =(1/(2(√6))){ ln((((√6)+(π/2))/((√6)−(π/2))))−ln((((√6)+(π/3))/((√6)−(π/3))))} =(1/(2(√6))){ln(((2(√6)+π)/(2(√6)−π)))−ln(((3(√6)+π)/(3(√6)−π)))} ⇒ (π/6)≤∫_(π/3) ^(π/2) (x/(sinx))dx ≤((√6)/2){ ln(((2(√6)+π)/(2(√6)−π)))−ln(((3(√6)+π)/(3(√6)−π)))} we can take v_0 =(π/2) +((√6)/4){ ln(((2(√6)+π)/(2(√6)−π)))−ln(((3(√6)+π)/(3(√6)−π)))} as a approximste value](Q88665.png)
$${we}\:{have}\:{sinx}\:={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\:+....\Rightarrow{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\leqslant{sinx}\leqslant{x}\:\:\forall\:{x}\in\left[\frac{\pi}{\mathrm{3}},\frac{\pi}{\mathrm{2}}\right]\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{x}}\leqslant\frac{\mathrm{1}}{{sinx}}\leqslant\frac{\mathrm{1}}{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}\:\Rightarrow\:\mathrm{1}\leqslant\frac{{x}}{{sinx}}\leqslant\frac{\mathrm{1}}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}}\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}\leqslant\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{x}}{{sinx}}{dx}\:\leqslant\:\mathrm{6}\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\mathrm{6}−{x}^{\mathrm{2}} } \\ $$$${we}\:{have}\:\:\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\mathrm{6}−{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{6}}−{x}}+\frac{\mathrm{1}}{\sqrt{\mathrm{6}}+{x}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\left[{ln}\mid\frac{\sqrt{\mathrm{6}}+{x}}{\sqrt{\mathrm{6}}−{x}}\mid\right]_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\left\{\:{ln}\left(\frac{\sqrt{\mathrm{6}}+\frac{\pi}{\mathrm{2}}}{\sqrt{\mathrm{6}}−\frac{\pi}{\mathrm{2}}}\right)−{ln}\left(\frac{\sqrt{\mathrm{6}}+\frac{\pi}{\mathrm{3}}}{\sqrt{\mathrm{6}}−\frac{\pi}{\mathrm{3}}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\left\{{ln}\left(\frac{\mathrm{2}\sqrt{\mathrm{6}}+\pi}{\mathrm{2}\sqrt{\mathrm{6}}−\pi}\right)−{ln}\left(\frac{\mathrm{3}\sqrt{\mathrm{6}}+\pi}{\mathrm{3}\sqrt{\mathrm{6}}−\pi}\right)\right\}\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{6}}\leqslant\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{x}}{{sinx}}{dx}\:\leqslant\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\left\{\:{ln}\left(\frac{\mathrm{2}\sqrt{\mathrm{6}}+\pi}{\mathrm{2}\sqrt{\mathrm{6}}−\pi}\right)−{ln}\left(\frac{\mathrm{3}\sqrt{\mathrm{6}}+\pi}{\mathrm{3}\sqrt{\mathrm{6}}−\pi}\right)\right\}\:{we}\:{can}\:{take} \\ $$$${v}_{\mathrm{0}} =\frac{\pi}{\mathrm{2}}\:+\frac{\sqrt{\mathrm{6}}}{\mathrm{4}}\left\{\:{ln}\left(\frac{\mathrm{2}\sqrt{\mathrm{6}}+\pi}{\mathrm{2}\sqrt{\mathrm{6}}−\pi}\right)−{ln}\left(\frac{\mathrm{3}\sqrt{\mathrm{6}}+\pi}{\mathrm{3}\sqrt{\mathrm{6}}−\pi}\right)\right\}\:{as}\:{a}\:{approximste}\:{value} \\ $$
Commented by mathmax by abdo last updated on 12/Apr/20

$${v}_{\mathrm{0}} =\frac{\pi}{\mathrm{12}}\:+\frac{\sqrt{\mathrm{6}}}{\mathrm{4}}\left\{.....\right\} \\ $$
