
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 88424 by abdomathmax last updated on 10/Apr/20
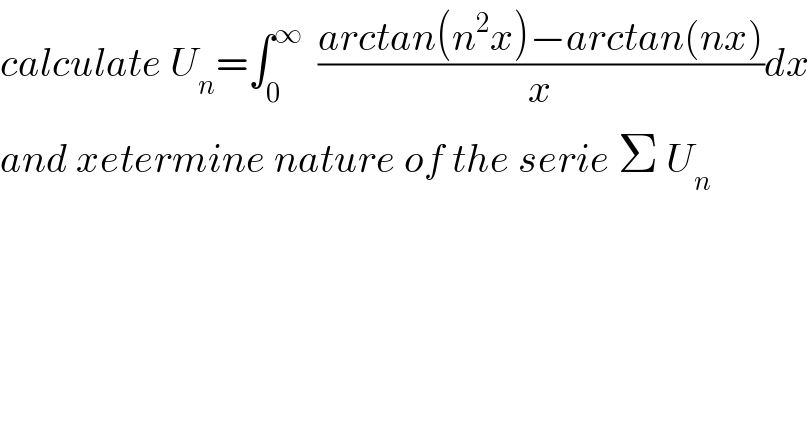
Commented by mathmax by abdo last updated on 11/Apr/20
![let I(ξ) =∫_0 ^ξ ((arctan(ax)−arctan(bx))/x)dx ⇒ I(ξ) =∫_0 ^ξ ((arctan(ax))/x)dx−∫_0 ^ξ ((arctan(bx))/x)dx but ∫_0 ^ξ ((arctan(ax))/x)dx =_(ax=t) ∫_0 ^(aξ) ((arctan(t))/(t/a))×(dt/a) =∫_0 ^(aξ) ((arctan(t))/t)dt also ∫_0 ^ξ ((arctan(bx))/x)dx =∫_0 ^(bξ) ((arctan(t))/t)dt ⇒ I(ξ) =∫_0 ^(aξ) ((arctant)/t)dt+∫_(bξ) ^0 ((arctan(t))/t)dt =∫_(bξ) ^(aξ) ((arctan(t))/t)dt ∃c ∈]bξ,aξ[ / I(ξ) =arctan(ξ)∫_(bξ) ^(aξ) (dt/t) =arctan(ξ)ln∣(a/b)∣ ⇒ lim_(ξ→+∞) I(ξ) =∫_0 ^∞ ((arctan(ax)−arctan(bx))/x)dx=(π/2)ln∣(a/b)∣ ⇒U_n =(π/2)arctan((n^2 /n)) =(π/2)arctan(n) we have lim_(n→+∞) U_n =(π^2 /4) ≠0 ⇒Σ U_n diverges](Q88576.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 88424 by abdomathmax last updated on 10/Apr/20 | ||
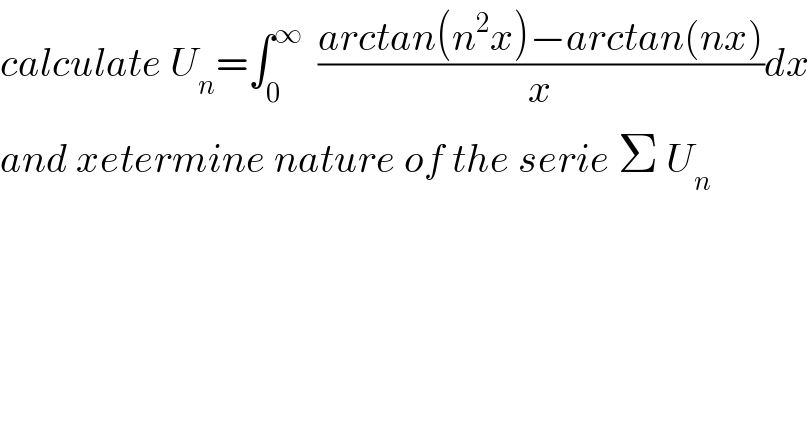 | ||
Commented by mathmax by abdo last updated on 11/Apr/20 | ||
![let I(ξ) =∫_0 ^ξ ((arctan(ax)−arctan(bx))/x)dx ⇒ I(ξ) =∫_0 ^ξ ((arctan(ax))/x)dx−∫_0 ^ξ ((arctan(bx))/x)dx but ∫_0 ^ξ ((arctan(ax))/x)dx =_(ax=t) ∫_0 ^(aξ) ((arctan(t))/(t/a))×(dt/a) =∫_0 ^(aξ) ((arctan(t))/t)dt also ∫_0 ^ξ ((arctan(bx))/x)dx =∫_0 ^(bξ) ((arctan(t))/t)dt ⇒ I(ξ) =∫_0 ^(aξ) ((arctant)/t)dt+∫_(bξ) ^0 ((arctan(t))/t)dt =∫_(bξ) ^(aξ) ((arctan(t))/t)dt ∃c ∈]bξ,aξ[ / I(ξ) =arctan(ξ)∫_(bξ) ^(aξ) (dt/t) =arctan(ξ)ln∣(a/b)∣ ⇒ lim_(ξ→+∞) I(ξ) =∫_0 ^∞ ((arctan(ax)−arctan(bx))/x)dx=(π/2)ln∣(a/b)∣ ⇒U_n =(π/2)arctan((n^2 /n)) =(π/2)arctan(n) we have lim_(n→+∞) U_n =(π^2 /4) ≠0 ⇒Σ U_n diverges](Q88576.png) | ||