
Question and Answers Forum
Question Number 88456 by ajfour last updated on 10/Apr/20

Commented by ajfour last updated on 11/Apr/20
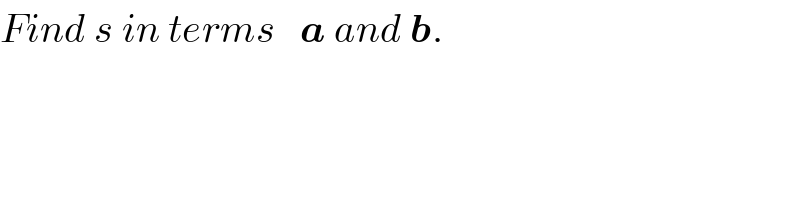
Commented by Tony Lin last updated on 11/Apr/20

Commented by Tony Lin last updated on 11/Apr/20
![k=scosθ,h=ssinθ [((cos(−60°)),(−sin(−60°))),((sin(−60°)),(cos(−60°))) ] [((−k)),(h) ] = [((((√3)h−k)/2)),((((√3)k+h)/2)) ] P=((((√3)h−k)/2)+k, (((√3)k+h)/2)) =((((√3)h+k)/2), (((√3)k+h)/2)) (x^2 /a^2 )+(y^2 /b^2 )=1 ((((((√3)h+k)/2))^2 )/a^2 )+((((((√3)k+h)/2))^2 )/b^2 )=1 k^2 (b^2 +3a^2 )+h^2 (a^2 +3b^2 )+2(√3)hk(a^2 +b^2 ) s^2 [cos^2 θ(b^2 +3a^2 )+sin^2 θ(a^2 +3b^2 )+(√3)sin2θ(a^2 +b^2 ) =4a^2 b^2 s=(√((4a^2 b^2 )/(cos^2 θ(b^2 +3a^2 )+sin^2 θ(a^2 +3b^2 )+(√3)sin2θ(a^2 +b^2 ))))](Q88520.png)
Commented by ajfour last updated on 11/Apr/20
Answered by mr W last updated on 11/Apr/20

Commented by mr W last updated on 11/Apr/20
![y_Q =s sin θ x_P =s cos ((π/3)−θ)=(s/2)(cos θ+(√3) sin θ) y_P =s[sin θ+sin ((π/3)−θ)]=(s/2)(sin θ+(√3) cos θ) b^2 x_P ^2 +a^2 y_P ^2 =a^2 b^2 (s^2 /4)[b^2 (cos θ+(√3) sin θ)^2 +a^2 (sin θ+(√3) cos θ)^2 ]=a^2 b^2 s^2 [b^2 (cos^2 θ+2(√3) sin θ cos θ+3 cos^2 θ)+a^2 (sin^2 θ+2(√3) sin θcos θ+3 sin^2 θ)]=4a^2 b^2 s^2 [(√3)(a^2 + b^2 ) sin 2θ+(a^2 +3b^2 ) sin^2 θ+(3a^2 +b^2 ) cos^2 θ)]=4a^2 b^2 with μ=(b/a) P=((4b^2 )/s^2 )=(√3)(1+ μ^2 ) sin 2θ+(1+3μ^2 ) sin^2 θ+(3+μ^2 ) cos^2 θ P=((4b^2 )/s^2 )=2(1+μ^2 )+(√3)(1+ μ^2 ) sin 2θ+(1−μ^2 )cos 2θ (dP/dθ)=2(√3)(1+ μ^2 ) cos 2θ−2(1−μ^2 ) sin 2θ=0 ⇒tan 2θ=(((1+μ^2 )(√3))/(1−μ^2 )) ⇒sin 2θ=(((1+μ^2 )(√3))/(2(√(1+μ^2 +μ^4 )))) ⇒cos 2θ=((1−μ^2 )/(2(√(1+μ^2 +μ^4 )))) ((4b^2 )/s_(min) ^2 )=2(1+μ^2 )+(√3)(1+ μ^2 )(((1+μ^2 )(√3))/(2(√(1+μ^2 +μ^4 ))))+(1−μ^2 )((1−μ^2 )/(2(√(1+μ^2 +μ^4 )))) ((2b^2 )/s_(min) ^2 )=1+μ^2 +(√(1+μ^2 +μ^4 )) ⇒s_(min) =(((√2)b)/(√(1+μ^2 +(√(1+μ^2 +μ^4 ))))) example: a=4, b=3, μ=(3/4) ⇒s_(min) =((√(50−2(√(481))))/3)×b=(√(50−2(√(481))))=2.477](Q88521.png)
Commented by ajfour last updated on 11/Apr/20
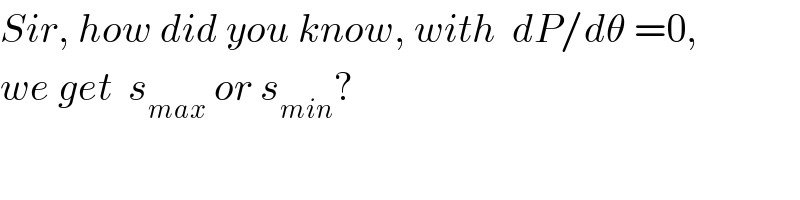
Commented by mr W last updated on 11/Apr/20

Commented by mr W last updated on 11/Apr/20

Commented by ajfour last updated on 11/Apr/20
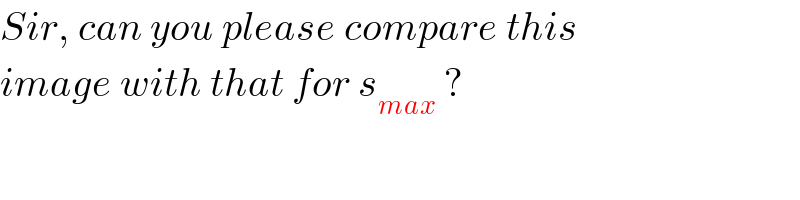
Commented by mr W last updated on 11/Apr/20
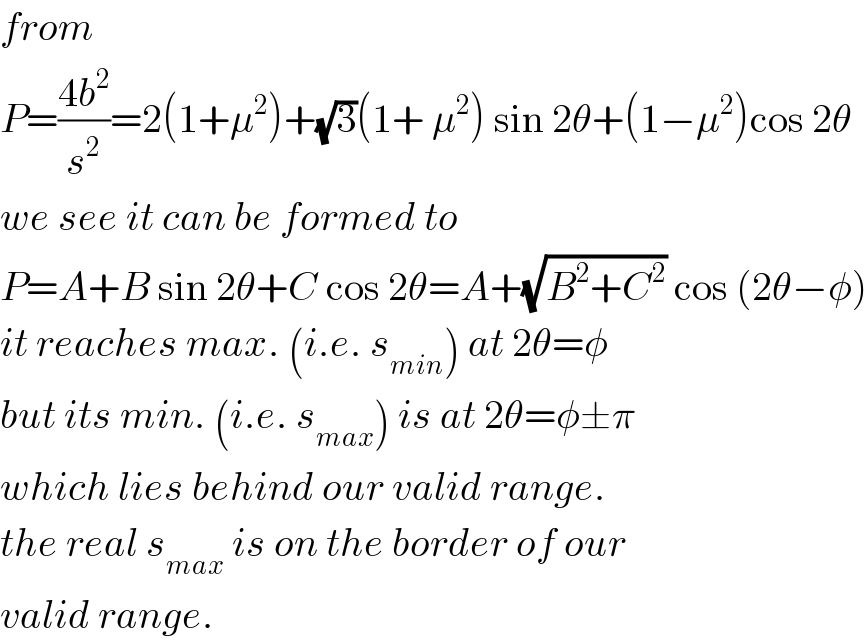
Commented by mr W last updated on 11/Apr/20

Commented by mr W last updated on 11/Apr/20

Commented by mr W last updated on 11/Apr/20

Commented by ajfour last updated on 11/Apr/20

