
Question and Answers Forum
Question Number 88491 by M±th+et£s last updated on 11/Apr/20

Answered by mr W last updated on 11/Apr/20
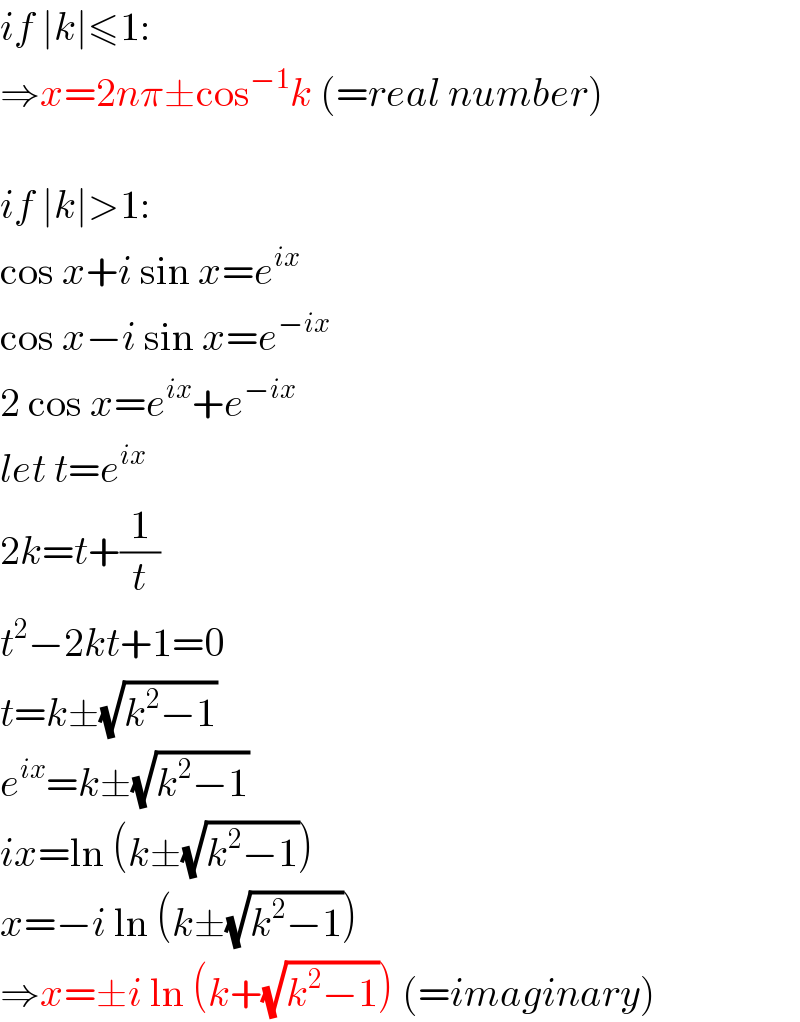
Commented by M±th+et£s last updated on 11/Apr/20
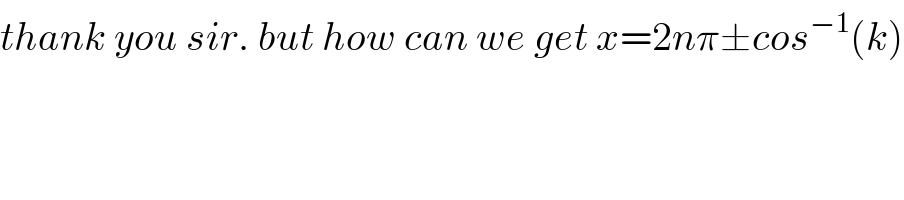
Commented by Kunal12588 last updated on 11/Apr/20
![genral solution of cos x = m ; m∈[−1,1] is x=2nπ±cos^(−1) m ; n∈Z](Q88531.png)
| ||
Question and Answers Forum | ||
Question Number 88491 by M±th+et£s last updated on 11/Apr/20 | ||
 | ||
Answered by mr W last updated on 11/Apr/20 | ||
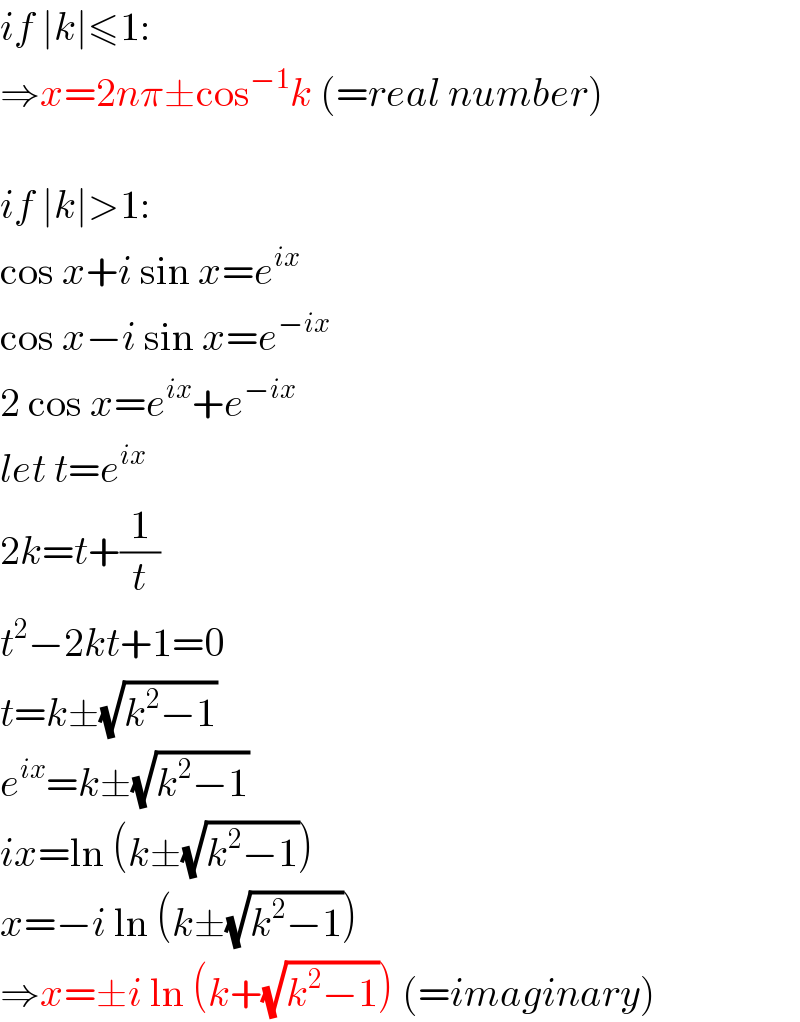 | ||
| ||
Commented by M±th+et£s last updated on 11/Apr/20 | ||
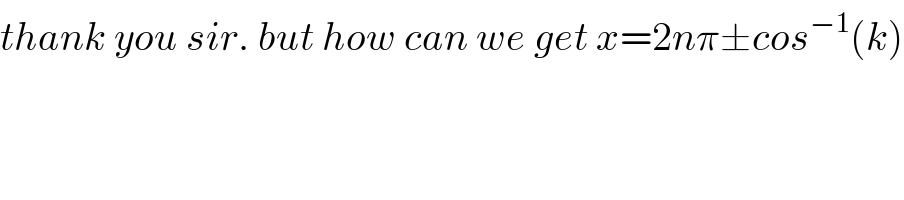 | ||
Commented by Kunal12588 last updated on 11/Apr/20 | ||
![genral solution of cos x = m ; m∈[−1,1] is x=2nπ±cos^(−1) m ; n∈Z](Q88531.png) | ||