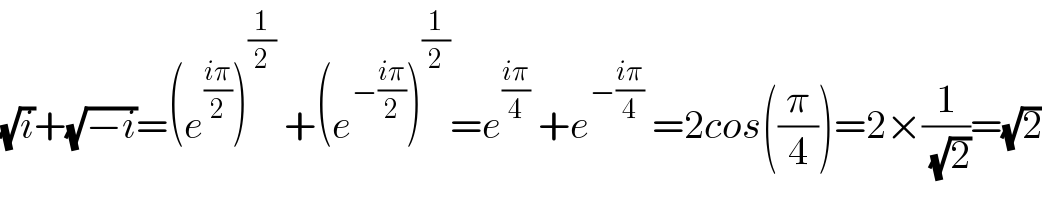Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 88678 by Cheyboy last updated on 12/Apr/20

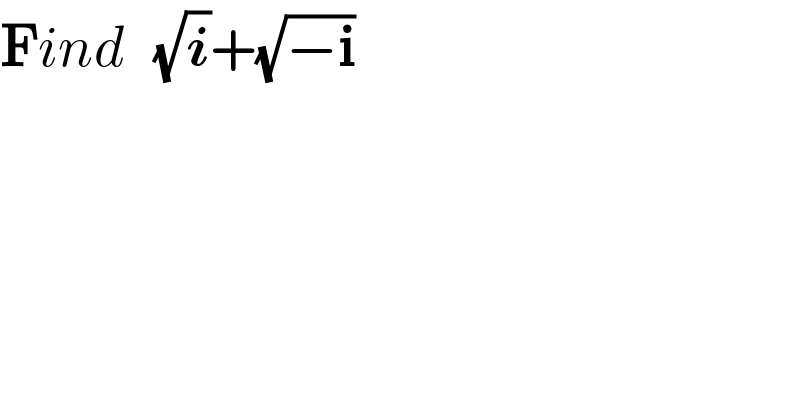
Find (√i)+(√(−i))

$$\boldsymbol{\mathrm{F}}{ind}\:\:\:\sqrt{\boldsymbol{{i}}}+\sqrt{−\boldsymbol{\mathrm{i}}} \\ $$

Commented by mr W last updated on 12/Apr/20

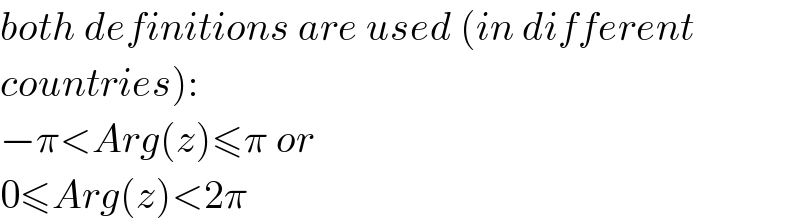
both definitions are used (in different countries): −π<Arg(z)≤π or 0≤Arg(z)<2π

$${both}\:{definitions}\:{are}\:{used}\:\left({in}\:{different}\right. \\ $$$$\left.{countries}\right): \\ $$$$−\pi<{Arg}\left({z}\right)\leqslant\pi\:{or} \\ $$$$\mathrm{0}\leqslant{Arg}\left({z}\right)<\mathrm{2}\pi \\ $$

Commented by mr W last updated on 12/Apr/20

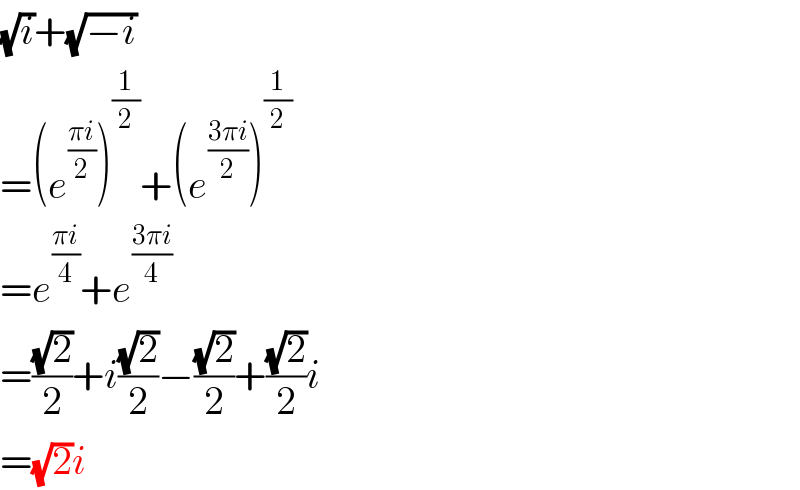
(√i)+(√(−i)) =(e^((πi)/2) )^(1/2) +(e^((3πi)/2) )^(1/2) =e^((πi)/4) +e^((3πi)/4) =((√2)/2)+i((√2)/2)−((√2)/2)+((√2)/2)i =(√2)i

$$\sqrt{{i}}+\sqrt{−{i}} \\ $$$$=\left({e}^{\frac{\pi{i}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} +\left({e}^{\frac{\mathrm{3}\pi{i}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$={e}^{\frac{\pi{i}}{\mathrm{4}}} +{e}^{\frac{\mathrm{3}\pi{i}}{\mathrm{4}}} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{i} \\ $$$$=\sqrt{\mathrm{2}}{i} \\ $$

Commented by Cheyboy last updated on 12/Apr/20

Thank your sir

$${Thank}\:{your}\:{sir} \\ $$

Commented by Tony Lin last updated on 12/Apr/20

i=cos(π/2)+isin(π/2) (√i)=cos(π/4)+isin(π/4) −i=cos(−(π/2))+isin(−(π/2)) (√(−i))=cos(−(π/4))+isin(−(π/4)) (√i)+(√(−i))=cos(π/4)+cos(−(π/4))+i[sin(π/4)+sin(−(π/4))] =(√2)

$${i}={cos}\frac{\pi}{\mathrm{2}}+{isin}\frac{\pi}{\mathrm{2}} \\ $$$$\sqrt{{i}}={cos}\frac{\pi}{\mathrm{4}}+{isin}\frac{\pi}{\mathrm{4}} \\ $$$$−{i}={cos}\left(−\frac{\pi}{\mathrm{2}}\right)+{isin}\left(−\frac{\pi}{\mathrm{2}}\right) \\ $$$$\sqrt{−{i}}={cos}\left(−\frac{\pi}{\mathrm{4}}\right)+{isin}\left(−\frac{\pi}{\mathrm{4}}\right) \\ $$$$\sqrt{{i}}+\sqrt{−{i}}={cos}\frac{\pi}{\mathrm{4}}+{cos}\left(−\frac{\pi}{\mathrm{4}}\right)+{i}\left[{sin}\frac{\pi}{\mathrm{4}}+{sin}\left(−\frac{\pi}{\mathrm{4}}\right)\right] \\ $$$$=\sqrt{\mathrm{2}} \\ $$

Commented by ajfour last updated on 12/Apr/20

−π<Arg(z)≤π is this true, sir?

$$−\pi<{Arg}\left({z}\right)\leqslant\pi \\ $$$${is}\:{this}\:{true},\:{sir}? \\ $$

Commented by mr W last updated on 12/Apr/20

Commented by ajfour last updated on 12/Apr/20

thanks Sir.

$${thanks}\:{Sir}. \\ $$

Commented by mathmax by abdo last updated on 12/Apr/20

(√i)+(√(−i))=(e^((iπ)/2) )^(1/2) +(e^(−((iπ)/2)) )^(1/2) =e^((iπ)/4) +e^(−((iπ)/4)) =2cos((π/4))=2×(1/(√2))=(√2)

$$\sqrt{{i}}+\sqrt{−{i}}=\left({e}^{\frac{{i}\pi}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\left({e}^{−\frac{{i}\pi}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} ={e}^{\frac{{i}\pi}{\mathrm{4}}} \:+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:=\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{4}}\right)=\mathrm{2}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}=\sqrt{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com