
Question and Answers Forum
Question Number 88710 by jagoll last updated on 12/Apr/20
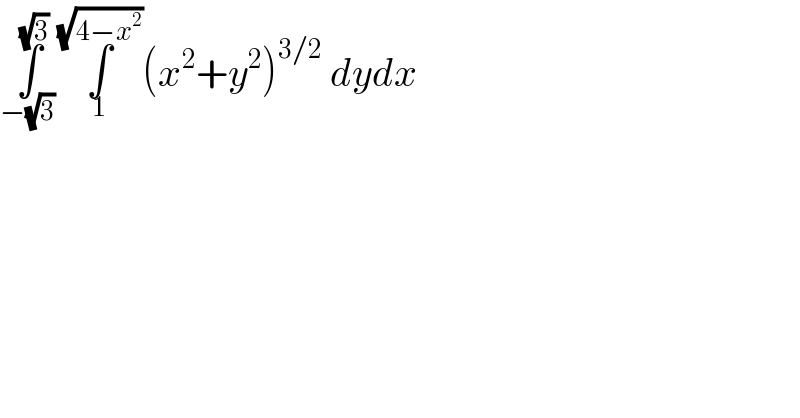
Commented by mathmax by abdo last updated on 12/Apr/20
![I =∫_(−(√3)) ^(√3) (∫_1 ^(√(4−x^2 )) (x^2 +y^2 )^(3/2) dy)dx =∫_(−(√3)) ^(√3) A(x)dx A(x) =∫_1 ^(√(4−x^2 )) (y^2 +x^2 )^(3/2) dy =_(y=∣x∣sh(t)) ∫_(argsh((1/(∣x∣)))) ^(argsh(((√(4−x^2 ))/(∣x∣)))) x^3 (ch^2 t)^(3/2) ∣x∣ch(t)dt =∫_(ln((1/(∣x∣))+(√(1+(1/x^2 ))))) ^(ln(((√(4−x^2 ))/(∣x∣))+(√(1+((4−x^2 )/x^2 ))))) x^3 ∣x∣ ch^4 t dt =x^3 ∣x∣ ∫_(α(x)) ^(β(x)) (((1+ch(2t))/2))^2 dt =(1/4)x^3 ∣x∣∫_(α(x)) ^(β(x)) (1+2ch(2t)+ch^2 (2t))dt =(1/4)x^3 ∣x∣(β(x)−α(x))+(1/4)[sh(2t)]_(α(x)) ^(β(x)) +(1/4)x^3 ∣x∣ ∫_(α(x)) ^(β(x)) (((1+ch(4t))/2))dt =(1/4)x^3 ∣x∣(β(x)−α(x))+(1/4)[((e^(2t) −e^(−2t) )/2)]_(α(x)) ^(β(x)) +(1/8)x^3 ∣x∣(β(x)−α(x)) +(1/(32))x^3 ∣x∣ [sh(4t)]_(α(x)) ^(β(x)) =(3/8)x^3 ∣x∣(β(x)−α(x))+(1/8){e^(2β(x)) −e^(−2α(x)) −e^(2α(x)) +e^(−2α(x)) } +(1/(64))x^3 ∣x∣{e^(4β(x)) −e^(−4β(x)) −e^(4α(x)) +e^(−4α(x)) }....be continued...](Q88728.png)
Answered by john santu last updated on 12/Apr/20
![let me try. to converting to polar coordinates y =(√(4−x^2 )) ⇒ { ((y=1)),((r=2 , θ = (π/6), ((5π)/6))) :} I = ∫_(π/6) ^((5π)/6) ∫_(csc θ) ^2 (r^2 )^(3/2) (r dr dθ) I = ∫_(π/6) ^((5π)/6) ∫_(csc θ) ^2 r^4 dr dθ I = ∫_(π/6) ^((5π)/6) {(1/5)r^5 ]_(csc θ) ^2 } dθ I = (1/5)∫_(π/6) ^((5π)/6) (32−csc^5 θ ) dθ I = (1/5)(((64π)/3) −∫_(π/6) ^((5π)/6) csc^5 θ dθ) I = ((64π)/(15)) −(1/5) [−(1/4) csc^3 θ cot θ − (3/8)csc θ cot θ −(3/8) ln ∣ csc θ + cot θ ∣ ]^((5π)/6) _( (π/6)) I = (1/(60)) ( 256π −9 ln (2+(√3) )−66(√3) )](Q88730.png)
Commented by jagoll last updated on 12/Apr/20

Answered by mr W last updated on 12/Apr/20
![I=∫_(−(√3) ) ^(√3) ∫_1 ^(√(4−x^2 )) (x^2 +y^2 )^(3/2) dydx =2∫_( 0 ) ^(√3) ∫_1 ^(√(4−x^2 )) (x^2 +y^2 )^(3/2) dydx =2∫_(π/6) ^(π/2) ∫_(1/(sin θ)) ^( 2) r^4 drdθ =(2/5)∫_(π/6) ^(π/2) (2^5 −(1/(sin^5 θ)))dθ =(2/5)[32((π/2)−(π/6))−∫_(π/6) ^(π/2) (dθ/(sin^5 θ))] =(2/5)[((32π)/3)−∫_(π/6) ^(π/2) (dθ/(sin^5 θ))] =(2/5)[((32π)/3)−((11(√3))/4)−((3 ln (2+(√3)))/8)] =(1/(60))[256π−66(√3)−9 ln (2+(√3))] ≈11.301 ∫_(π/6) ^(π/2) (dθ/(sin^5 θ)) =∫_(π/6) ^(π/2) ((sin θdθ)/(sin^6 θ)) =−∫_(π/6) ^(π/2) ((d(cos θ))/((1−cos^2 θ)^3 )) =∫_0 ^((√3)/2) (du/((1−u^2 )^3 )) ...... =(3/8)ln (2+(√3))+((11(√3))/4)](Q88736.png)
Commented by mr W last updated on 12/Apr/20
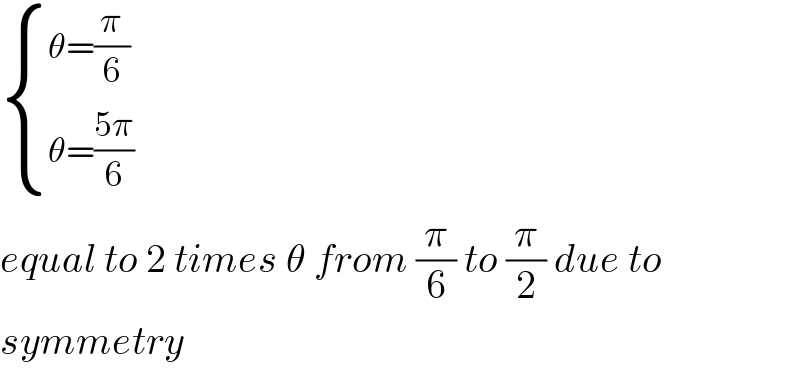
Commented by john santu last updated on 12/Apr/20
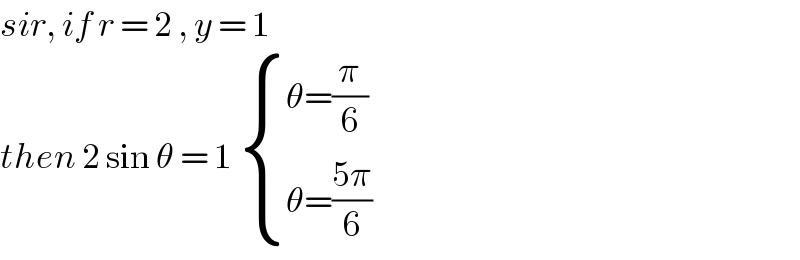
Commented by mr W last updated on 12/Apr/20
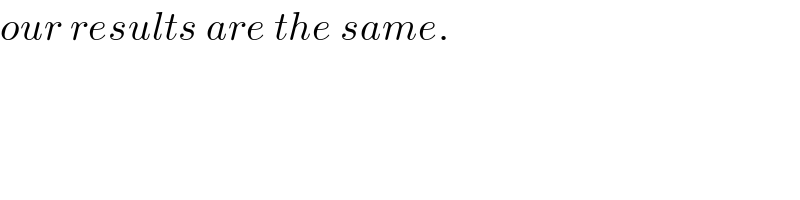
Commented by john santu last updated on 12/Apr/20
Commented by jagoll last updated on 12/Apr/20

