
Question Number 88754 by ajfour last updated on 12/Apr/20

Commented by mr W last updated on 13/Apr/20

$${there}\:{is}\:{no}\:{unique}\:{solution}\:{for}\:\frac{{b}}{{a}}. \\ $$$${we}\:{can}\:{only}\:{find}\:{the}\:{correlation}\:{between} \\ $$$${a}\:{and}\:{b}. \\ $$
Commented by mr W last updated on 13/Apr/20

Commented by mr W last updated on 13/Apr/20

$${b}_{{max}} \:{is}\:{when}\:{a}=\mathrm{0} \\ $$$${b}_{{min}} {is}\:\mathrm{0}\:{when}\:{a}_{{max}} \:\left({red}\:{marked}\right) \\ $$$${between}\:{both}\:{extrem}\:{cases}\:{there}\:{are} \\ $$$${infinite}\:{possibilities}. \\ $$
Answered by mr W last updated on 13/Apr/20

Commented by mr W last updated on 13/Apr/20
![say radius of big quarter circle is R. tan α=(a/(R−a)) OE=R tan (2α)=R×((2×(a/(R−a)))/(1−((a/(R−a)))^2 ))=((2(R−a)a)/(R−2a)) tan β=(a/(((2(R−a)a)/(R−2a))−a))=((R−2a)/R) tan γ=(a/((√((R−a)^2 −a^2 ))−((2(R−a)a)/(R−2a))))=(((R−2a)a)/((R−2a)(√(R(R−2a)))−2(R−a)a)) β+δ+γ=(π/2) ⇒δ=(π/2)−β−γ ∠OEB=2β+δ=(π/2)+β−γ OB=R−b OB^2 =OE^2 +EB^2 −2×OE×cos ∠OEB×EB EB^2 −2×OE×cos ∠OEB×EB+OE^2 −OB^2 =0 EB^2 −((4(R−a)a)/(R−2a))×sin (γ−β)×EB+[((2(R−a)a)/(R−2a))]^2 −(R−b)^2 =0 EB=(b/(sin δ))=(b/(cos (β+γ))) [(b/(cos (β+γ)))]^2 −((4(R−a)a)/(R−2a))×sin (γ−β)×(b/(cos (β+γ)))+[((2(R−a)a)/(R−2a))]^2 −(R−b)^2 =0 let μ=(a/R), ν=(b/R) ⇒β=tan^(−1) (1−2μ) ⇒γ=tan^(−1) (((1−2μ)μ)/((1−2μ)^(3/2) −2(1−μ)μ)) (ν^2 /(cos^2 (β+γ)))−((4(1−μ)μν)/(1−2μ))×((sin (γ−β))/(cos (β+γ)))+[((2(1−μ)μ)/(1−2μ))]^2 −(1−ν)^2 =0 let λ=(b/a)=(ν/μ) ((μ^2 λ^2 )/(cos^2 (β+γ)))−((4(1−μ)μ^2 λ)/(1−2μ))×((sin (γ−β))/(cos (β+γ)))+[((2(1−μ)μ)/(1−2μ))]^2 −(1−μλ)^2 =0 tan^2 (α+γ)λ^2 −2[((2(1−μ))/(1−2μ))×((sin (γ−β))/(cos (β+γ)))−(1/μ)]λ−[(1/μ^2 )−((4(1−μ)^2 )/((1−2μ)^2 ))]=0 ⇒λ=(1/(tan^2 (β+γ))){((2(1−μ) sin (γ−β))/((1−2μ) cos (β+γ)))−(1/μ)+(√([((2(1−μ) sin (γ−β))/((1−2μ) cos (β+γ)))−(1/μ)]^2 +tan^2 (α+γ)[(1/μ^2 )−((4(1−μ)^2 )/((1−2μ)^2 ))]))} we see λ is not a constant, but a function of μ, since there are infinite circles with radii a and b. a_(max) is when b=0, δ=0, i.e. β+γ=(π/2) tan γ=(1/(tan β)) (((1−2μ)μ)/((1−2μ)^(3/2) −2(1−μ)μ))=(1/(1−2μ)) (1−2μ)^(3/2) −2(1−μ)μ=μ(1−2μ)^2 μ=0.2222 i.e. a≤0.2222R (√2)b_(max) =R−b_(max) ⇒b_(max) =(R/(1+(√2)))≈0.4142R](Q88823.png)
$${say}\:{radius}\:{of}\:{big}\:{quarter}\:{circle}\:{is}\:{R}. \\ $$$$\mathrm{tan}\:\alpha=\frac{{a}}{{R}−{a}} \\ $$$${OE}={R}\:\mathrm{tan}\:\left(\mathrm{2}\alpha\right)={R}×\frac{\mathrm{2}×\frac{{a}}{{R}−{a}}}{\mathrm{1}−\left(\frac{{a}}{{R}−{a}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}\left({R}−{a}\right){a}}{{R}−\mathrm{2}{a}} \\ $$$$\mathrm{tan}\:\beta=\frac{{a}}{\frac{\mathrm{2}\left({R}−{a}\right){a}}{{R}−\mathrm{2}{a}}−{a}}=\frac{{R}−\mathrm{2}{a}}{{R}} \\ $$$$\mathrm{tan}\:\gamma=\frac{{a}}{\sqrt{\left({R}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }−\frac{\mathrm{2}\left({R}−{a}\right){a}}{{R}−\mathrm{2}{a}}}=\frac{\left({R}−\mathrm{2}{a}\right){a}}{\left({R}−\mathrm{2}{a}\right)\sqrt{{R}\left({R}−\mathrm{2}{a}\right)}−\mathrm{2}\left({R}−{a}\right){a}} \\ $$$$\beta+\delta+\gamma=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\delta=\frac{\pi}{\mathrm{2}}−\beta−\gamma \\ $$$$\angle{OEB}=\mathrm{2}\beta+\delta=\frac{\pi}{\mathrm{2}}+\beta−\gamma \\ $$$${OB}={R}−{b} \\ $$$${OB}^{\mathrm{2}} ={OE}^{\mathrm{2}} +{EB}^{\mathrm{2}} −\mathrm{2}×{OE}×\mathrm{cos}\:\angle{OEB}×{EB} \\ $$$${EB}^{\mathrm{2}} −\mathrm{2}×{OE}×\mathrm{cos}\:\angle{OEB}×{EB}+{OE}^{\mathrm{2}} −{OB}^{\mathrm{2}} =\mathrm{0} \\ $$$${EB}^{\mathrm{2}} −\frac{\mathrm{4}\left({R}−{a}\right){a}}{{R}−\mathrm{2}{a}}×\mathrm{sin}\:\left(\gamma−\beta\right)×{EB}+\left[\frac{\mathrm{2}\left({R}−{a}\right){a}}{{R}−\mathrm{2}{a}}\right]^{\mathrm{2}} −\left({R}−{b}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${EB}=\frac{{b}}{\mathrm{sin}\:\delta}=\frac{{b}}{\mathrm{cos}\:\left(\beta+\gamma\right)} \\ $$$$\left[\frac{{b}}{\mathrm{cos}\:\left(\beta+\gamma\right)}\right]^{\mathrm{2}} −\frac{\mathrm{4}\left({R}−{a}\right){a}}{{R}−\mathrm{2}{a}}×\mathrm{sin}\:\left(\gamma−\beta\right)×\frac{{b}}{\mathrm{cos}\:\left(\beta+\gamma\right)}+\left[\frac{\mathrm{2}\left({R}−{a}\right){a}}{{R}−\mathrm{2}{a}}\right]^{\mathrm{2}} −\left({R}−{b}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:\mu=\frac{{a}}{{R}},\:\nu=\frac{{b}}{{R}} \\ $$$$\Rightarrow\beta=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{2}\mu\right) \\ $$$$\Rightarrow\gamma=\mathrm{tan}^{−\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{2}\mu\right)\mu}{\left(\mathrm{1}−\mathrm{2}\mu\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{2}\left(\mathrm{1}−\mu\right)\mu} \\ $$$$\frac{\nu^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:\left(\beta+\gamma\right)}−\frac{\mathrm{4}\left(\mathrm{1}−\mu\right)\mu\nu}{\mathrm{1}−\mathrm{2}\mu}×\frac{\mathrm{sin}\:\left(\gamma−\beta\right)}{\mathrm{cos}\:\left(\beta+\gamma\right)}+\left[\frac{\mathrm{2}\left(\mathrm{1}−\mu\right)\mu}{\mathrm{1}−\mathrm{2}\mu}\right]^{\mathrm{2}} −\left(\mathrm{1}−\nu\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:\lambda=\frac{{b}}{{a}}=\frac{\nu}{\mu} \\ $$$$\frac{\mu^{\mathrm{2}} \lambda^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:\left(\beta+\gamma\right)}−\frac{\mathrm{4}\left(\mathrm{1}−\mu\right)\mu^{\mathrm{2}} \lambda}{\mathrm{1}−\mathrm{2}\mu}×\frac{\mathrm{sin}\:\left(\gamma−\beta\right)}{\mathrm{cos}\:\left(\beta+\gamma\right)}+\left[\frac{\mathrm{2}\left(\mathrm{1}−\mu\right)\mu}{\mathrm{1}−\mathrm{2}\mu}\right]^{\mathrm{2}} −\left(\mathrm{1}−\mu\lambda\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\left(\alpha+\gamma\right)\lambda^{\mathrm{2}} −\mathrm{2}\left[\frac{\mathrm{2}\left(\mathrm{1}−\mu\right)}{\mathrm{1}−\mathrm{2}\mu}×\frac{\mathrm{sin}\:\left(\gamma−\beta\right)}{\mathrm{cos}\:\left(\beta+\gamma\right)}−\frac{\mathrm{1}}{\mu}\right]\lambda−\left[\frac{\mathrm{1}}{\mu^{\mathrm{2}} }−\frac{\mathrm{4}\left(\mathrm{1}−\mu\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{2}\mu\right)^{\mathrm{2}} }\right]=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\left(\beta+\gamma\right)}\left\{\frac{\mathrm{2}\left(\mathrm{1}−\mu\right)\:\mathrm{sin}\:\left(\gamma−\beta\right)}{\left(\mathrm{1}−\mathrm{2}\mu\right)\:\mathrm{cos}\:\left(\beta+\gamma\right)}−\frac{\mathrm{1}}{\mu}+\sqrt{\left[\frac{\mathrm{2}\left(\mathrm{1}−\mu\right)\:\mathrm{sin}\:\left(\gamma−\beta\right)}{\left(\mathrm{1}−\mathrm{2}\mu\right)\:\mathrm{cos}\:\left(\beta+\gamma\right)}−\frac{\mathrm{1}}{\mu}\right]^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\left(\alpha+\gamma\right)\left[\frac{\mathrm{1}}{\mu^{\mathrm{2}} }−\frac{\mathrm{4}\left(\mathrm{1}−\mu\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{2}\mu\right)^{\mathrm{2}} }\right]}\right\} \\ $$$${we}\:{see}\:\lambda\:{is}\:{not}\:{a}\:{constant},\:{but}\:{a}\:{function}\:{of}\:\mu, \\ $$$${since}\:{there}\:{are}\:{infinite}\:{circles}\:{with} \\ $$$${radii}\:{a}\:{and}\:{b}. \\ $$$$ \\ $$$${a}_{{max}} \:{is}\:{when}\:{b}=\mathrm{0},\:\delta=\mathrm{0},\:{i}.{e}.\:\beta+\gamma=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\gamma=\frac{\mathrm{1}}{\mathrm{tan}\:\beta} \\ $$$$\frac{\left(\mathrm{1}−\mathrm{2}\mu\right)\mu}{\left(\mathrm{1}−\mathrm{2}\mu\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{2}\left(\mathrm{1}−\mu\right)\mu}=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2}\mu} \\ $$$$\left(\mathrm{1}−\mathrm{2}\mu\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{2}\left(\mathrm{1}−\mu\right)\mu=\mu\left(\mathrm{1}−\mathrm{2}\mu\right)^{\mathrm{2}} \\ $$$$\mu=\mathrm{0}.\mathrm{2222} \\ $$$${i}.{e}.\:{a}\leqslant\mathrm{0}.\mathrm{2222}{R} \\ $$$$ \\ $$$$\sqrt{\mathrm{2}}{b}_{{max}} ={R}−{b}_{{max}} \\ $$$$\Rightarrow{b}_{{max}} =\frac{{R}}{\mathrm{1}+\sqrt{\mathrm{2}}}\approx\mathrm{0}.\mathrm{4142}{R} \\ $$
Commented by ajfour last updated on 13/Apr/20

$${Sir},\:{sorry}\:{for}\:{my}\:{poor}\:{under}- \\ $$$${standing}\:{earlier},\:{I}\:{understand}, \\ $$$${totally}\:{agree},\:{and}\:{am}\:{extremely} \\ $$$${thankful}\:{to}\:{you}\:{for}\:{explanaton}. \\ $$$$ \\ $$
Commented by mr W last updated on 13/Apr/20

Commented by mr W last updated on 13/Apr/20

Commented by ajfour last updated on 13/Apr/20
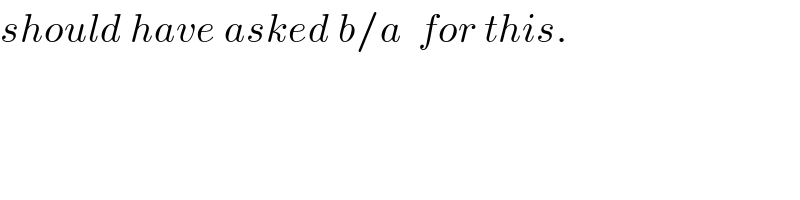
$${should}\:{have}\:{asked}\:{b}/{a}\:\:{for}\:{this}. \\ $$
Commented by ajfour last updated on 13/Apr/20

Commented by mr W last updated on 13/Apr/20
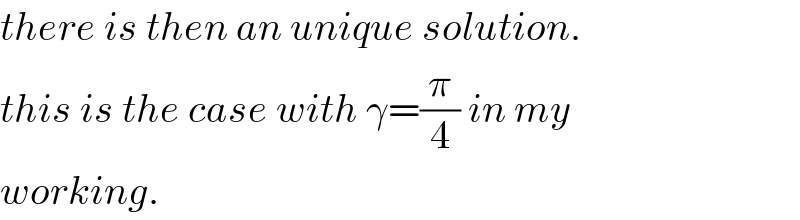
$${there}\:{is}\:{then}\:{an}\:{unique}\:{solution}. \\ $$$${this}\:{is}\:{the}\:{case}\:{with}\:\gamma=\frac{\pi}{\mathrm{4}}\:{in}\:{my} \\ $$$${working}. \\ $$
