
Question and Answers Forum
Question Number 88758 by mr W last updated on 12/Apr/20

Commented by mr W last updated on 12/Apr/20

Commented by mr W last updated on 12/Apr/20

Commented by TawaTawa1 last updated on 12/Apr/20

Commented by Learner-123 last updated on 12/Apr/20
Wonderful!
Commented by Prithwish Sen 1 last updated on 13/Apr/20

Commented by Prithwish Sen 1 last updated on 13/Apr/20

Commented by mr W last updated on 13/Apr/20

Commented by Prithwish Sen 1 last updated on 13/Apr/20

Commented by otchereabdullai@gmail.com last updated on 13/Apr/20

Commented by mr W last updated on 13/Apr/20
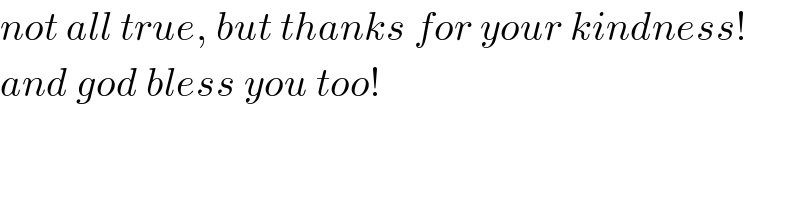
Commented by mr W last updated on 13/Apr/20
شكرا
Commented by otchereabdullai@gmail.com last updated on 13/Apr/20

Commented by I want to learn more last updated on 17/Apr/20

Commented by mr W last updated on 17/Apr/20

Commented by I want to learn more last updated on 17/Apr/20
Commented by mr W last updated on 17/Apr/20

Commented by I want to learn more last updated on 17/Apr/20

Commented by mr W last updated on 19/Apr/20

Commented by mr W last updated on 19/Apr/20

Commented by mr W last updated on 19/Apr/20

Commented by mr W last updated on 06/May/20

Commented by mr W last updated on 06/May/20
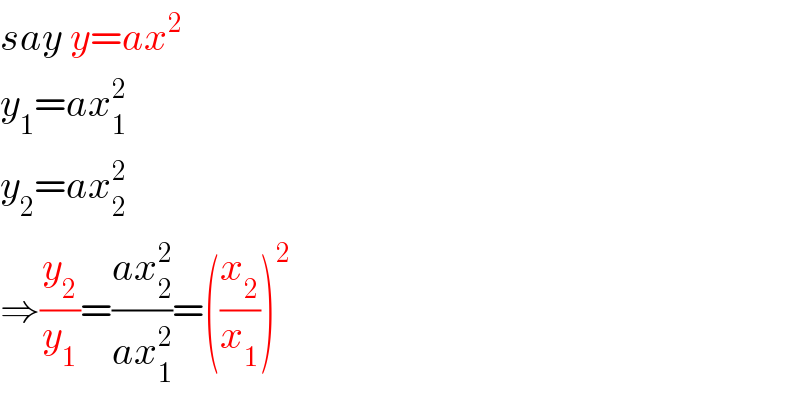
Answered by mr W last updated on 12/Apr/20

Commented by mr W last updated on 12/Apr/20

Commented by mr W last updated on 12/Apr/20
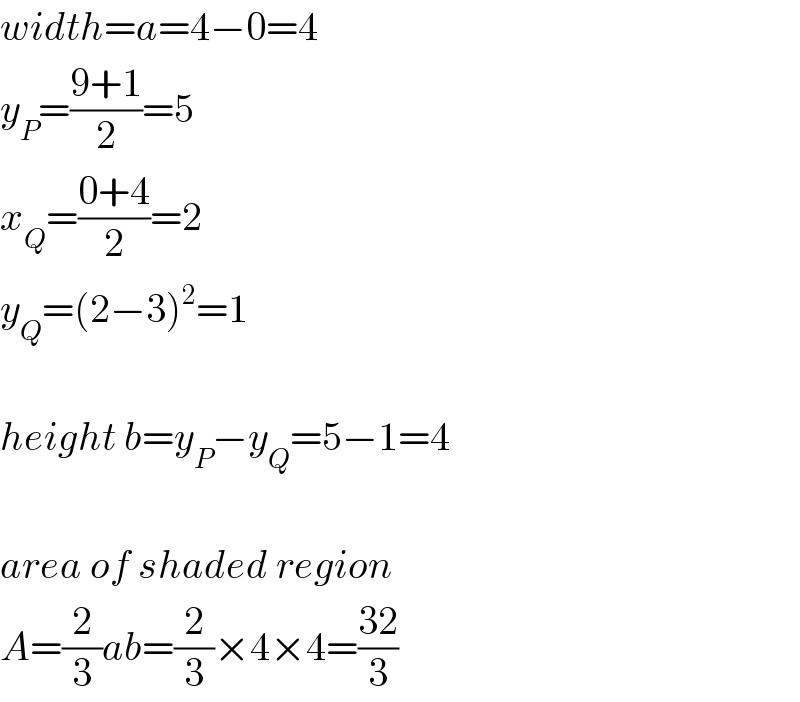
Answered by mr W last updated on 12/Apr/20

Commented by mr W last updated on 12/Apr/20

Commented by mr W last updated on 12/Apr/20

