Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 88789 by M±th+et£s last updated on 12/Apr/20

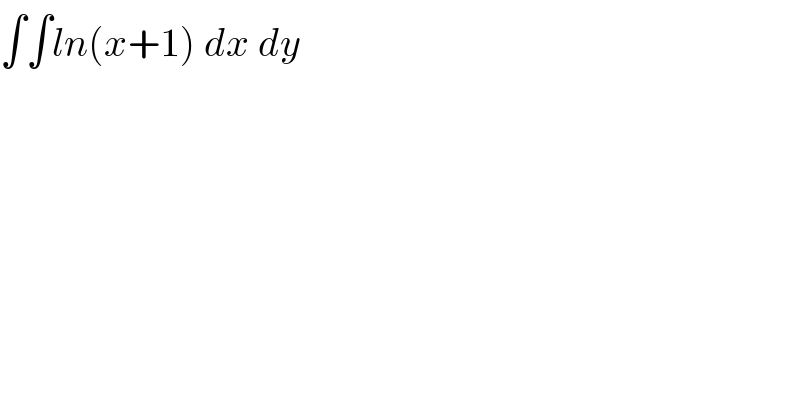
∫∫ln(x+1) dx dy

$$\int\int{ln}\left({x}+\mathrm{1}\right)\:{dx}\:{dy} \\ $$

Commented by mr W last updated on 13/Apr/20

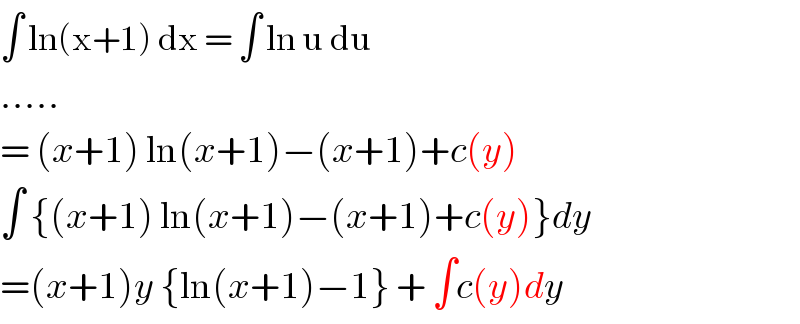
∫ ln(x+1) dx = ∫ ln u du ..... = (x+1) ln(x+1)−(x+1)+c(y) ∫ {(x+1) ln(x+1)−(x+1)+c(y)}dy =(x+1)y {ln(x+1)−1} + ∫c(y)dy

$$\int\:\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)\:\mathrm{dx}\:=\:\int\:\mathrm{ln}\:\mathrm{u}\:\mathrm{du} \\ $$$$..... \\ $$$$=\:\left({x}+\mathrm{1}\right)\:\mathrm{ln}\left({x}+\mathrm{1}\right)−\left({x}+\mathrm{1}\right)+{c}\left({y}\right) \\ $$$$\int\:\left\{\left({x}+\mathrm{1}\right)\:\mathrm{ln}\left({x}+\mathrm{1}\right)−\left({x}+\mathrm{1}\right)+{c}\left({y}\right)\right\}{dy} \\ $$$$=\left({x}+\mathrm{1}\right){y}\:\left\{\mathrm{ln}\left({x}+\mathrm{1}\right)−\mathrm{1}\right\}\:+\:\int{c}\left({y}\right){dy} \\ $$

Commented by john santu last updated on 12/Apr/20

∫ ln(x+1) dx = ∫ ln u du [ u = x+1 ] = u ln u −∫ (1/u) .udu = u ln u −u + c = (x+1) ln(x+1)−(x+1)+c ∫ {(x+1) ln(x+1)−(x+1)+c}dy =(x+1)y {ln(x+1)−1} + cy

$$\int\:\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)\:\mathrm{dx}\:=\:\int\:\mathrm{ln}\:\mathrm{u}\:\mathrm{du} \\ $$$$\left[\:\mathrm{u}\:=\:\mathrm{x}+\mathrm{1}\:\right] \\ $$$$=\:\mathrm{u}\:\mathrm{ln}\:\mathrm{u}\:−\int\:\frac{\mathrm{1}}{{u}}\:.{udu} \\ $$$$=\:{u}\:\mathrm{ln}\:{u}\:−{u}\:+\:{c} \\ $$$$=\:\left({x}+\mathrm{1}\right)\:\mathrm{ln}\left({x}+\mathrm{1}\right)−\left({x}+\mathrm{1}\right)+{c} \\ $$$$\int\:\left\{\left({x}+\mathrm{1}\right)\:\mathrm{ln}\left({x}+\mathrm{1}\right)−\left({x}+\mathrm{1}\right)+{c}\right\}{dy} \\ $$$$=\left({x}+\mathrm{1}\right){y}\:\left\{\mathrm{ln}\left({x}+\mathrm{1}\right)−\mathrm{1}\right\}\:+\:{cy} \\ $$

Commented by M±th+et£s last updated on 12/Apr/20

y?

$${y}? \\ $$

Commented by jagoll last updated on 13/Apr/20

sir. the answer mr john correct?

$${sir}.\:{the}\:{answer}\:{mr}\:{john}\:{correct}? \\ $$

Commented by mr W last updated on 13/Apr/20

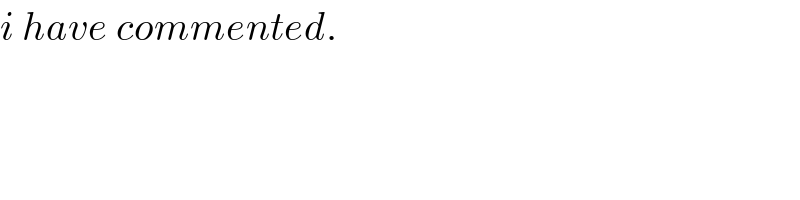
i have commented.

$${i}\:{have}\:{commented}. \\ $$

Commented by ajfour last updated on 13/Apr/20

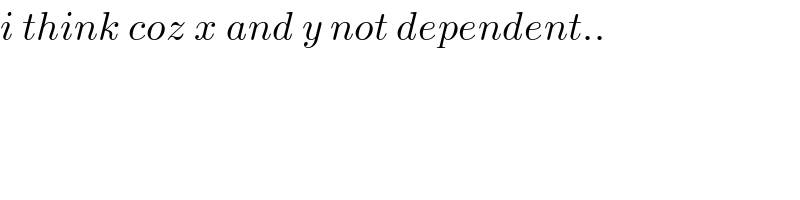
i think coz x and y not dependent..

$${i}\:{think}\:{coz}\:{x}\:{and}\:{y}\:{not}\:{dependent}.. \\ $$

Commented by jagoll last updated on 13/Apr/20

y_1 ,y_2 ,y_3 ,....?

$${y}_{\mathrm{1}} ,{y}_{\mathrm{2}} ,{y}_{\mathrm{3}} ,....? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com