
Question and Answers Forum
Question Number 88852 by M±th+et£s last updated on 13/Apr/20
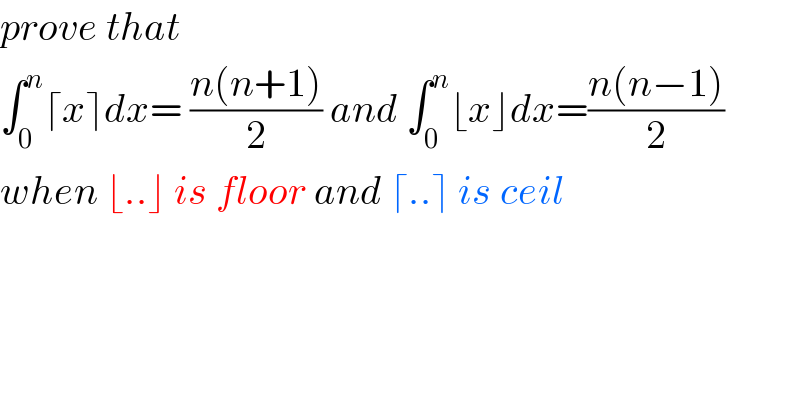
Answered by mr W last updated on 13/Apr/20
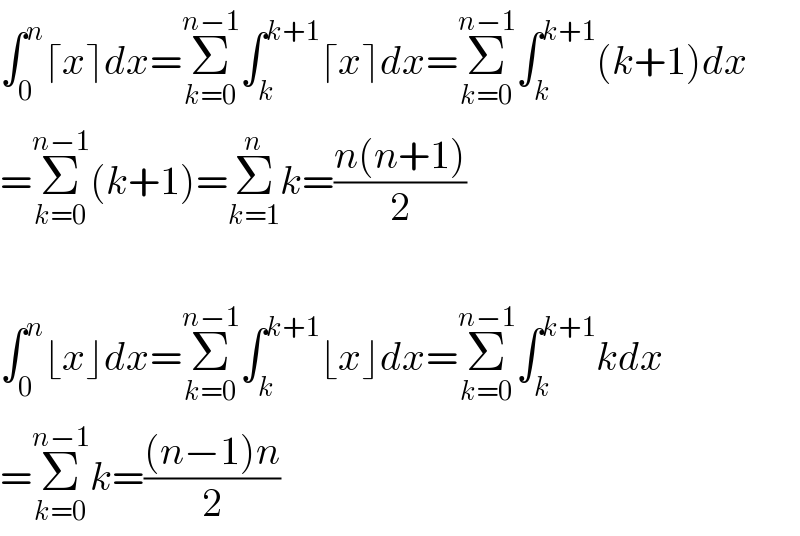
Commented by M±th+et£s last updated on 13/Apr/20

| ||
Question and Answers Forum | ||
Question Number 88852 by M±th+et£s last updated on 13/Apr/20 | ||
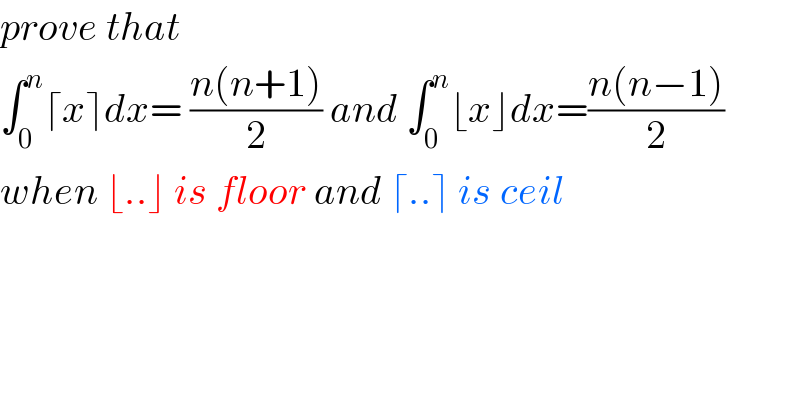 | ||
Answered by mr W last updated on 13/Apr/20 | ||
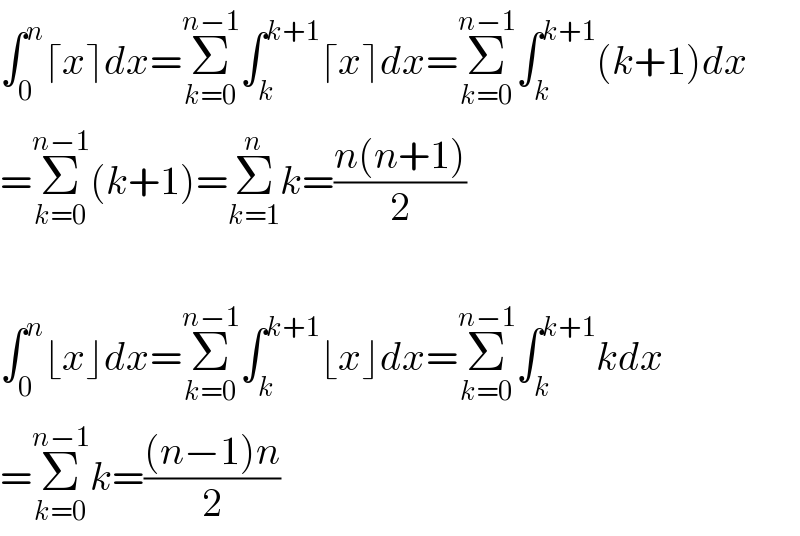 | ||
| ||
Commented by M±th+et£s last updated on 13/Apr/20 | ||
 | ||