∫_0 ^(π/2) (x/(tan(x)))dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 89052 by M±th+et£s last updated on 15/Apr/20

$\int_{0}^{\frac{π}{2}} \frac{x}{t a n (x)} d x$
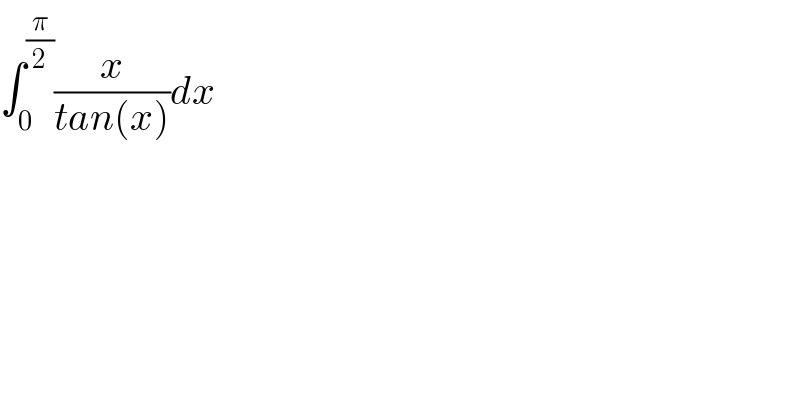
Commented by abdomathmax last updated on 15/Apr/20
$I =∫_0 ^(π/2) (x/(tanx))dx ⇒I =_(tanx=t) ∫_0 ^∞ ((arctan(t))/t)(dt/(1+t^2 )) =∫_0 ^∞ ((arctan(t))/(t(1+t^2 )))dt let f(a) =∫_0 ^∞ ((arctan(at))/(t(1+t^2 )))dt f^′ (a) =∫_0 ^∞ (dt/((1+a^2 t^2 )(1+t^2 ))) =_(at=u) ∫_0 ^∞ (du/(a(1+u^2 )(1+(u^2 /a^2 ))))(du/a) =∫_0 ^∞ (du/((1+u^2 )(a^2 +u^2 ))) decomposition of F(u) =(1/((u^2 +1)(u^2 +a^2 ))) =((αu +β)/(u^2 +1)) +((λu +ρ)/(u^2 +a^2 )) F(−u)=F(u) ⇒ ((−αu +β)/(u^2 +1)) +((−λu +ρ)/(u^2 +a^2 )) =F(u) ⇒α=λ=0 and ρ=β ⇒ F(u)=(β/(u^2 +1)) +(ρ/(u^2 +a^2 )) lim_(u→+∞) u^2 F(u) =0 =β+ρ ⇒ρ=−β ⇒ F(u)=(β/(u^2 +1))−(β/(u^2 +a^2 )) F(0)=(1/a^2 ) =β−(β/a^2 ) ⇒1 =a^2 β−β =(a^2 −1)β ⇒ β =(1/(a^2 −1)) ⇒F(u)=(1/(a^2 −1))((1/(u^2 +1))−(1/(u^2 +a^2 ))) ⇒ f^′ (a)=(1/(a^2 −1))∫_0 ^∞ ((1/(u^2 +1))−(1/(u^2 +a^2 )))du ∫ (du/(u^2 +a^2 )) =_(u=az) ∫ ((adz)/(a^2 (1+z^2 ))) =(1/a) arctan((u/a)) ⇒ f^′ (a) =(1/(a^2 −1))[arctanu −(1/a)arctan((u/a))]_0 ^(+∞) =(1/(a^2 −1)){(π/2)−(π/(2a))} =(π/2)×(1/(a^2 −1))(1−(1/a)) =(π/(2(a^2 −1)))(((a−1)/a)) =(π/(2a(a+1))) ⇒ f(a) =(π/2) ∫ (da/(a(a+1))) +c =(π/2)∫((1/a)−(1/(a+1)))da +c =(π/2)ln∣(a/(a+1))∣ +c c =lim_(a→+∞) f(a) I =f(1) =(π/2)ln((1/2)) +c =c−(π/2)ln(2) rest to find c...$
$I = \int_{0}^{\frac{π}{2}} \frac{x}{t a n x} d x \Rightarrow I =_{t a n x = t} \int_{0}^{\infty} \frac{a r c t a n (t)}{t} \frac{d t}{1 + t^{2}}$ $= \int_{0}^{\infty} \frac{a r c t a n (t)}{t (1 + t^{2})} d t l e t f (a) = \int_{0}^{\infty} \frac{a r c t a n (a t)}{t (1 + t^{2})} d t$ $f^{^{'}} (a) = \int_{0}^{\infty} \frac{d t}{(1 + a^{2} t^{2}) (1 + t^{2})}$ $=_{a t = u} \int_{0}^{\infty} \frac{d u}{a (1 + u^{2}) (1 + \frac{u^{2}}{a^{2}})} \frac{d u}{a}$ $= \int_{0}^{\infty} \frac{d u}{(1 + u^{2}) (a^{2} + u^{2})} d e c o m p o s i t i o n o f$ $F (u) = \frac{1}{(u^{2} + 1) (u^{2} + a^{2})} = \frac{α u + β}{u^{2} + 1} + \frac{λ u + ρ}{u^{2} + a^{2}}$ $F (- u) = F (u) \Rightarrow$ $\frac{- α u + β}{u^{2} + 1} + \frac{- λ u + ρ}{u^{2} + a^{2}} = F (u) \Rightarrow α = λ = 0 a n d ρ = β \Rightarrow$ $F (u) = \frac{β}{u^{2} + 1} + \frac{ρ}{u^{2} + a^{2}}$ ${l i m}_{u \to + \infty} u^{2} F (u) = 0 = β + ρ \Rightarrow ρ = - β \Rightarrow$ $F (u) = \frac{β}{u^{2} + 1} - \frac{β}{u^{2} + a^{2}}$ $F (0) = \frac{1}{a^{2}} = β - \frac{β}{a^{2}} \Rightarrow 1 = a^{2} β - β = (a^{2} - 1) β \Rightarrow$ $β = \frac{1}{a^{2} - 1} \Rightarrow F (u) = \frac{1}{a^{2} - 1} (\frac{1}{u^{2} + 1} - \frac{1}{u^{2} + a^{2}}) \Rightarrow$ $f^{^{'}} (a) = \frac{1}{a^{2} - 1} \int_{0}^{\infty} (\frac{1}{u^{2} + 1} - \frac{1}{u^{2} + a^{2}}) d u$ $\int \frac{d u}{u^{2} + a^{2}} =_{u = a z} \int \frac{a d z}{a^{2} (1 + z^{2})} = \frac{1}{a} a r c t a n (\frac{u}{a}) \Rightarrow$ $f^{^{'}} (a) = \frac{1}{a^{2} - 1} {[a r c t a n u - \frac{1}{a} a r c t a n (\frac{u}{a})]}_{0}^{+ \infty}$ $= \frac{1}{a^{2} - 1} {\frac{π}{2} - \frac{π}{2 a}} = \frac{π}{2} \times \frac{1}{a^{2} - 1} (1 - \frac{1}{a})$ $= \frac{π}{2 (a^{2} - 1)} (\frac{a - 1}{a}) = \frac{π}{2 a (a + 1)} \Rightarrow$ $f (a) = \frac{π}{2} \int \frac{d a}{a (a + 1)} + c$ $= \frac{π}{2} \int (\frac{1}{a} - \frac{1}{a + 1}) d a + c = \frac{π}{2} l n ∣ \frac{a}{a + 1} ∣ + c$ $c = {l i m}_{a \to + \infty} f (a)$ $I = f (1) = \frac{π}{2} l n (\frac{1}{2}) + c = c - \frac{π}{2} l n (2)$ $r e s t t o f i n d c . . .$
Commented by abdomathmax last updated on 15/Apr/20
$let try residus method we?hsve I?=∫_0 ^∞ ((arctan(t))/(t(1+t^2 )))dx⇒2I =∫_(−∞) ^(+∞) ((arctan(t))/(t(1+t^2 )))dt let ϕ(z)=((arctan(z))/(z(1+z^2 ))) ⇒ϕ(z) =((arctanz)/(z(z−i)(z+i))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ {Res(ϕ,i) +Res(ϕ,o)} =2iπ×((arctan(i))/(i(2i))) =−iπ arctan(i) but the frmula arctan(z)=(1/(2i))ln(((1+iz)/(1−iz))) is not valide for z=i...be continued...$
$l e t t r y r e s i d u s m e t h o d w e ? h s v e$ $I ? = \int_{0}^{\infty} \frac{a r c t a n (t)}{t (1 + t^{2})} d x \Rightarrow 2 I = \int_{- \infty}^{+ \infty} \frac{a r c t a n (t)}{t (1 + t^{2})} d t$ $l e t φ (z) = \frac{a r c t a n (z)}{z (1 + z^{2})} \Rightarrow φ (z) = \frac{a r c t a n z}{z (z - i) (z + i)}$ $\int_{- \infty}^{+ \infty} φ (z) d z = 2 i π {R e s (φ, i) + R e s (φ, o)}$ $= 2 i π \times \frac{a r c t a n (i)}{i (2 i)} = - i π a r c t a n (i)$ $b u t t h e f r m u l a a r c t a n (z) = \frac{1}{2 i} l n (\frac{1 + i z}{1 - i z}) i s n o t$ $v a l i d e f o r z = i . . . b e c o n t i n u e d . . .$
Commented by M±th+et£s last updated on 15/Apr/20

$t h a n x s i r$
Commented by mathmax by abdo last updated on 15/Apr/20

$y o u a r e w e l c o m e$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum