Math Question and Answers


Question and Answers Forum

All Questions Topic List
Coordinate Geometry Questions
Previous in All Question Next in All Question
Previous in Coordinate Geometry Next in Coordinate Geometry
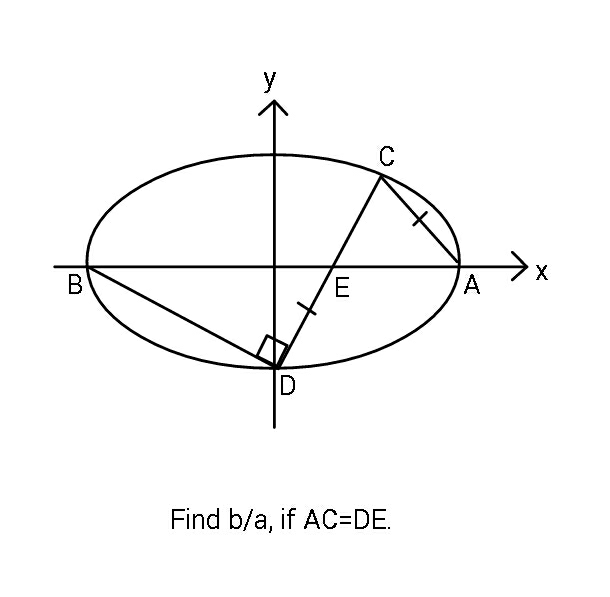
Question Number 89192 by ajfour last updated on 16/Apr/20

Commented by Prithwish Sen 1 last updated on 16/Apr/20

$Is E the focus ?$
Commented by ajfour last updated on 16/Apr/20

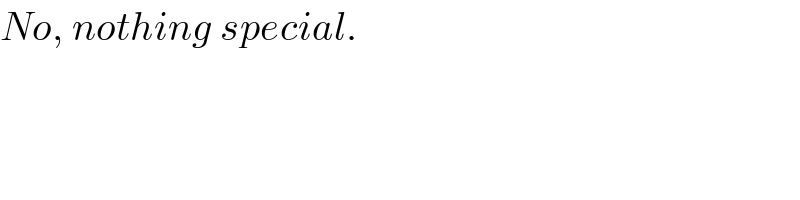
$N o, n o t h i n g s p e c i a l .$
	Answered by mr W last updated on 16/Apr/20

	$l e t μ = \frac{b}{a}$ $s a y C (a \cos θ, b \sin θ)$ $s a y C A = D E = s$ $s^{2} = {(1 - \cos θ)}^{2} a^{2} + \sin^{2} θ b^{2}$ $\frac{a \cos θ}{b (1 + \sin θ)} = \frac{b}{a}$ $\Rightarrow \frac{\cos θ}{1 + \sin θ} = μ^{2}$ $l e t t = \tan \frac{θ}{2}$ $\frac{\frac{1 - t^{2}}{1 + t^{2}}}{1 + \frac{2 t}{1 + t^{2}}} = μ^{2}$ $\Rightarrow \frac{1 - t}{1 + t} = μ^{2}$ $\Rightarrow t = \frac{1 - μ^{2}}{1 + μ^{2}}$ $D E = \frac{b}{b (1 + \sin θ)} \times D C$ $s^{2} = \frac{1}{{(1 + \sin θ)}^{2}} \times {D C}^{2} = \frac{b^{2} {(1 + \sin θ)}^{2} + a^{2} \cos^{2} θ}{{(1 + \sin θ)}^{2}}$ $s^{2} = b^{2} + \frac{a^{2} \cos^{2} θ}{{(1 + \sin θ)}^{2}} = b^{2} + (\frac{1 - \sin θ}{1 + \sin θ}) a^{2}$ $b^{2} + (\frac{1 - \sin θ}{1 + \sin θ}) a^{2} = {(1 - \cos θ)}^{2} a^{2} + \sin^{2} θ b^{2}$ $\Rightarrow \frac{1 - \sin θ}{1 + \sin θ} + 2 \cos θ - (1 - μ^{2}) \cos^{2} θ = 1$ $\frac{1 - \frac{2 t}{1 + t^{2}}}{1 + \frac{2 t}{1 + t^{2}}} + 2 \times \frac{1 - t^{2}}{1 + t^{2}} - (1 - μ^{2}) {(\frac{1 - t^{2}}{1 + t^{2}})}^{2} = 1$ ${(\frac{1 - t}{1 + t})}^{2} + (\frac{1 - t^{2}}{1 + t^{2}}) [2 - (1 - μ^{2}) (\frac{1 - t^{2}}{1 + t^{2}})] = 1$ $μ^{4} + (\frac{1 - {(\frac{1 - μ^{2}}{1 + μ^{2}})}^{2}}{1 + {(\frac{1 - μ^{2}}{1 + μ^{2}})}^{2}}) [2 - (1 - μ^{2}) (\frac{1 - {(\frac{1 - μ^{2}}{1 + μ^{2}})}^{2}}{1 + {(\frac{1 - μ^{2}}{1 + μ^{2}})}^{2}})] = 1$ $μ^{4} + (\frac{2 μ^{2}}{1 + μ^{4}}) [2 - (1 - μ^{2}) (\frac{2 μ^{2}}{1 + μ^{4}})] = 1$ $μ^{4} + \frac{4 μ^{2} (1 - μ^{2} + 2 μ^{4})}{{(1 + μ^{4})}^{2}} = 1$ $4 μ^{2} (1 - μ^{2} + 2 μ^{4}) = (1 - μ^{4}) {(1 + μ^{4})}^{2}$ $μ^{12} + μ^{8} + 8 μ^{6} - 5 μ^{4} + 4 μ^{2} - 1 = 0$ $\Rightarrow μ \approx 0.554632$
	Commented by ajfour last updated on 16/Apr/20

	$T h a n k y o u S i r .$ $N i c e A n s w e r : μ ≊ 0.555$
	Commented by mr W last updated on 16/Apr/20

	${y o u}^{'} r e r i g h t, t h a n k s!$
	Answered by ajfour last updated on 16/Apr/20
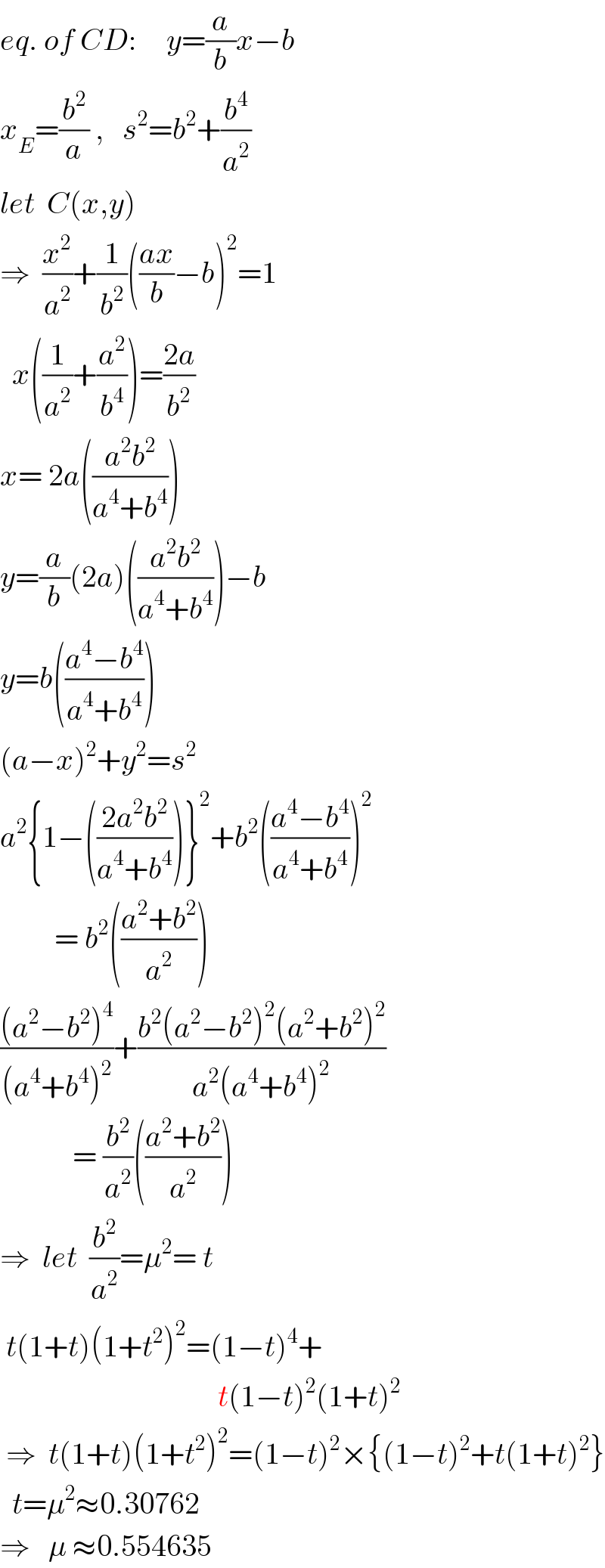
	$eq. of CD: y=(a/b)x−b x_E =(b^2 /a) , s^2 =b^2 +(b^4 /a^2 ) let C(x,y) ⇒ (x^2 /a^2 )+(1/b^2 )(((ax)/b)−b)^2 =1 x((1/a^2 )+(a^2 /b^4 ))=((2a)/b^2 ) x= 2a(((a^2 b^2 )/(a^4 +b^4 ))) y=(a/b)(2a)(((a^2 b^2 )/(a^4 +b^4 )))−b y=b(((a^4 −b^4 )/(a^4 +b^4 ))) (a−x)^2 +y^2 =s^2 a^2 {1−(((2a^2 b^2 )/(a^4 +b^4 )))}^2 +b^2 (((a^4 −b^4 )/(a^4 +b^4 )))^2 = b^2 (((a^2 +b^2 )/a^2 )) (((a^2 −b^2 )^4 )/((a^4 +b^4 )^2 ))+((b^2 (a^2 −b^2 )^2 (a^2 +b^2 )^2 )/(a^2 (a^4 +b^4 )^2 )) = (b^2 /a^2 )(((a^2 +b^2 )/a^2 )) ⇒ let (b^2 /a^2 )=μ^2 = t t(1+t)(1+t^2 )^2 =(1−t)^4 + t(1−t)^2 (1+t)^2 ⇒ t(1+t)(1+t^2 )^2 =(1−t)^2 ×{(1−t)^2 +t(1+t)^2 } t=μ^2 ≈0.30762 ⇒ μ ≈0.554635$
	$e q . o f C D : y = \frac{a}{b} x - b$ $x_{E} = \frac{b^{2}}{a}, s^{2} = b^{2} + \frac{b^{4}}{a^{2}}$ $l e t C (x, y)$ $\Rightarrow \frac{x^{2}}{a^{2}} + \frac{1}{b^{2}} {(\frac{a x}{b} - b)}^{2} = 1$ $x (\frac{1}{a^{2}} + \frac{a^{2}}{b^{4}}) = \frac{2 a}{b^{2}}$ $x = 2 a (\frac{a^{2} b^{2}}{a^{4} + b^{4}})$ $y = \frac{a}{b} (2 a) (\frac{a^{2} b^{2}}{a^{4} + b^{4}}) - b$ $y = b (\frac{a^{4} - b^{4}}{a^{4} + b^{4}})$ ${(a - x)}^{2} + y^{2} = s^{2}$ $a^{2} {1 - (\frac{2 a^{2} b^{2}}{a^{4} + b^{4}})}^{2} + b^{2} {(\frac{a^{4} - b^{4}}{a^{4} + b^{4}})}^{2}$ $= b^{2} (\frac{a^{2} + b^{2}}{a^{2}})$ $\frac{{(a^{2} - b^{2})}^{4}}{{(a^{4} + b^{4})}^{2}} + \frac{b^{2} {(a^{2} - b^{2})}^{2} {(a^{2} + b^{2})}^{2}}{a^{2} {(a^{4} + b^{4})}^{2}}$ $= \frac{b^{2}}{a^{2}} (\frac{a^{2} + b^{2}}{a^{2}})$ $\Rightarrow l e t \frac{b^{2}}{a^{2}} = μ^{2} = t$ $t (1 + t) {(1 + t^{2})}^{2} = {(1 - t)}^{4} +$ $t {(1 - t)}^{2} {(1 + t)}^{2}$ $\Rightarrow t (1 + t) {(1 + t^{2})}^{2} = {(1 - t)}^{2} \times {{(1 - t)}^{2} + t {(1 + t)}^{2}}$ $t = μ^{2} \approx 0.30762$ $\Rightarrow μ \approx 0.554635$
	Commented by ajfour last updated on 16/Apr/20

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum