
Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 89205 by jagoll last updated on 16/Apr/20
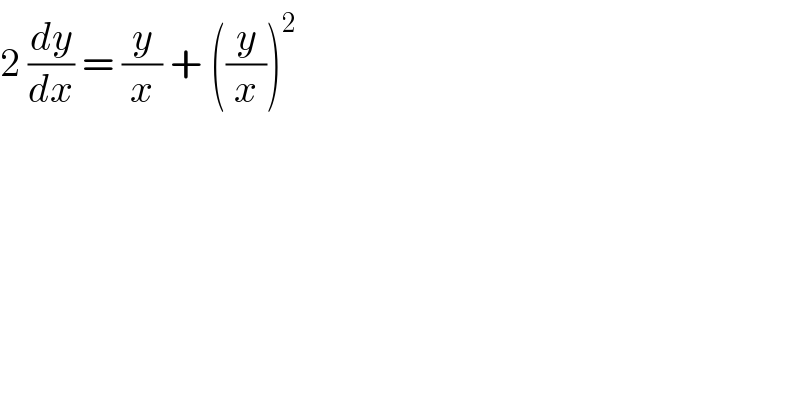
Commented by john santu last updated on 16/Apr/20
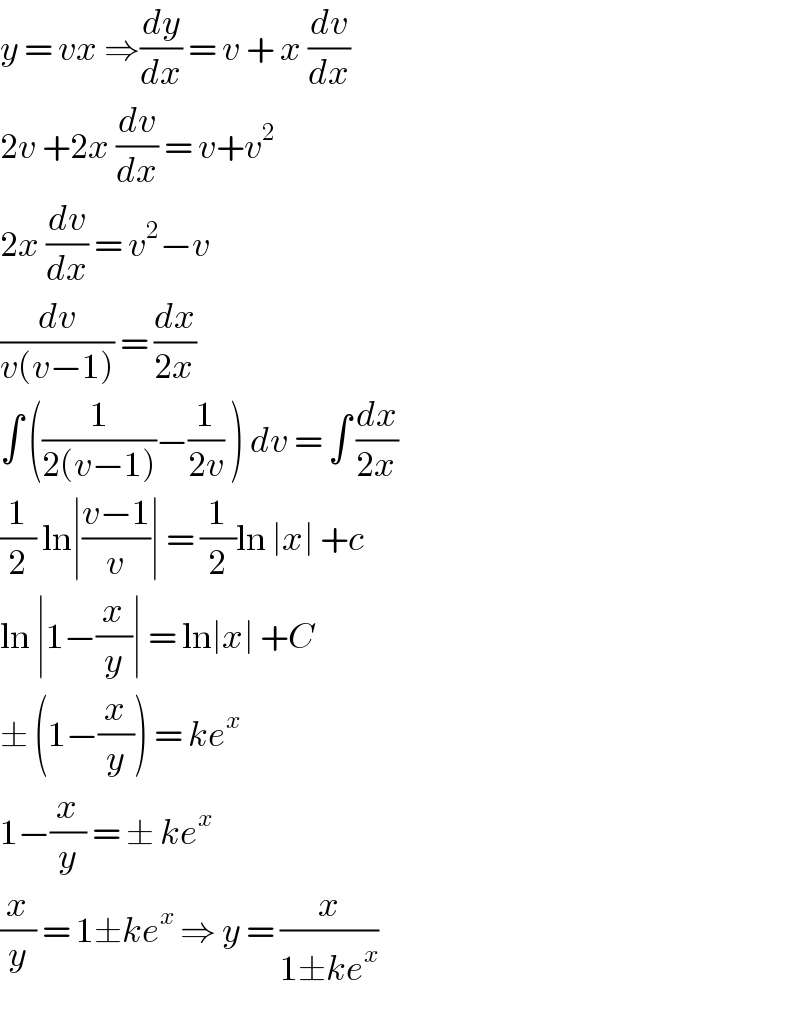
Answered by 242242864 last updated on 16/Apr/20
![let u = (y/x) ⇒y=ux (dy/dx)=u+x(du/dx) 2[u+x(du/dx)]=u+u^2 2u+2x(du/dc) = u+u^2 2x(du/dx)=u^2 −u 2xdu=(u^2 −u)dx ((2du)/((u^2 −u)))=(dx/x) 2∫(du/((u^2 −u)))=∫(dx/x) consider (1/((u^2 −u))) to be change to partial fraction, (1/((u^2 −u)))= (1/((u+1)(u−1))) ⇒(1/((u+1)(u−1))) = (A/((u+1)))+(B/((u−1))) 1= A(u−1)+B(u+1) 1= Au−A+Bu+B 1=u(A+B)+B−A B−A=1.........(i) A+B=0..........(ii) ⇒A= −(1/2), B = (1/2) ⇒∫(1/((u^2 −1)))du = (1/2)∫(du/((u−1)))−(1/2)∫(du/((u+1))) = ∫(dx/x) (1/2)ln(u−1)−(1/2)ln(u+1)=lnx+C (1/2)ln[((u−1)/(u+1))]= lnx+C (1/2)ln[((y−x)/(y+x))] = lnx+C](Q89235.png)
| ||
Question and Answers Forum | ||
Previous in Differential Equation Next in Differential Equation | ||
Question Number 89205 by jagoll last updated on 16/Apr/20 | ||
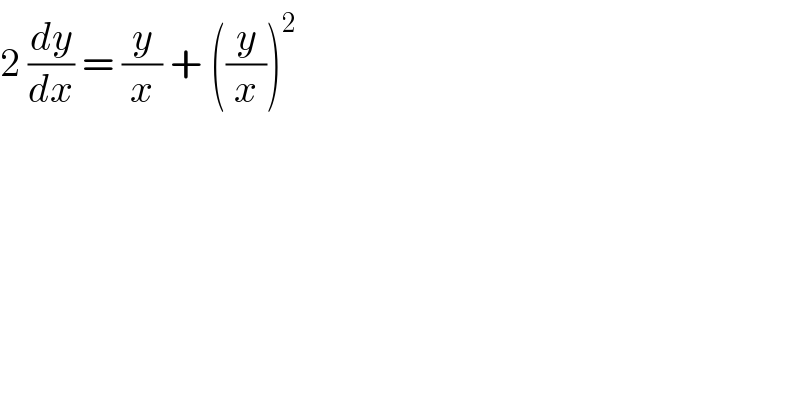 | ||
Commented by john santu last updated on 16/Apr/20 | ||
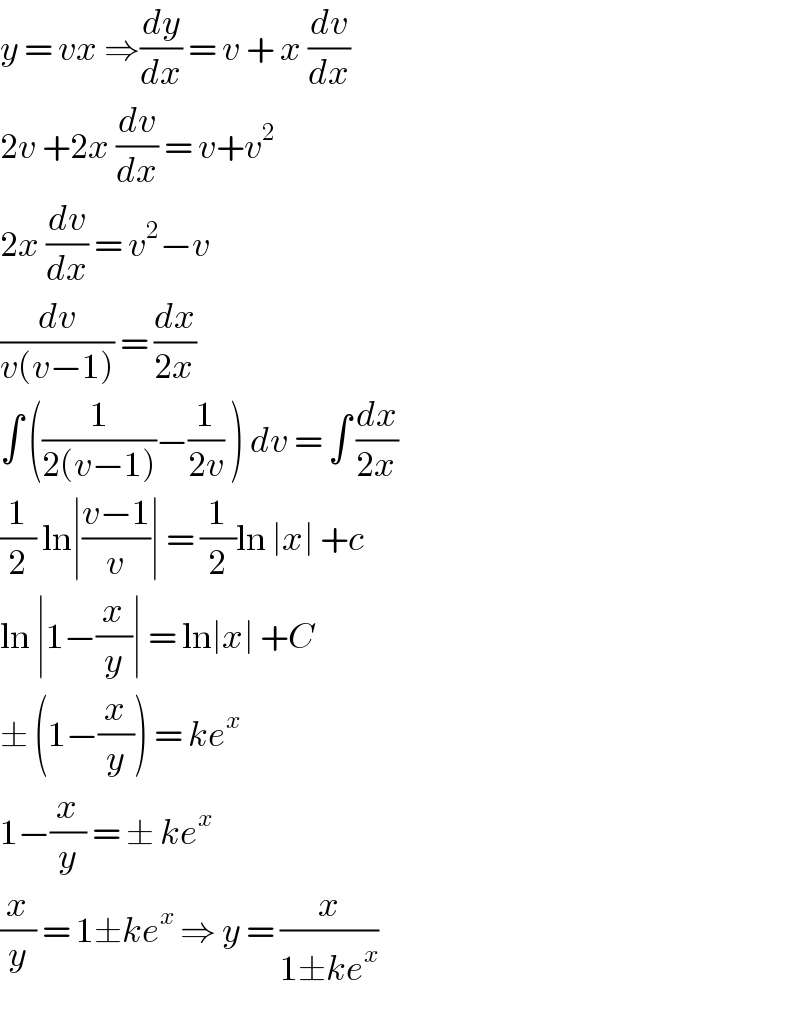 | ||
Answered by 242242864 last updated on 16/Apr/20 | ||
![let u = (y/x) ⇒y=ux (dy/dx)=u+x(du/dx) 2[u+x(du/dx)]=u+u^2 2u+2x(du/dc) = u+u^2 2x(du/dx)=u^2 −u 2xdu=(u^2 −u)dx ((2du)/((u^2 −u)))=(dx/x) 2∫(du/((u^2 −u)))=∫(dx/x) consider (1/((u^2 −u))) to be change to partial fraction, (1/((u^2 −u)))= (1/((u+1)(u−1))) ⇒(1/((u+1)(u−1))) = (A/((u+1)))+(B/((u−1))) 1= A(u−1)+B(u+1) 1= Au−A+Bu+B 1=u(A+B)+B−A B−A=1.........(i) A+B=0..........(ii) ⇒A= −(1/2), B = (1/2) ⇒∫(1/((u^2 −1)))du = (1/2)∫(du/((u−1)))−(1/2)∫(du/((u+1))) = ∫(dx/x) (1/2)ln(u−1)−(1/2)ln(u+1)=lnx+C (1/2)ln[((u−1)/(u+1))]= lnx+C (1/2)ln[((y−x)/(y+x))] = lnx+C](Q89235.png) | ||
| ||