
Question and Answers Forum
Question Number 89273 by Ar Brandon last updated on 16/Apr/20
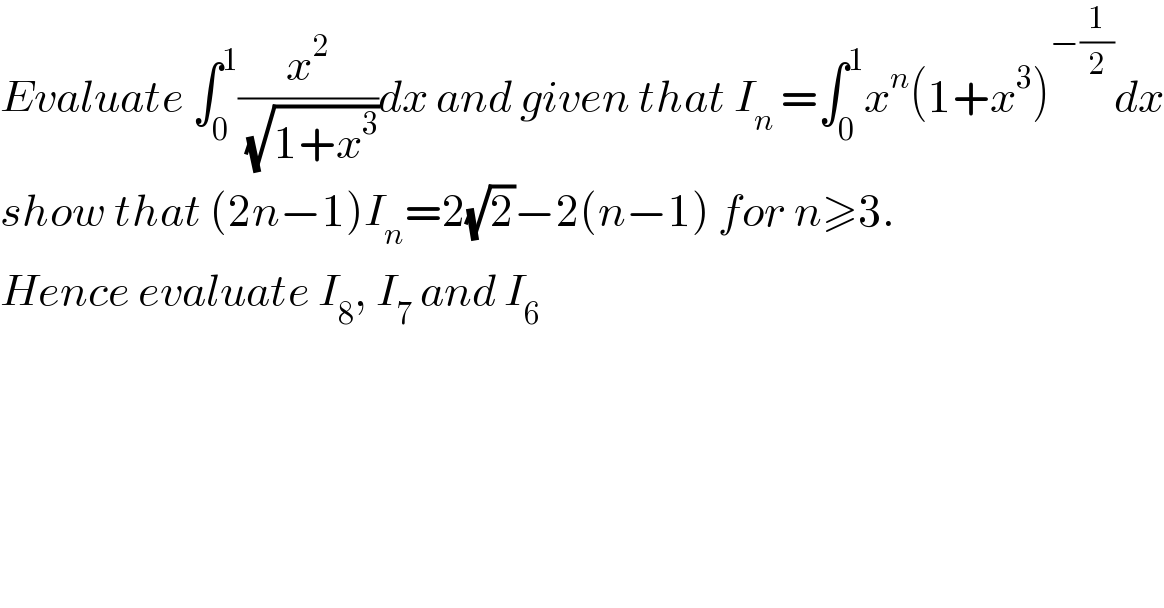
Answered by 675480065 last updated on 17/Apr/20
![evaluating the intergral: ∫_0 ^1 (x^2 /(√(1+x^3 )))dx=J Let u=x^3 +1 ⇒du=3x^2 dx ⇒ x^2 dx=(1/3)du. substitute above we get... J=(1/3)∫_0 ^1 u^(−(1/2)) du =(1/6)(√u), but u=(√(x^3 +1)). J=(1/6)((√(√(x^3 +1))))]_0 ^(1 ) =(1/6){(√(√2))−1} Also: I_n =∫_0 ^1 x^n (1+x^3 )^((−1)/2) dx. let u=(1+x^3 )^(−(1/2)) dv=x^n dx ⇒(du/dx)=−((3x^2 )/2)(1+x^3 )^(−(3/2)) v=(x^(n+1) /((n+1))).](Q89375.png)
| ||
Question and Answers Forum | ||
Question Number 89273 by Ar Brandon last updated on 16/Apr/20 | ||
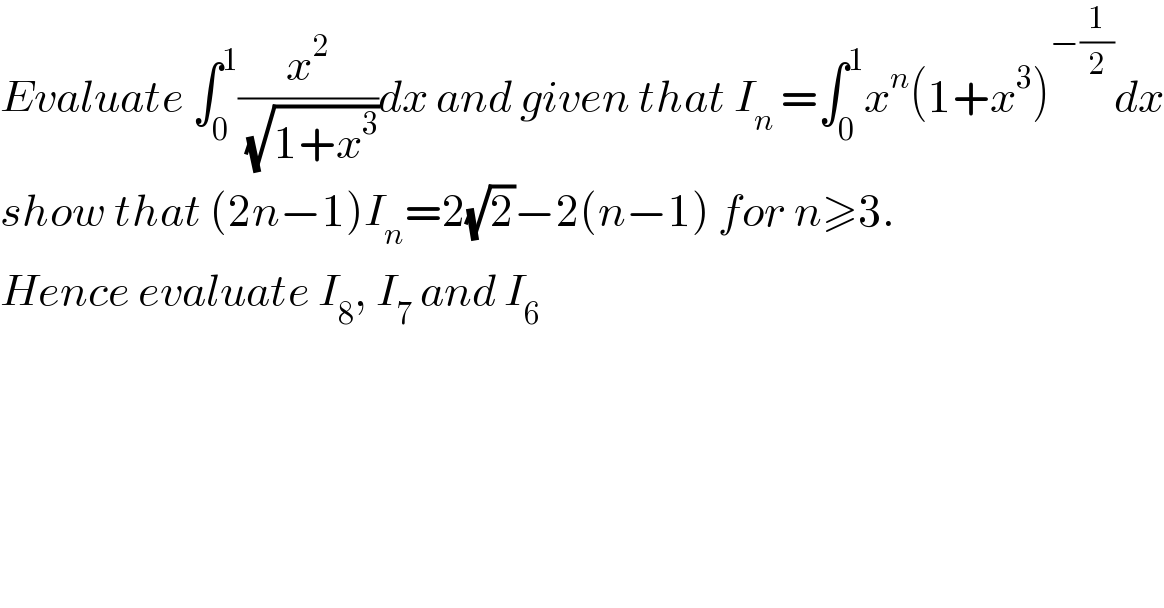 | ||
Answered by 675480065 last updated on 17/Apr/20 | ||
![evaluating the intergral: ∫_0 ^1 (x^2 /(√(1+x^3 )))dx=J Let u=x^3 +1 ⇒du=3x^2 dx ⇒ x^2 dx=(1/3)du. substitute above we get... J=(1/3)∫_0 ^1 u^(−(1/2)) du =(1/6)(√u), but u=(√(x^3 +1)). J=(1/6)((√(√(x^3 +1))))]_0 ^(1 ) =(1/6){(√(√2))−1} Also: I_n =∫_0 ^1 x^n (1+x^3 )^((−1)/2) dx. let u=(1+x^3 )^(−(1/2)) dv=x^n dx ⇒(du/dx)=−((3x^2 )/2)(1+x^3 )^(−(3/2)) v=(x^(n+1) /((n+1))).](Q89375.png) | ||
| ||