
Question and Answers Forum
Question Number 89286 by M±th+et£s last updated on 16/Apr/20
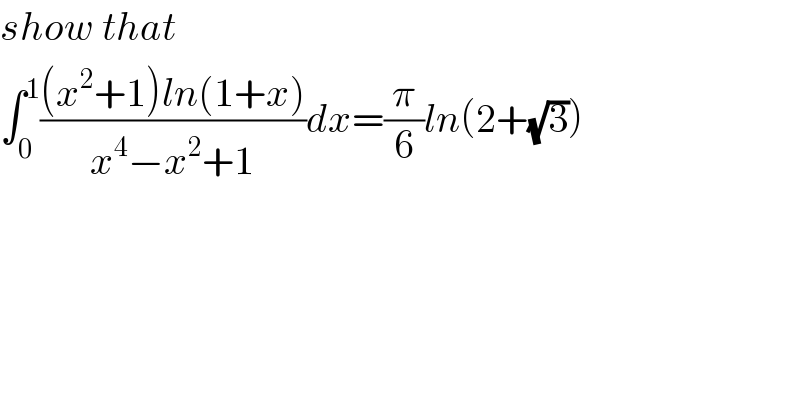
Answered by TANMAY PANACEA. last updated on 16/Apr/20
![∫((1+(1/x^2 ))/(x^2 +(1/x^2 )−1)).ln(1+x)dx ln(1+x)∫((d(x−(1/x))^ )/((x−(1/x))^2 +1))−∫[(1/(1+x))∫((d(x−(1/x)))/((x−(1/x))^2 +1))dx]dx ln(1+x).tan^(−1) (x−(1/x))−∫((tan^(−1) (x−(1/x)))/(1+x))dx wait...](Q89296.png)
Commented by M±th+et£s last updated on 16/Apr/20

Answered by M±th+et£s last updated on 16/Apr/20

| ||
Question and Answers Forum | ||
Question Number 89286 by M±th+et£s last updated on 16/Apr/20 | ||
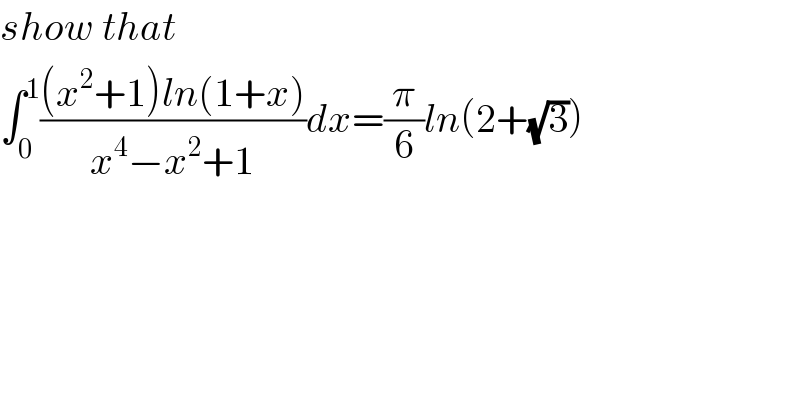 | ||
Answered by TANMAY PANACEA. last updated on 16/Apr/20 | ||
![∫((1+(1/x^2 ))/(x^2 +(1/x^2 )−1)).ln(1+x)dx ln(1+x)∫((d(x−(1/x))^ )/((x−(1/x))^2 +1))−∫[(1/(1+x))∫((d(x−(1/x)))/((x−(1/x))^2 +1))dx]dx ln(1+x).tan^(−1) (x−(1/x))−∫((tan^(−1) (x−(1/x)))/(1+x))dx wait...](Q89296.png) | ||
| ||
Commented by M±th+et£s last updated on 16/Apr/20 | ||
 | ||
Answered by M±th+et£s last updated on 16/Apr/20 | ||
 | ||