Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 89317 by abdomathmax last updated on 16/Apr/20

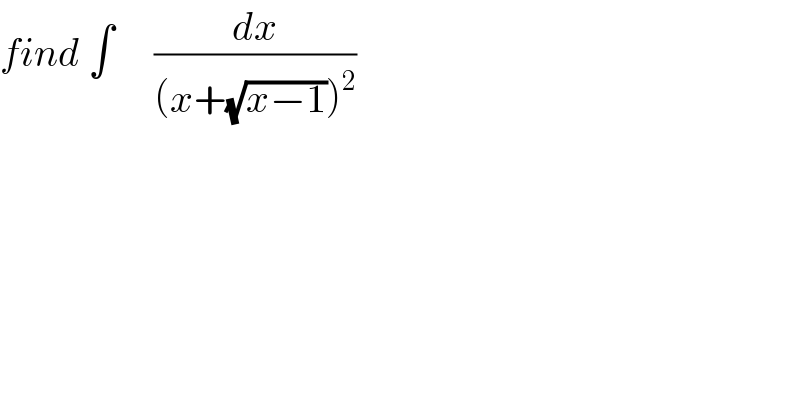
find ∫ (dx/((x+(√(x−1)))^2 ))

$${find}\:\int\:\:\:\:\:\frac{{dx}}{\left({x}+\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} } \\ $$

Commented by mathmax by abdo last updated on 17/Apr/20

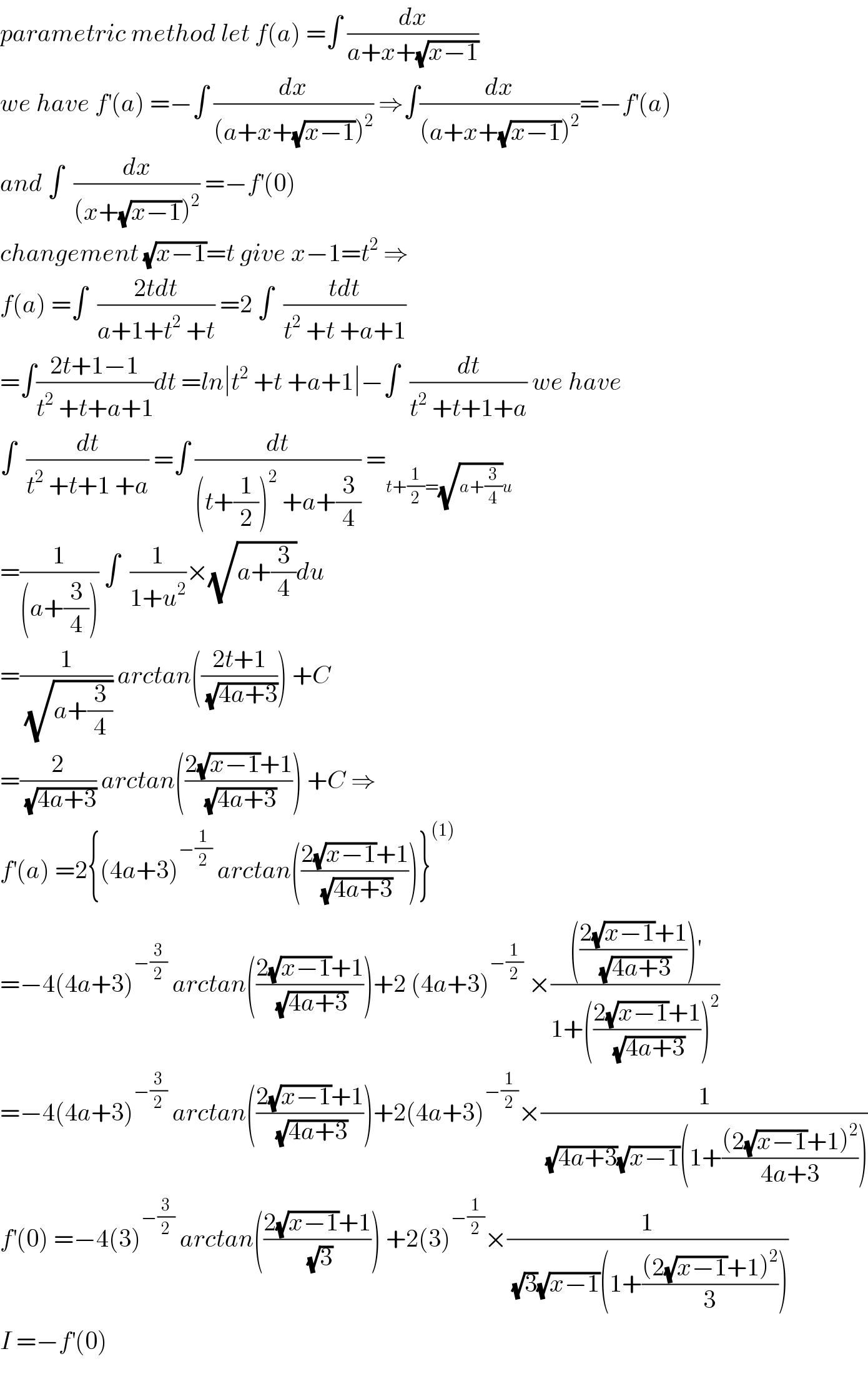
parametric method let f(a) =∫ (dx/(a+x+(√(x−1)))) we have f^′ (a) =−∫ (dx/((a+x+(√(x−1)))^2 )) ⇒∫(dx/((a+x+(√(x−1)))^2 ))=−f^′ (a) and ∫ (dx/((x+(√(x−1)))^2 )) =−f^′ (0) changement (√(x−1))=t give x−1=t^2 ⇒ f(a) =∫ ((2tdt)/(a+1+t^2 +t)) =2 ∫ ((tdt)/(t^2 +t +a+1)) =∫((2t+1−1)/(t^2 +t+a+1))dt =ln∣t^2 +t +a+1∣−∫ (dt/(t^2 +t+1+a)) we have ∫ (dt/(t^2 +t+1 +a)) =∫ (dt/((t+(1/2))^2 +a+(3/4))) =_(t+(1/2)=(√(a+(3/4)))u) =(1/((a+(3/4)))) ∫ (1/(1+u^2 ))×(√(a+(3/4)))du =(1/(√(a+(3/4)))) arctan(((2t+1)/(√(4a+3)))) +C =(2/(√(4a+3))) arctan(((2(√(x−1))+1)/(√(4a+3)))) +C ⇒ f^′ (a) =2{(4a+3)^(−(1/2)) arctan(((2(√(x−1))+1)/(√(4a+3))))}^((1)) =−4(4a+3)^(−(3/2)) arctan(((2(√(x−1))+1)/(√(4a+3))))+2 (4a+3)^(−(1/2)) ×(((((2(√(x−1))+1)/(√(4a+3))))^′ )/(1+(((2(√(x−1))+1)/(√(4a+3))))^2 )) =−4(4a+3)^(−(3/2)) arctan(((2(√(x−1))+1)/(√(4a+3))))+2(4a+3)^(−(1/2)) ×(1/((√(4a+3))(√(x−1))(1+(((2(√(x−1))+1)^2 )/(4a+3))))) f^′ (0) =−4(3)^(−(3/2)) arctan(((2(√(x−1))+1)/(√3))) +2(3)^(−(1/2)) ×(1/((√3)(√(x−1))(1+(((2(√(x−1))+1)^2 )/3)))) I =−f^′ (0)

$${parametric}\:{method}\:{let}\:{f}\left({a}\right)\:=\int\:\frac{{dx}}{{a}+{x}+\sqrt{{x}−\mathrm{1}}} \\ $$$${we}\:{have}\:{f}^{'} \left({a}\right)\:=−\int\:\frac{{dx}}{\left({a}+{x}+\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} }\:\Rightarrow\int\frac{{dx}}{\left({a}+{x}+\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} }=−{f}^{'} \left({a}\right) \\ $$$${and}\:\int\:\:\frac{{dx}}{\left({x}+\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} }\:=−{f}^{'} \left(\mathrm{0}\right) \\ $$$${changement}\:\sqrt{{x}−\mathrm{1}}={t}\:{give}\:{x}−\mathrm{1}={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${f}\left({a}\right)\:=\int\:\:\frac{\mathrm{2}{tdt}}{{a}+\mathrm{1}+{t}^{\mathrm{2}} \:+{t}}\:=\mathrm{2}\:\int\:\:\frac{{tdt}}{{t}^{\mathrm{2}} \:+{t}\:+{a}+\mathrm{1}} \\ $$$$=\int\frac{\mathrm{2}{t}+\mathrm{1}−\mathrm{1}}{{t}^{\mathrm{2}} \:+{t}+{a}+\mathrm{1}}{dt}\:={ln}\mid{t}^{\mathrm{2}} \:+{t}\:+{a}+\mathrm{1}\mid−\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}+{a}}\:{we}\:{have} \\ $$$$\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}\:+{a}}\:=\int\:\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+{a}+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{t}+\frac{\mathrm{1}}{\mathrm{2}}=\sqrt{{a}+\frac{\mathrm{3}}{\mathrm{4}}}{u}} \\ $$$$=\frac{\mathrm{1}}{\left({a}+\frac{\mathrm{3}}{\mathrm{4}}\right)}\:\int\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }×\sqrt{{a}+\frac{\mathrm{3}}{\mathrm{4}}}{du} \\ $$$$=\frac{\mathrm{1}}{\sqrt{{a}+\frac{\mathrm{3}}{\mathrm{4}}}}\:{arctan}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}}\right)\:+{C} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}}\right)\:+{C}\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)\:=\mathrm{2}\left\{\left(\mathrm{4}{a}+\mathrm{3}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{arctan}\left(\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=−\mathrm{4}\left(\mathrm{4}{a}+\mathrm{3}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{arctan}\left(\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}}\right)+\mathrm{2}\:\left(\mathrm{4}{a}+\mathrm{3}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:×\frac{\left(\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}}\right)^{'} }{\mathrm{1}+\left(\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}}\right)^{\mathrm{2}} } \\ $$$$=−\mathrm{4}\left(\mathrm{4}{a}+\mathrm{3}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{arctan}\left(\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}}\right)+\mathrm{2}\left(\mathrm{4}{a}+\mathrm{3}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} ×\frac{\mathrm{1}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}\sqrt{{x}−\mathrm{1}}\left(\mathrm{1}+\frac{\left(\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}{a}+\mathrm{3}}\right)} \\ $$$${f}^{'} \left(\mathrm{0}\right)\:=−\mathrm{4}\left(\mathrm{3}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{arctan}\left(\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\:+\mathrm{2}\left(\mathrm{3}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} ×\frac{\mathrm{1}}{\sqrt{\mathrm{3}}\sqrt{{x}−\mathrm{1}}\left(\mathrm{1}+\frac{\left(\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}}\right)} \\ $$$${I}\:=−{f}^{'} \left(\mathrm{0}\right) \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 17/Apr/20

forgive f^′ (a) =(1/(t^2 +t+a+1)) +4(4a+3)^(−(3/2)) arctan(((2(√(x−1))+1)/(√(4a+3)))) −2(4a+3)^(−(1/2)) ×(1/((√(4a+3))(√(x−1))(1+(((2(√(x−1))+1)^2 )/(4a+3))))) ⇒ f^′ (0) =(1/(t^2 +t+1)) +4(3)^(−(3/2)) arctan(((2(√(x−1))+1)/(√3))) −2(3)^(−(1/2)) ×(1/((√3)(√(x−1))(1+(((2(√(x−1))+1)^2 )/3))))

$${forgive}\:{f}^{'} \left({a}\right)\:=\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+{t}+{a}+\mathrm{1}}\:+\mathrm{4}\left(\mathrm{4}{a}+\mathrm{3}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{arctan}\left(\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}}\right) \\ $$$$−\mathrm{2}\left(\mathrm{4}{a}+\mathrm{3}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} ×\frac{\mathrm{1}}{\sqrt{\mathrm{4}{a}+\mathrm{3}}\sqrt{{x}−\mathrm{1}}\left(\mathrm{1}+\frac{\left(\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}{a}+\mathrm{3}}\right)}\:\Rightarrow \\ $$$${f}^{'} \left(\mathrm{0}\right)\:=\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}\:+\mathrm{4}\left(\mathrm{3}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{arctan}\left(\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right) \\ $$$$−\mathrm{2}\left(\mathrm{3}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} ×\frac{\mathrm{1}}{\sqrt{\mathrm{3}}\sqrt{{x}−\mathrm{1}}\left(\mathrm{1}+\frac{\left(\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}}\right)} \\ $$

Answered by MJS last updated on 16/Apr/20

∫(dx/((x+(√(x−1)))^2 ))= [t=(√(x−1)) → dx=2(√(x−1))dt] =2∫(t/((t^2 +t+1)^2 ))dt= [Ostrogradski] =−((2(t+2))/(3(t^2 +t+1)))−(2/3)∫(dt/(t^2 +t+1))= =−((2(t+2))/(3(t^2 +t+1)))−((4(√3))/9)arctan ((2t+1)/(√3)) = =−((2(2+(√(x−1))))/(3(x+(√(x−1)))))−((4(√3))/9)arctan ((1+2(√(x−1)))/(√3)) +C

$$\int\frac{{dx}}{\left({x}+\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}−\mathrm{1}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}−\mathrm{1}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}}{\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=−\frac{\mathrm{2}\left({t}+\mathrm{2}\right)}{\mathrm{3}\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}= \\ $$$$=−\frac{\mathrm{2}\left({t}+\mathrm{2}\right)}{\mathrm{3}\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}−\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\mathrm{2}{t}+\mathrm{1}}{\sqrt{\mathrm{3}}}\:= \\ $$$$=−\frac{\mathrm{2}\left(\mathrm{2}+\sqrt{{x}−\mathrm{1}}\right)}{\mathrm{3}\left({x}+\sqrt{{x}−\mathrm{1}}\right)}−\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\mathrm{1}+\mathrm{2}\sqrt{{x}−\mathrm{1}}}{\sqrt{\mathrm{3}}}\:+{C} \\ $$

Commented by mathmax by abdo last updated on 17/Apr/20

thank you sir.

$${thank}\:{you}\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com