Question and Answers Forum
Question Number 89318 by M±th+et£s last updated on 16/Apr/20
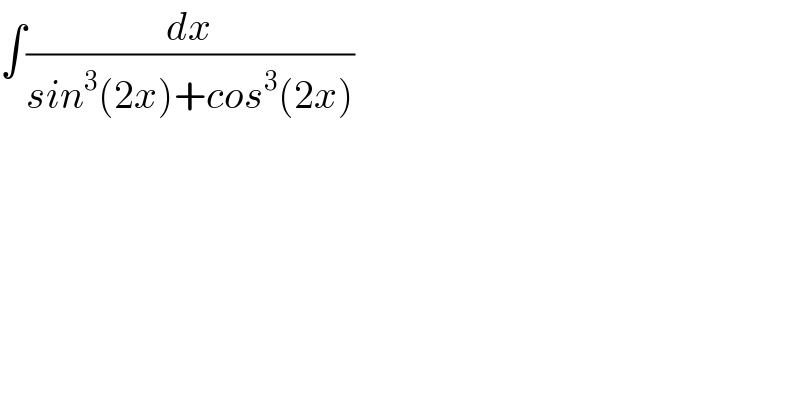
Answered by MJS last updated on 16/Apr/20
![∫(dx/(sin^3 2x +cos^3 2x))= [t=tan x → dx=cos^2 x dt] =−∫(((t^2 +1)^2 )/((t^2 −2t−1)(t^2 +(1−(√3))t+2−(√3))(t^2 +(1+(√3))t+2+(√3))))dt= =−(2/3)∫(dt/(t^2 −2t−1))+ −((1−(√3))/6)∫(dt/(t^2 +(1−(√3))t+2−(√3)))− −((1+(√3))/6)∫(dt/(t^2 +(1+(√3))t+2+(√3)))= [now use formulas] =((√2)/6)ln ((t−1+(√2))/(t−1−(√2))) +(1/3)(arctan ((1+(√3))t−1) +arctan ((1−(√3))t−1)) with t=tan x](Q89330.png)
Commented by M±th+et£s last updated on 16/Apr/20

Answered by M±th+et£s last updated on 17/Apr/20
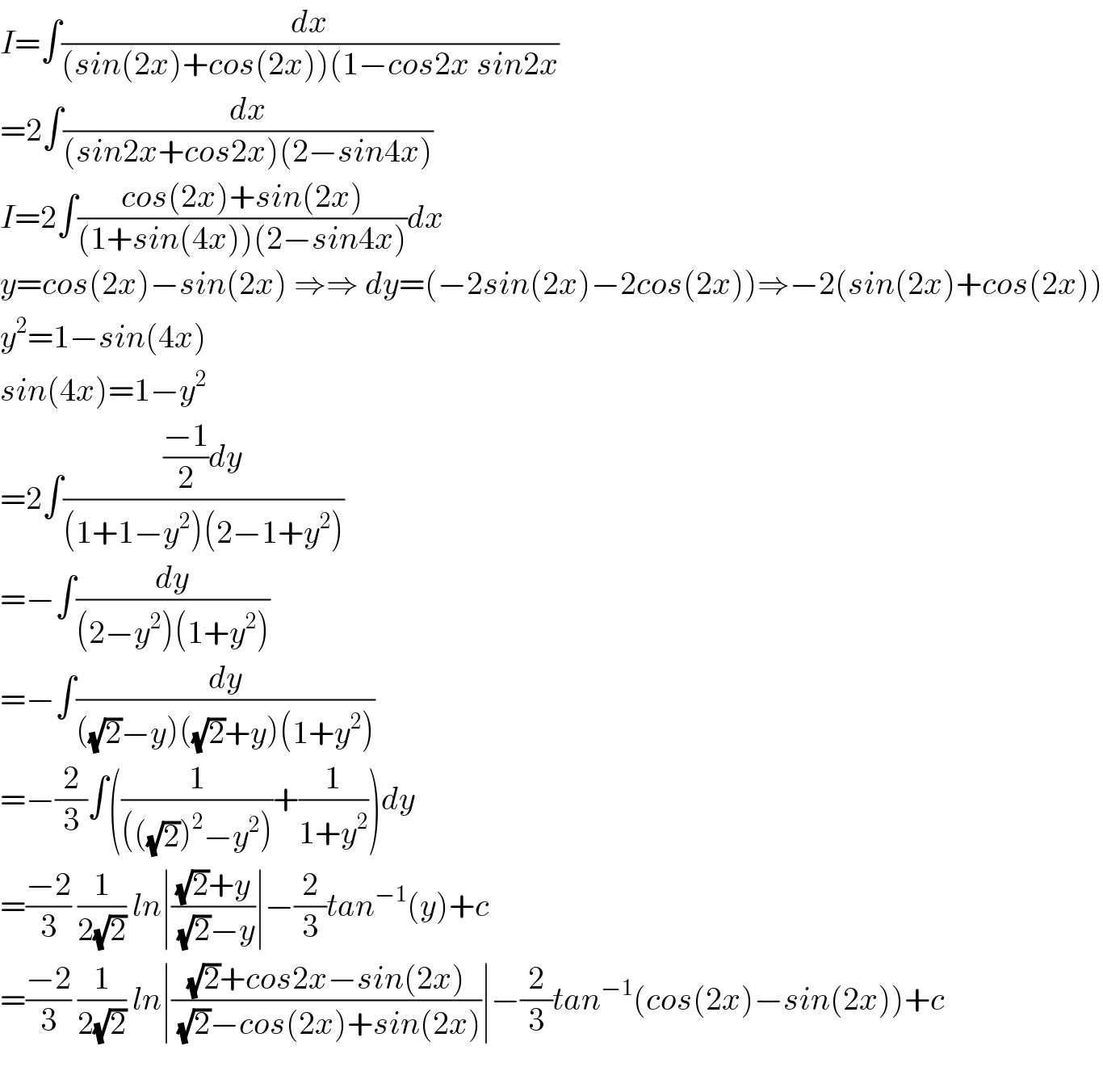
Commented by MJS last updated on 17/Apr/20
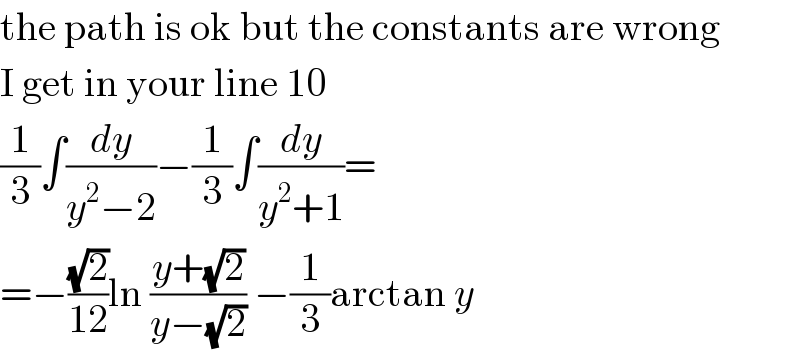
Commented by M±th+et£s last updated on 17/Apr/20
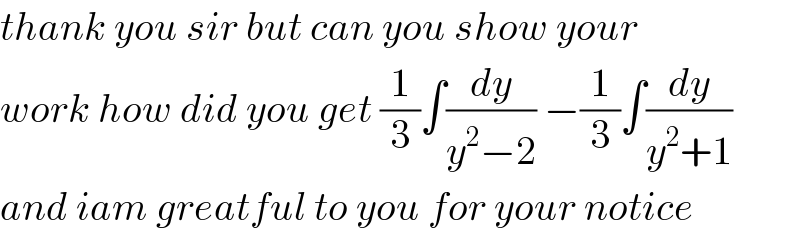
Commented by M±th+et£s last updated on 17/Apr/20
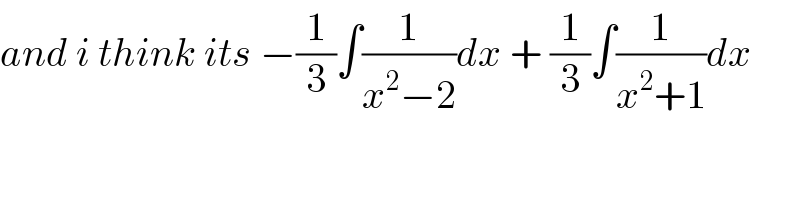
Commented by M±th+et£s last updated on 17/Apr/20