Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 89382 by M±th+et£s last updated on 17/Apr/20

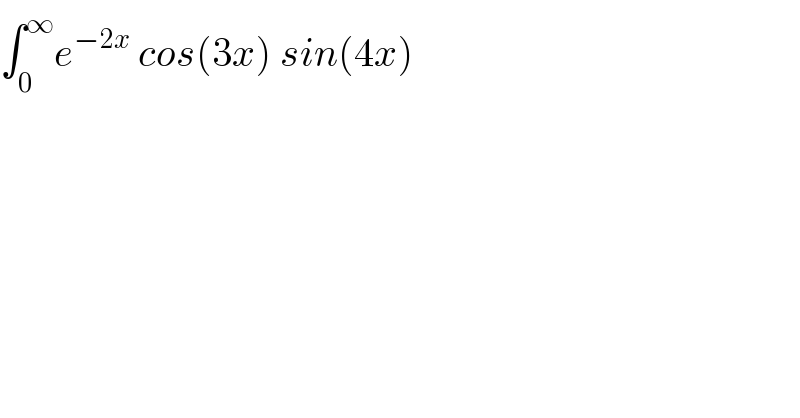
∫_0 ^∞ e^(−2x) cos(3x) sin(4x)

$$\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} \:{cos}\left(\mathrm{3}{x}\right)\:{sin}\left(\mathrm{4}{x}\right) \\ $$

Commented by mathmax by abdo last updated on 17/Apr/20

cos(3x)sin(4x) =cos(3x)cos((π/2)−4x) =(1/2){cos(3x+(π/2)−4x) +cos(3x−(π/2)+4x)} =(1/2){cos((π/2)−x) +cos(7x−(π/2))} =(1/2){sinx +sin(7x)} ⇒ ∫_0 ^∞ e^(−2x) cos(3x)sin(4x)dx =(1/2)∫_0 ^∞ e^(−2x) sinx+(1/2)∫_0 ^∞ e^(−2x) sin(7x)dx ∫_0 ^∞ e^(−2x) sinx dx =Im(∫_0 ^∞ e^(−2x +ix) dx) ∫_0 ^∞ e^((−2+i)x) dx =[(1/(−2+i))e^((−2+i)x) ]_0 ^(+∞) =(1/(−2+i))(−1) =(1/(2−i)) =((2+i)/5) ⇒∫_0 ^∞ e^(−2x) sinxdx =(1/5) ∫_0 ^∞ e^(−2x) sin(7x)dx =Im(∫_0 ^∞ e^(−2x+7ix) dx) ∫_0 ^∞ e^((−2+7i)x) dx =[(1/(−2+7i))e^((−2+7i)x) ]_0 ^(+∞) =(1/(−2+7i))(−1) =(1/(2−7i)) =((2+7i)/(4+49)) =((2+7i)/(53)) ⇒∫_0 ^∞ e^(−2x) sin(7x)dx=(7/(53)) ⇒ I =(1/(10)) +(7/(106)) =((106+70)/(1060)) =((176)/(1060)) =...

$${cos}\left(\mathrm{3}{x}\right){sin}\left(\mathrm{4}{x}\right)\:={cos}\left(\mathrm{3}{x}\right){cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{4}{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left(\mathrm{3}{x}+\frac{\pi}{\mathrm{2}}−\mathrm{4}{x}\right)\:+{cos}\left(\mathrm{3}{x}−\frac{\pi}{\mathrm{2}}+\mathrm{4}{x}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\:+{cos}\left(\mathrm{7}{x}−\frac{\pi}{\mathrm{2}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{sinx}\:+{sin}\left(\mathrm{7}{x}\right)\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{x}} \:{cos}\left(\mathrm{3}{x}\right){sin}\left(\mathrm{4}{x}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} \:{sinx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} \:{sin}\left(\mathrm{7}{x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{x}} \:{sinx}\:{dx}\:={Im}\left(\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}\:+{ix}} {dx}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−\mathrm{2}+{i}\right){x}} \:{dx}\:=\left[\frac{\mathrm{1}}{−\mathrm{2}+{i}}{e}^{\left(−\mathrm{2}+{i}\right){x}} \right]_{\mathrm{0}} ^{+\infty} \:=\frac{\mathrm{1}}{−\mathrm{2}+{i}}\left(−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}−{i}}\:=\frac{\mathrm{2}+{i}}{\mathrm{5}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{x}} \:{sinxdx}\:=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{x}} {sin}\left(\mathrm{7}{x}\right){dx}\:={Im}\left(\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}+\mathrm{7}{ix}} {dx}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−\mathrm{2}+\mathrm{7}{i}\right){x}} \:{dx}\:=\left[\frac{\mathrm{1}}{−\mathrm{2}+\mathrm{7}{i}}{e}^{\left(−\mathrm{2}+\mathrm{7}{i}\right){x}} \right]_{\mathrm{0}} ^{+\infty} \:=\frac{\mathrm{1}}{−\mathrm{2}+\mathrm{7}{i}}\left(−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}−\mathrm{7}{i}}\:=\frac{\mathrm{2}+\mathrm{7}{i}}{\mathrm{4}+\mathrm{49}}\:=\frac{\mathrm{2}+\mathrm{7}{i}}{\mathrm{53}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} {sin}\left(\mathrm{7}{x}\right){dx}=\frac{\mathrm{7}}{\mathrm{53}}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{10}}\:+\frac{\mathrm{7}}{\mathrm{106}}\:=\frac{\mathrm{106}+\mathrm{70}}{\mathrm{1060}}\:=\frac{\mathrm{176}}{\mathrm{1060}}\:=... \\ $$

Commented by mathmax by abdo last updated on 18/Apr/20

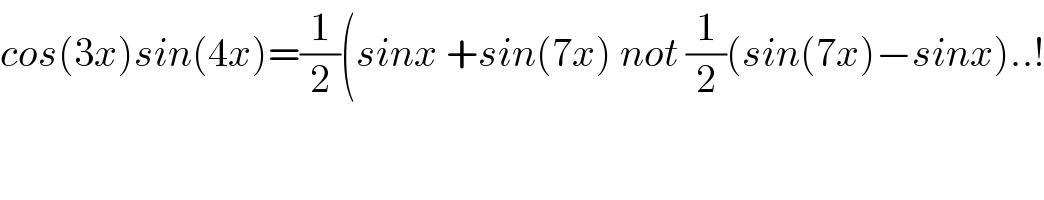
cos(3x)sin(4x)=(1/2)(sinx +sin(7x) not (1/2)(sin(7x)−sinx)..!

$${cos}\left(\mathrm{3}{x}\right){sin}\left(\mathrm{4}{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({sinx}\:+{sin}\left(\mathrm{7}{x}\right)\:{not}\:\frac{\mathrm{1}}{\mathrm{2}}\left({sin}\left(\mathrm{7}{x}\right)−{sinx}\right)..!\right. \\ $$

Answered by TANMAY PANACEA. last updated on 17/Apr/20

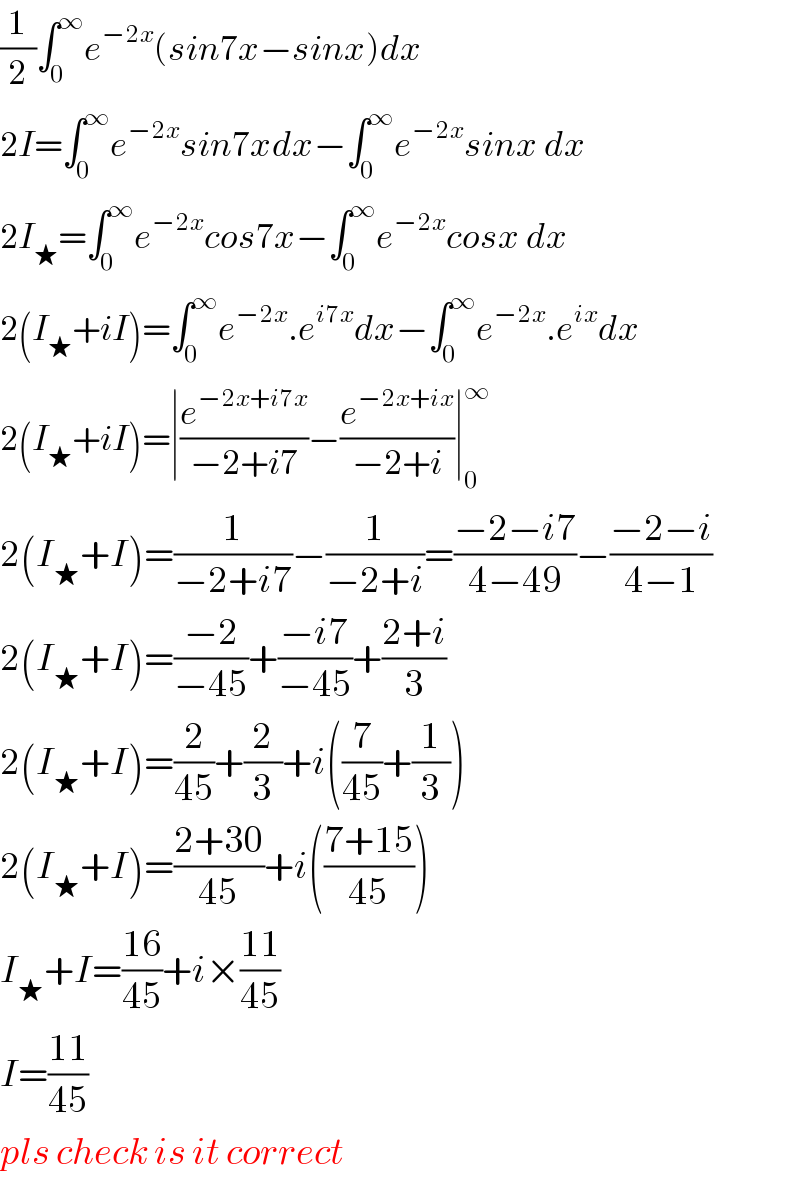
(1/2)∫_0 ^∞ e^(−2x) (sin7x−sinx)dx 2I=∫_0 ^∞ e^(−2x) sin7xdx−∫_0 ^∞ e^(−2x) sinx dx 2I_★ =∫_0 ^∞ e^(−2x) cos7x−∫_0 ^∞ e^(−2x) cosx dx 2(I_★ +iI)=∫_0 ^∞ e^(−2x) .e^(i7x) dx−∫_0 ^∞ e^(−2x) .e^(ix) dx 2(I_★ +iI)=∣(e^(−2x+i7x) /(−2+i7))−(e^(−2x+ix) /(−2+i))∣_0 ^∞ 2(I_★ +I)=(1/(−2+i7))−(1/(−2+i))=((−2−i7)/(4−49))−((−2−i)/(4−1)) 2(I_★ +I)=((−2)/(−45))+((−i7)/(−45))+((2+i)/3) 2(I_★ +I)=(2/(45))+(2/3)+i((7/(45))+(1/3)) 2(I_★ +I)=((2+30)/(45))+i(((7+15)/(45))) I_★ +I=((16)/(45))+i×((11)/(45)) I=((11)/(45)) pls check is it correct

$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} \left({sin}\mathrm{7}{x}−{sinx}\right){dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} {sin}\mathrm{7}{xdx}−\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} {sinx}\:{dx} \\ $$$$\mathrm{2}{I}_{\bigstar} =\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} {cos}\mathrm{7}{x}−\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} {cosx}\:{dx} \\ $$$$\mathrm{2}\left({I}_{\bigstar} +{iI}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} .{e}^{{i}\mathrm{7}{x}} {dx}−\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} .{e}^{{ix}} {dx} \\ $$$$\mathrm{2}\left({I}_{\bigstar} +{iI}\right)=\mid\frac{{e}^{−\mathrm{2}{x}+{i}\mathrm{7}{x}} }{−\mathrm{2}+{i}\mathrm{7}}−\frac{{e}^{−\mathrm{2}{x}+{ix}} }{−\mathrm{2}+{i}}\mid_{\mathrm{0}} ^{\infty} \\ $$$$\mathrm{2}\left({I}_{\bigstar} +{I}\right)=\frac{\mathrm{1}}{−\mathrm{2}+{i}\mathrm{7}}−\frac{\mathrm{1}}{−\mathrm{2}+{i}}=\frac{−\mathrm{2}−{i}\mathrm{7}}{\mathrm{4}−\mathrm{49}}−\frac{−\mathrm{2}−{i}}{\mathrm{4}−\mathrm{1}} \\ $$$$\mathrm{2}\left({I}_{\bigstar} +{I}\right)=\frac{−\mathrm{2}}{−\mathrm{45}}+\frac{−{i}\mathrm{7}}{−\mathrm{45}}+\frac{\mathrm{2}+{i}}{\mathrm{3}} \\ $$$$\mathrm{2}\left({I}_{\bigstar} +{I}\right)=\frac{\mathrm{2}}{\mathrm{45}}+\frac{\mathrm{2}}{\mathrm{3}}+{i}\left(\frac{\mathrm{7}}{\mathrm{45}}+\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\mathrm{2}\left({I}_{\bigstar} +{I}\right)=\frac{\mathrm{2}+\mathrm{30}}{\mathrm{45}}+{i}\left(\frac{\mathrm{7}+\mathrm{15}}{\mathrm{45}}\right) \\ $$$${I}_{\bigstar} +{I}=\frac{\mathrm{16}}{\mathrm{45}}+{i}×\frac{\mathrm{11}}{\mathrm{45}} \\ $$$${I}=\frac{\mathrm{11}}{\mathrm{45}} \\ $$$${pls}\:{check}\:{is}\:{it}\:{correct} \\ $$

Commented by M±th+et£s last updated on 17/Apr/20

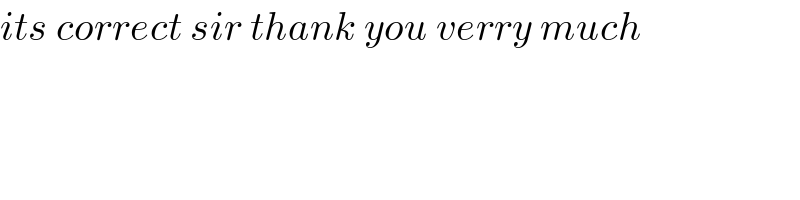
its correct sir thank you verry much

$${its}\:{correct}\:{sir}\:{thank}\:{you}\:{verry}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com