Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 89496 by I want to learn more last updated on 17/Apr/20

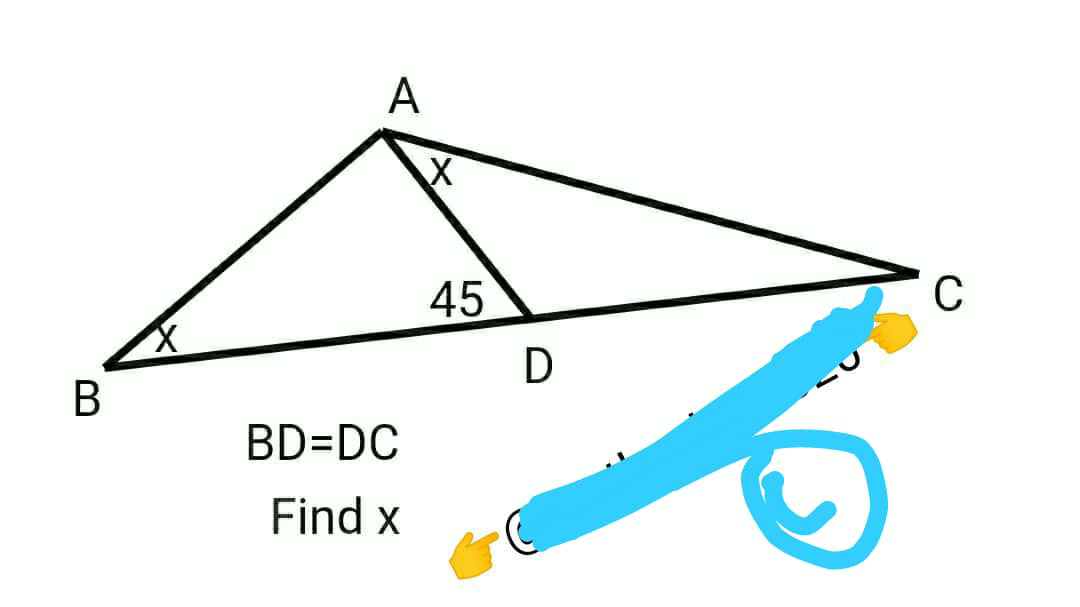
	Answered by me2love2math last updated on 17/Apr/20

	$u s e s i n e r u l e$
	Answered by $@ty@m123 last updated on 17/Apr/20
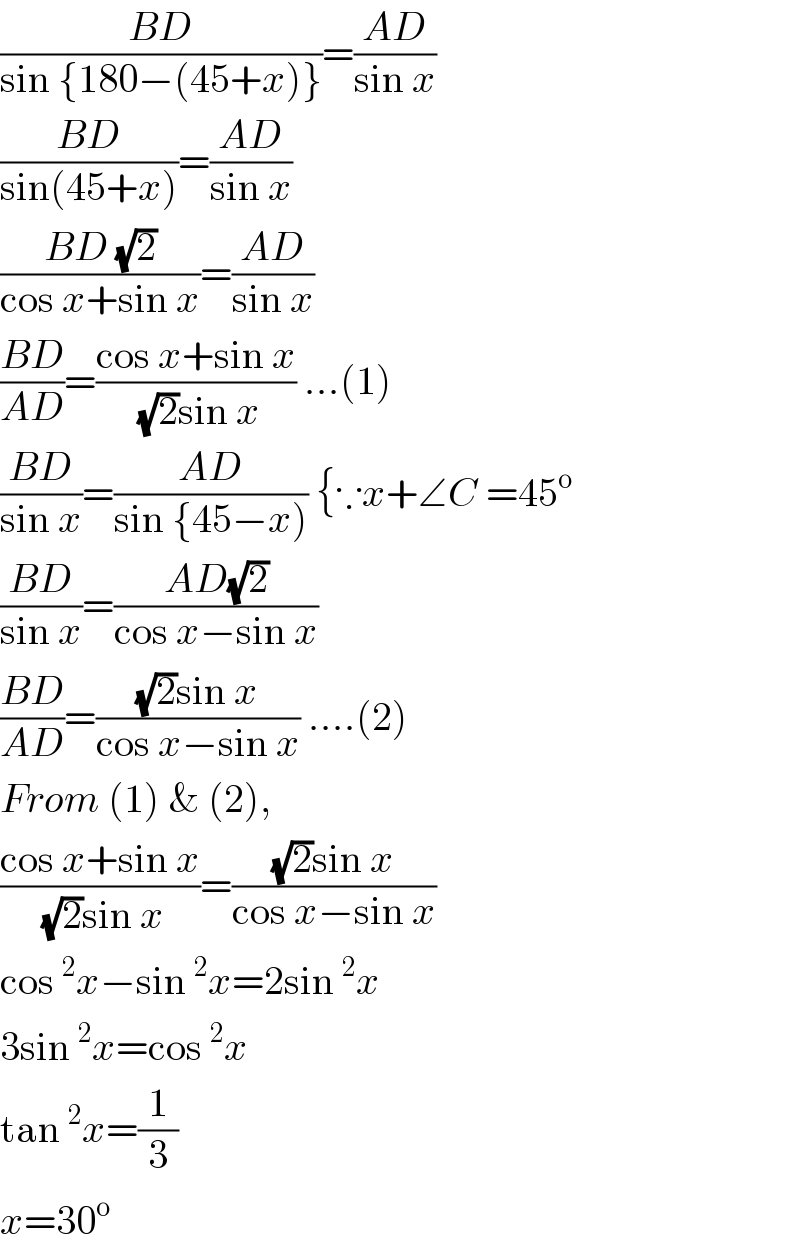
	$((BD)/(sin {180−(45+x)}))=((AD)/(sin x)) ((BD)/(sin(45+x)))=((AD)/(sin x)) ((BD (√2))/(cos x+sin x))=((AD)/(sin x)) ((BD)/(AD))=((cos x+sin x)/((√2)sin x)) ...(1) ((BD)/(sin x))=((AD)/(sin {45−x))) {∵x+∠C =45^o ((BD)/(sin x))=((AD(√2))/(cos x−sin x)) ((BD)/(AD))=(((√2)sin x)/(cos x−sin x)) ....(2) From (1) & (2), ((cos x+sin x)/((√2)sin x))=(((√2)sin x)/(cos x−sin x)) cos^2 x−sin^2 x=2sin^2 x 3sin^2 x=cos^2 x tan^2 x=(1/3) x=30^o$
	$\frac{B D}{\sin {180 - (45 + x)}} = \frac{A D}{\sin x}$ $\frac{B D}{\sin (45 + x)} = \frac{A D}{\sin x}$ $\frac{B D \sqrt{2}}{\cos x + \sin x} = \frac{A D}{\sin x}$ $\frac{B D}{A D} = \frac{\cos x + \sin x}{\sqrt{2} \sin x} . . . (1)$ $\frac{B D}{\sin x} = \frac{A D}{\sin {45 - x)} {∵ x + ∠ C = 45^{o}$ $\frac{B D}{\sin x} = \frac{A D \sqrt{2}}{\cos x - \sin x}$ $\frac{B D}{A D} = \frac{\sqrt{2} \sin x}{\cos x - \sin x} . . . . (2)$ $F r o m (1) & (2),$ $\frac{\cos x + \sin x}{\sqrt{2} \sin x} = \frac{\sqrt{2} \sin x}{\cos x - \sin x}$ $\cos^{2} x - \sin^{2} x = 2 \sin^{2} x$ $3 \sin^{2} x = \cos^{2} x$ $\tan^{2} x = \frac{1}{3}$ $x = 30^{o}$
	Commented by I want to learn more last updated on 17/Apr/20

	$Thanks sir .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum