
Question Number 89510 by Ar Brandon last updated on 17/Apr/20
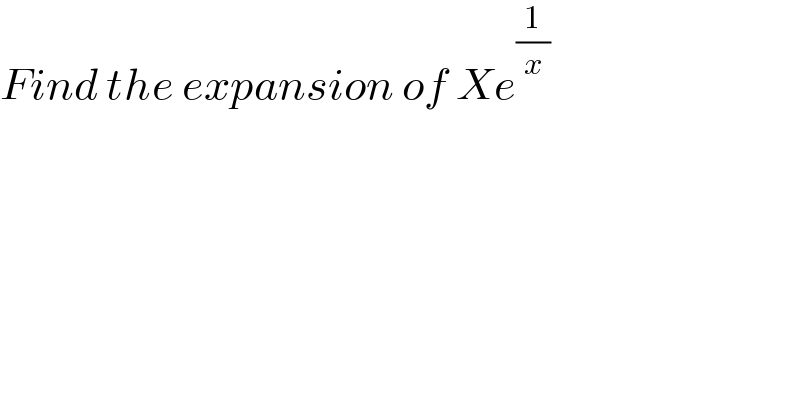
$${Find}\:{the}\:{expansion}\:{of}\:{Xe}^{\frac{\mathrm{1}}{{x}}} \: \\ $$
Commented by mathmax by abdo last updated on 18/Apr/20
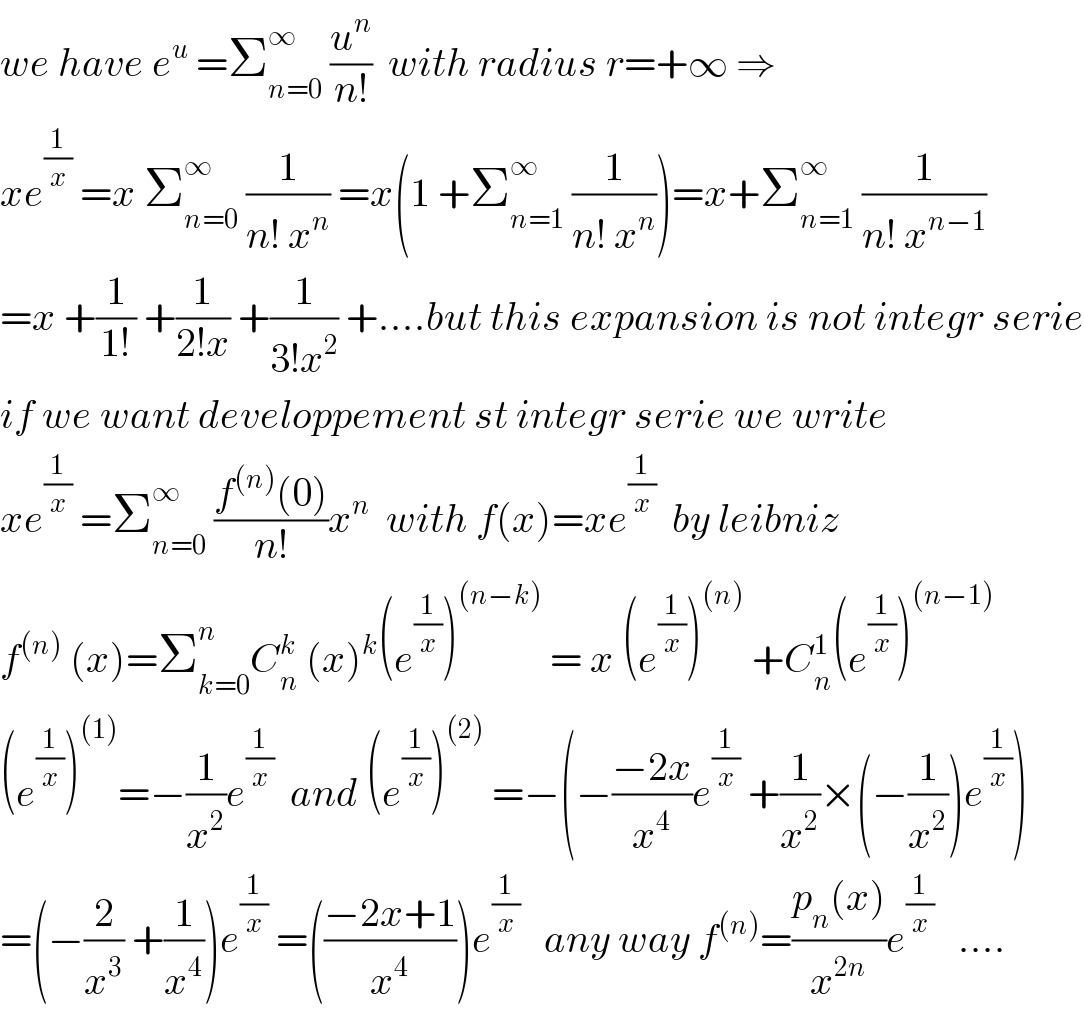
$${we}\:{have}\:{e}^{{u}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}} }{{n}!}\:\:{with}\:{radius}\:{r}=+\infty\:\Rightarrow \\ $$$${xe}^{\frac{\mathrm{1}}{{x}}} \:={x}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!\:{x}^{{n}} }\:={x}\left(\mathrm{1}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}!\:{x}^{{n}} }\right)={x}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}!\:{x}^{{n}−\mathrm{1}} } \\ $$$$={x}\:+\frac{\mathrm{1}}{\mathrm{1}!}\:+\frac{\mathrm{1}}{\mathrm{2}!{x}}\:+\frac{\mathrm{1}}{\mathrm{3}!{x}^{\mathrm{2}} }\:+....{but}\:{this}\:{expansion}\:{is}\:{not}\:{integr}\:{serie} \\ $$$${if}\:{we}\:{want}\:{developpement}\:{st}\:{integr}\:{serie}\:{we}\:{write} \\ $$$${xe}^{\frac{\mathrm{1}}{{x}}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}{x}^{{n}} \:\:{with}\:{f}\left({x}\right)={xe}^{\frac{\mathrm{1}}{{x}}} \:\:{by}\:{leibniz} \\ $$$${f}^{\left({n}\right)} \:\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} {C}_{{n}} ^{{k}} \:\left({x}\right)^{{k}} \left({e}^{\frac{\mathrm{1}}{{x}}} \right)^{\left({n}−{k}\right)} \:=\:{x}\:\left({e}^{\frac{\mathrm{1}}{{x}}} \right)^{\left({n}\right)} \:+{C}_{{n}} ^{\mathrm{1}} \left({e}^{\frac{\mathrm{1}}{{x}}} \right)^{\left({n}−\mathrm{1}\right)} \\ $$$$\left({e}^{\frac{\mathrm{1}}{{x}}} \right)^{\left(\mathrm{1}\right)} =−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{e}^{\frac{\mathrm{1}}{{x}}} \:\:{and}\:\left({e}^{\frac{\mathrm{1}}{{x}}} \right)^{\left(\mathrm{2}\right)} \:=−\left(−\frac{−\mathrm{2}{x}}{{x}^{\mathrm{4}} }{e}^{\frac{\mathrm{1}}{{x}}} \:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }×\left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){e}^{\frac{\mathrm{1}}{{x}}} \right) \\ $$$$=\left(−\frac{\mathrm{2}}{{x}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right){e}^{\frac{\mathrm{1}}{{x}}} \:=\left(\frac{−\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{4}} }\right){e}^{\frac{\mathrm{1}}{{x}}} \:\:\:{any}\:{way}\:{f}^{\left({n}\right)} =\frac{{p}_{{n}} \left({x}\right)}{{x}^{\mathrm{2}{n}} }{e}^{\frac{\mathrm{1}}{{x}}} \:\:\:.... \\ $$
Commented by Ar Brandon last updated on 18/Apr/20

$${Thank}\:{you}\: \\ $$
Commented by mathmax by abdo last updated on 18/Apr/20
$${you}\:{are}\:{welcome}\:. \\ $$
