Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 89593 by M±th+et£s last updated on 19/Apr/20

show that ∫_0 ^(π/2) ln(sec(x)) ln(csc(x)) dx=((π^2 ln^2 (2))/2)−(π^4 /(48))

$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sec}\left({x}\right)\right)\:{ln}\left({csc}\left({x}\right)\right)\:{dx}=\frac{\pi^{\mathrm{2}} \:{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\pi^{\mathrm{4}} }{\mathrm{48}} \\ $$

Commented by maths mind last updated on 19/Apr/20

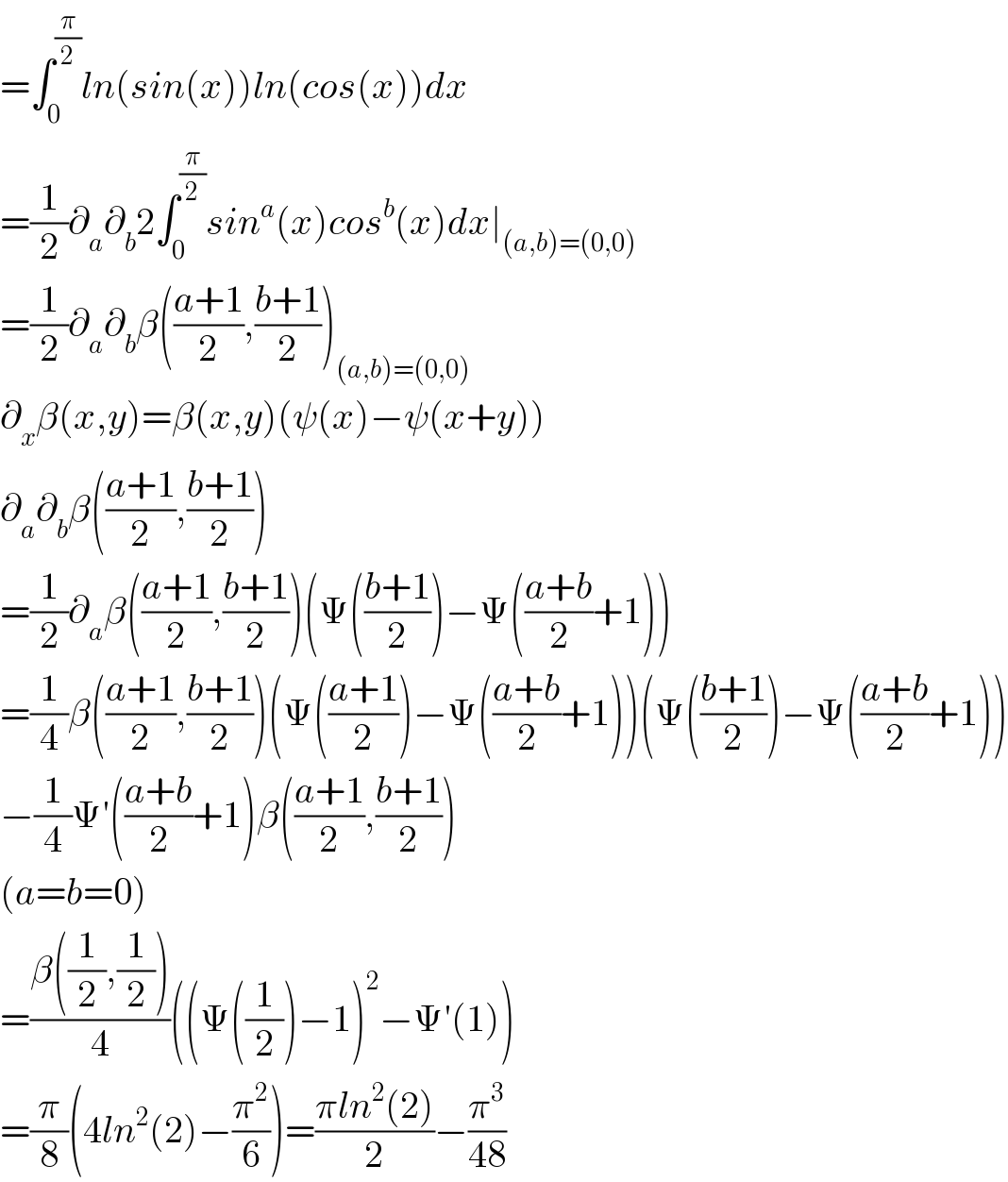
=∫_0 ^(π/2) ln(sin(x))ln(cos(x))dx =(1/2)∂_a ∂_b 2∫_0 ^(π/2) sin^a (x)cos^b (x)dx∣_((a,b)=(0,0)) =(1/2)∂_a ∂_b β(((a+1)/2),((b+1)/2))_((a,b)=(0,0)) ∂_x β(x,y)=β(x,y)(ψ(x)−ψ(x+y)) ∂_a ∂_b β(((a+1)/2),((b+1)/2)) =(1/2)∂_a β(((a+1)/2),((b+1)/2))(Ψ(((b+1)/2))−Ψ(((a+b)/2)+1)) =(1/4)β(((a+1)/2),((b+1)/2))(Ψ(((a+1)/2))−Ψ(((a+b)/2)+1))(Ψ(((b+1)/2))−Ψ(((a+b)/2)+1)) −(1/4)Ψ′(((a+b)/2)+1)β(((a+1)/2),((b+1)/2)) (a=b=0) =((β((1/2),(1/2)))/4)((Ψ((1/2))−1)^2 −Ψ′(1)) =(π/8)(4ln^2 (2)−(π^2 /6))=((πln^2 (2))/2)−(π^3 /(48))

$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){ln}\left({cos}\left({x}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\partial_{{a}} \partial_{{b}} \mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{{a}} \left({x}\right){cos}^{{b}} \left({x}\right){dx}\mid_{\left({a},{b}\right)=\left(\mathrm{0},\mathrm{0}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\partial_{{a}} \partial_{{b}} \beta\left(\frac{{a}+\mathrm{1}}{\mathrm{2}},\frac{{b}+\mathrm{1}}{\mathrm{2}}\right)_{\left({a},{b}\right)=\left(\mathrm{0},\mathrm{0}\right)} \\ $$$$\partial_{{x}} \beta\left({x},{y}\right)=\beta\left({x},{y}\right)\left(\psi\left({x}\right)−\psi\left({x}+{y}\right)\right) \\ $$$$\partial_{{a}} \partial_{{b}} \beta\left(\frac{{a}+\mathrm{1}}{\mathrm{2}},\frac{{b}+\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\partial_{{a}} \beta\left(\frac{{a}+\mathrm{1}}{\mathrm{2}},\frac{{b}+\mathrm{1}}{\mathrm{2}}\right)\left(\Psi\left(\frac{{b}+\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\frac{{a}+{b}}{\mathrm{2}}+\mathrm{1}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\beta\left(\frac{{a}+\mathrm{1}}{\mathrm{2}},\frac{{b}+\mathrm{1}}{\mathrm{2}}\right)\left(\Psi\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\frac{{a}+{b}}{\mathrm{2}}+\mathrm{1}\right)\right)\left(\Psi\left(\frac{{b}+\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\frac{{a}+{b}}{\mathrm{2}}+\mathrm{1}\right)\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{4}}\Psi'\left(\frac{{a}+{b}}{\mathrm{2}}+\mathrm{1}\right)\beta\left(\frac{{a}+\mathrm{1}}{\mathrm{2}},\frac{{b}+\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\left({a}={b}=\mathrm{0}\right) \\ $$$$=\frac{\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{4}}\left(\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}\right)^{\mathrm{2}} −\Psi'\left(\mathrm{1}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{8}}\left(\mathrm{4}{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\right)=\frac{\pi{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\pi^{\mathrm{3}} }{\mathrm{48}} \\ $$

Commented by M±th+et£s last updated on 19/Apr/20

thank you verry much its great solution

$${thank}\:{you}\:{verry}\:{much}\:{its}\:{great}\:{solution} \\ $$

Commented by maths mind last updated on 19/Apr/20

withe pleasur i lost my count mind is power!!

$${withe}\:\:{pleasur}\:{i}\:{lost}\:{my}\:{count} \\ $$$${mind}\:{is}\:{power}!! \\ $$$$ \\ $$

Commented by M±th+et£s last updated on 19/Apr/20

i am sorry this happened to you and i am verry happy to see you again in the forum

$${i}\:{am}\:{sorry}\:{this}\:{happened}\:{to}\:{you} \\ $$$${and}\:{i}\:{am}\:\:{verry}\:{happy}\:{to}\:{see}\:{you}\:{again} \\ $$$${in}\:{the}\:{forum} \\ $$

Commented by M±th+et£s last updated on 20/Apr/20

sir i can put all of your solutions on my questions here in this post if you want that?

$${sir}\:{i}\:{can}\:{put}\:{all}\:{of}\:{your}\:{solutions}\:{on}\:{my} \\ $$$${questions}\:{here}\:{in}\:{this}\:{post}\:{if}\:{you}\:{want} \\ $$$${that}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com