Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 89624 by M±th+et£s last updated on 18/Apr/20

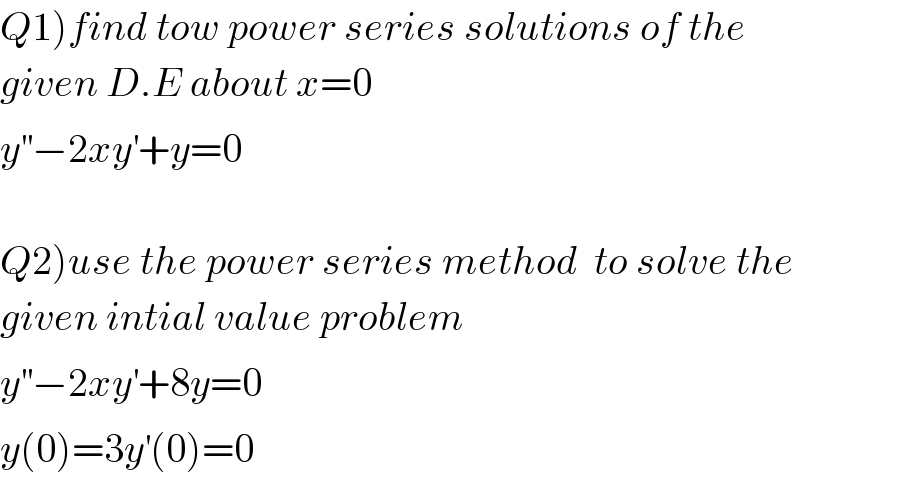
Q1)find tow power series solutions of the given D.E about x=0 y^(′′) −2xy^′ +y=0 Q2)use the power series method to solve the given intial value problem y^(′′) −2xy^′ +8y=0 y(0)=3y^′ (0)=0

$$\left.{Q}\mathrm{1}\right){find}\:{tow}\:{power}\:{series}\:{solutions}\:{of}\:{the}\: \\ $$$${given}\:{D}.{E}\:{about}\:{x}=\mathrm{0} \\ $$$${y}^{''} −\mathrm{2}{xy}^{'} +{y}=\mathrm{0} \\ $$$$ \\ $$$$\left.{Q}\mathrm{2}\right){use}\:{the}\:{power}\:{series}\:{method}\:\:{to}\:{solve}\:{the} \\ $$$${given}\:{intial}\:{value}\:{problem} \\ $$$${y}^{''} −\mathrm{2}{xy}^{'} +\mathrm{8}{y}=\mathrm{0} \\ $$$${y}\left(\mathrm{0}\right)=\mathrm{3}{y}^{'} \left(\mathrm{0}\right)=\mathrm{0} \\ $$

Commented by mathmax by abdo last updated on 18/Apr/20

y^(′′) −2xy^′ +y =0 let y =Σ_(n=0) ^∞ a_n x^n ⇒y^′ =Σ_(n=1) ^∞ na_n x^(n−1) =Σ_(n=0) ^∞ (n+1)a_(n+1) x^n and y^((2)) =Σ_(n=2) ^∞ n(n−1)a_n x^(n−2) =Σ_(n=0) ^∞ (n+2)(n+1)a_(n+2) x^n (e)⇒Σ_(n=0) ^∞ (n+2)(n+1)a_(n+2) x^n −2Σ_(n=0) ^∞ (n+1)a_(n+1) x^(n+1) +Σ_(n=0) ^∞ a_n x^n =0 ⇒ Σ_(n=0) ^∞ (n+1)(n+2)a_(n+2) x^n −2Σ_(n=1) ^∞ na_n x^n +Σ_(n=0) ^∞ a_n x^n =0 ⇒2a_2 +Σ_(n=1) ^∞ {(n+1)(n+2)a_(n+2) +(1−2n)a_n }x^n =0 ⇒ { ((a_2 =0)),(((n+1)(n+2)a_(n+2) =(2n−1)a_n ∀n≥1 ⇒)) :} { ((a_2 =0)),((a_(n+2) =((2n−1)/((n+1)(n+2)))a_n ∀n≥1)) :} a_(2n+2) =((4n−1)/((2n+1)(2n+2)))a_(2n) ⇒Π_(k=2) ^n (a_(2k+2) /a_(2k) ) =Π_(k=2) ^n ((4k−1)/(2(2k+1)(k+1))) (a_6 /a_4 )......(a_(2n) /a_(2n−2) ).(a_(2n+2) /a_(2n) ) =(1/2^n )Π_(k=1) ^n ((4k−1)/((k+1)(2k+1))) ⇒ a_(2n+2) =(a_4 /2^n )((3/(2.3))×(7/(3.5))×((11)/(4×7))×.....((4n−1)/((n+1)(2n+1)))) we follow the same way to find a_(2n+1) ...

$${y}^{''} −\mathrm{2}{xy}^{'} \:+{y}\:=\mathrm{0}\:\:{let}\:{y}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{a}_{{n}} {x}^{{n}} \:\:\Rightarrow{y}^{'} =\sum_{{n}=\mathrm{1}} ^{\infty} {na}_{{n}} {x}^{{n}−\mathrm{1}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \left({n}+\mathrm{1}\right){a}_{{n}+\mathrm{1}} {x}^{{n}} \\ $$$${and}\:{y}^{\left(\mathrm{2}\right)} =\sum_{{n}=\mathrm{2}} ^{\infty} {n}\left({n}−\mathrm{1}\right){a}_{{n}} {x}^{{n}−\mathrm{2}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right){a}_{{n}+\mathrm{2}} {x}^{{n}} \\ $$$$\left({e}\right)\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right){a}_{{n}+\mathrm{2}} {x}^{{n}} \:−\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \left({n}+\mathrm{1}\right){a}_{{n}+\mathrm{1}} {x}^{{n}+\mathrm{1}} \\ $$$$+\sum_{{n}=\mathrm{0}} ^{\infty} {a}_{{n}} {x}^{{n}} =\mathrm{0}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right){a}_{{n}+\mathrm{2}} {x}^{{n}} \:−\mathrm{2}\sum_{{n}=\mathrm{1}} ^{\infty} {na}_{{n}} {x}^{{n}} \:+\sum_{{n}=\mathrm{0}} ^{\infty} {a}_{{n}} {x}^{{n}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{a}_{\mathrm{2}} \:+\sum_{{n}=\mathrm{1}} ^{\infty} \left\{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right){a}_{{n}+\mathrm{2}} +\left(\mathrm{1}−\mathrm{2}{n}\right){a}_{{n}} \right\}{x}^{{n}} =\mathrm{0}\:\Rightarrow \\ $$$$\begin{cases}{{a}_{\mathrm{2}} \:=\mathrm{0}}\\{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right){a}_{{n}+\mathrm{2}} =\left(\mathrm{2}{n}−\mathrm{1}\right){a}_{{n}} \:\:\forall{n}\geqslant\mathrm{1}\:\Rightarrow}\end{cases} \\ $$$$\begin{cases}{{a}_{\mathrm{2}} =\mathrm{0}}\\{{a}_{{n}+\mathrm{2}} =\frac{\mathrm{2}{n}−\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{a}_{{n}} \:\:\forall{n}\geqslant\mathrm{1}}\end{cases} \\ $$$${a}_{\mathrm{2}{n}+\mathrm{2}} =\frac{\mathrm{4}{n}−\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{2}\right)}{a}_{\mathrm{2}{n}} \:\Rightarrow\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{{a}_{\mathrm{2}{k}+\mathrm{2}} }{{a}_{\mathrm{2}{k}} }\:=\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{4}{k}−\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)\left({k}+\mathrm{1}\right)} \\ $$$$\frac{{a}_{\mathrm{6}} }{{a}_{\mathrm{4}} }......\frac{{a}_{\mathrm{2}{n}} }{{a}_{\mathrm{2}{n}−\mathrm{2}} }.\frac{{a}_{\mathrm{2}{n}+\mathrm{2}} }{{a}_{\mathrm{2}{n}} }\:=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\prod_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{4}{k}−\mathrm{1}}{\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}\:\Rightarrow \\ $$$${a}_{\mathrm{2}{n}+\mathrm{2}} =\frac{{a}_{\mathrm{4}} }{\mathrm{2}^{{n}} }\left(\frac{\mathrm{3}}{\mathrm{2}.\mathrm{3}}×\frac{\mathrm{7}}{\mathrm{3}.\mathrm{5}}×\frac{\mathrm{11}}{\mathrm{4}×\mathrm{7}}×.....\frac{\mathrm{4}{n}−\mathrm{1}}{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}\right) \\ $$$${we}\:{follow}\:{the}\:{same}\:{way}\:{to}\:{find}\:\:{a}_{\mathrm{2}{n}+\mathrm{1}} ... \\ $$

Commented by M±th+et£s last updated on 18/Apr/20

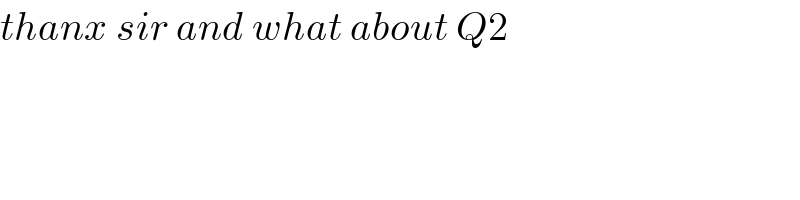
thanx sir and what about Q2

$${thanx}\:{sir}\:{and}\:{what}\:{about}\:{Q}\mathrm{2} \\ $$

Commented by mathmax by abdo last updated on 18/Apr/20

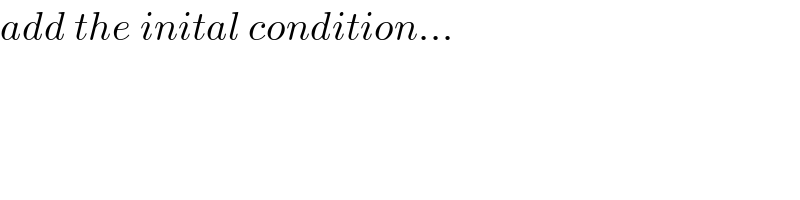
add the inital condition...

$${add}\:{the}\:{inital}\:{condition}... \\ $$

Answered by ajfour last updated on 18/Apr/20

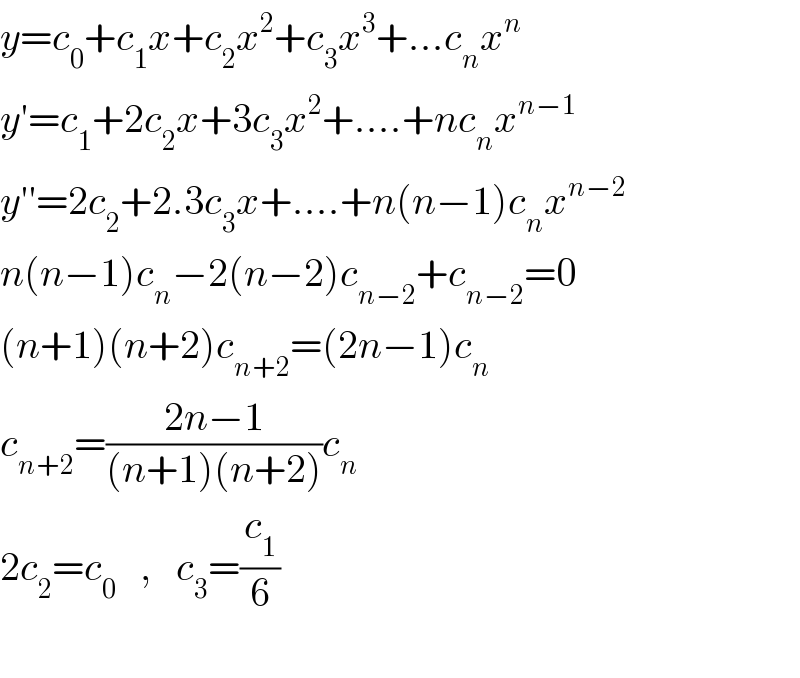
y=c_0 +c_1 x+c_2 x^2 +c_3 x^3 +...c_n x^n y′=c_1 +2c_2 x+3c_3 x^2 +....+nc_n x^(n−1) y′′=2c_2 +2.3c_3 x+....+n(n−1)c_n x^(n−2) n(n−1)c_n −2(n−2)c_(n−2) +c_(n−2) =0 (n+1)(n+2)c_(n+2) =(2n−1)c_n c_(n+2) =((2n−1)/((n+1)(n+2)))c_n 2c_2 =c_0 , c_3 =(c_1 /6)

$${y}={c}_{\mathrm{0}} +{c}_{\mathrm{1}} {x}+{c}_{\mathrm{2}} {x}^{\mathrm{2}} +{c}_{\mathrm{3}} {x}^{\mathrm{3}} +...{c}_{{n}} {x}^{{n}} \\ $$$${y}'={c}_{\mathrm{1}} +\mathrm{2}{c}_{\mathrm{2}} {x}+\mathrm{3}{c}_{\mathrm{3}} {x}^{\mathrm{2}} +....+{nc}_{{n}} {x}^{{n}−\mathrm{1}} \\ $$$${y}''=\mathrm{2}{c}_{\mathrm{2}} +\mathrm{2}.\mathrm{3}{c}_{\mathrm{3}} {x}+....+{n}\left({n}−\mathrm{1}\right){c}_{{n}} {x}^{{n}−\mathrm{2}} \\ $$$${n}\left({n}−\mathrm{1}\right){c}_{{n}} −\mathrm{2}\left({n}−\mathrm{2}\right){c}_{{n}−\mathrm{2}} +{c}_{{n}−\mathrm{2}} =\mathrm{0} \\ $$$$\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right){c}_{{n}+\mathrm{2}} =\left(\mathrm{2}{n}−\mathrm{1}\right){c}_{{n}} \\ $$$${c}_{{n}+\mathrm{2}} =\frac{\mathrm{2}{n}−\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{c}_{{n}} \\ $$$$\mathrm{2}{c}_{\mathrm{2}} ={c}_{\mathrm{0}} \:\:\:,\:\:\:{c}_{\mathrm{3}} =\frac{{c}_{\mathrm{1}} }{\mathrm{6}} \\ $$$$ \\ $$

Commented by M±th+et£s last updated on 18/Apr/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Commented by M±th+et£s last updated on 18/Apr/20

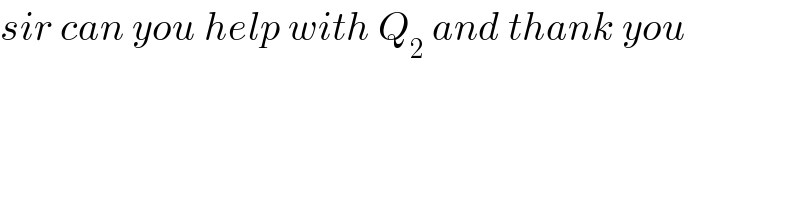
sir can you help with Q_2 and thank you

$${sir}\:{can}\:{you}\:{help}\:{with}\:{Q}_{\mathrm{2}} \:{and}\:{thank}\:{you} \\ $$

Commented by ajfour last updated on 18/Apr/20

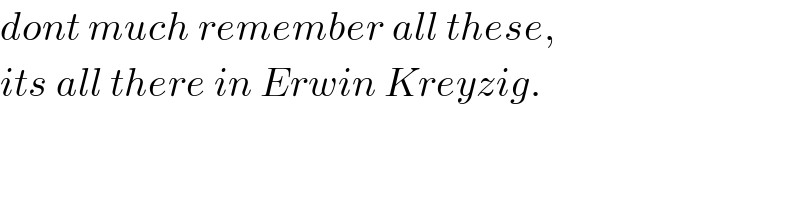
dont much remember all these, its all there in Erwin Kreyzig.

$${dont}\:{much}\:{remember}\:{all}\:{these}, \\ $$$${its}\:{all}\:{there}\:{in}\:{Erwin}\:{Kreyzig}. \\ $$

Commented by M±th+et£s last updated on 18/Apr/20

ok sir thank you

$${ok}\:{sir}\:{thank}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com