
Question Number 89753 by jagoll last updated on 19/Apr/20
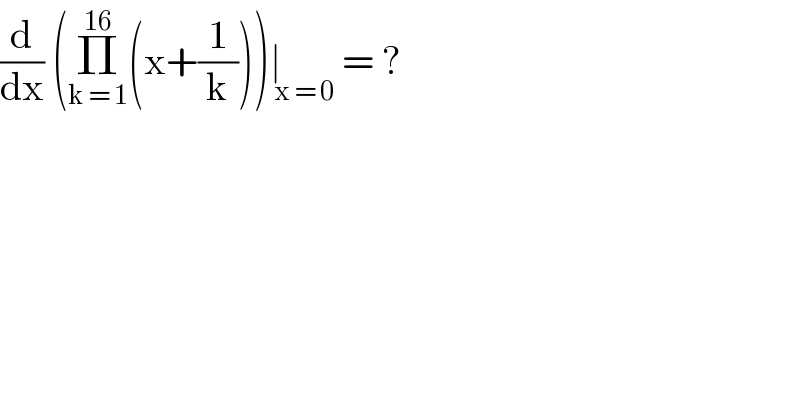
$$\frac{\mathrm{d}}{\mathrm{dx}}\:\left(\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{\mathrm{16}} {\prod}}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{k}}\right)\right)\underset{\:\mathrm{x}\:=\:\mathrm{0}} {\mid}\:=\:? \\ $$
Commented by mr W last updated on 19/Apr/20
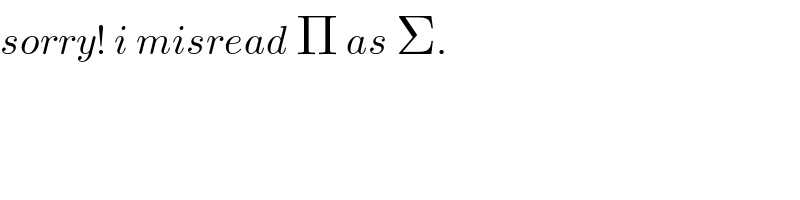
$${sorry}!\:{i}\:{misread}\:\Pi\:{as}\:\Sigma. \\ $$
Commented by john santu last updated on 19/Apr/20

$${thank}\:{you}\:{sir} \\ $$$$ \\ $$
Commented by john santu last updated on 19/Apr/20
![(d/dx) [ (x+1)(x+(1/2))(x+(1/3))...(x+(1/(16)))] = (x+(1/2))(x+(1/3))...+(x+(1/(16))) + (x+1)(x+(1/3))...(x+(1/(16)))+... = Σ_(k = 1 ) ^(16) ((Π_(n = 1) ^(16) (x+(1/n)))/(x+(1/k) )) ∣_(x = 0) = ((Σ_(n = 1) ^(16) ((1/n)))/(1/k)) = (1/(16!)) ×((16(16+1))/2) = (1/(15!)) ×((17)/2)](Q89759.png)
$$\frac{{d}}{{dx}}\:\left[\:\left({x}+\mathrm{1}\right)\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{1}}{\mathrm{3}}\right)...\left({x}+\frac{\mathrm{1}}{\mathrm{16}}\right)\right] \\ $$$$=\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{1}}{\mathrm{3}}\right)...+\left({x}+\frac{\mathrm{1}}{\mathrm{16}}\right)\:+ \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+\frac{\mathrm{1}}{\mathrm{3}}\right)...\left({x}+\frac{\mathrm{1}}{\mathrm{16}}\right)+... \\ $$$$=\:\underset{{k}\:=\:\mathrm{1}\:} {\overset{\mathrm{16}} {\sum}}\frac{\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{16}} {\prod}}\left({x}+\frac{\mathrm{1}}{{n}}\right)}{{x}+\frac{\mathrm{1}}{{k}}\:}\:\mid_{{x}\:=\:\mathrm{0}} \\ $$$$=\:\frac{\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{16}} {\sum}}\:\left(\frac{\mathrm{1}}{{n}}\right)}{\frac{\mathrm{1}}{{k}}}\:=\:\frac{\mathrm{1}}{\mathrm{16}!}\:×\frac{\mathrm{16}\left(\mathrm{16}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{15}!}\:×\frac{\mathrm{17}}{\mathrm{2}} \\ $$
Commented by john santu last updated on 19/Apr/20
![tes for Π_(k = 1) ^3 (x+(1/k)) = (x+1)(x+(1/2))(x+(1/3)) = (x+1)(((2x+1)/2))(((3x+1)/3)) = (1/6)(x+1)(6x^2 +5x+1) = (1/6)(6x^3 +11x^2 +6x+1) (d/dx) [(1/6)(6x^3 +11x^2 +6x+1)] = (1/6)(18x^2 +22x+6) ∣_(x = 0 ) = (6/6) = 1](Q89760.png)
$${tes}\:{for}\:\underset{{k}\:=\:\mathrm{1}} {\overset{\mathrm{3}} {\prod}}\left({x}+\frac{\mathrm{1}}{{k}}\right)\:= \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{1}}{\mathrm{3}}\right)\:= \\ $$$$\left({x}+\mathrm{1}\right)\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{3}{x}+\mathrm{1}}{\mathrm{3}}\right)\:=\: \\ $$$$\frac{\mathrm{1}}{\mathrm{6}}\left({x}+\mathrm{1}\right)\left(\mathrm{6}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{1}\right)\:=\: \\ $$$$\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{6}{x}^{\mathrm{3}} +\mathrm{11}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{1}\right)\: \\ $$$$\frac{{d}}{{dx}}\:\left[\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{6}{x}^{\mathrm{3}} +\mathrm{11}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{1}\right)\right]\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{18}{x}^{\mathrm{2}} +\mathrm{22}{x}+\mathrm{6}\right)\:\mid_{{x}\:=\:\mathrm{0}\:} \\ $$$$=\:\frac{\mathrm{6}}{\mathrm{6}}\:=\:\mathrm{1}\: \\ $$$$ \\ $$
Commented by john santu last updated on 19/Apr/20
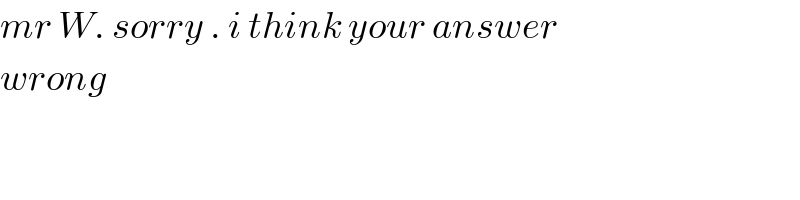
$${mr}\:{W}.\:{sorry}\:.\:{i}\:{think}\:{your}\:{answer} \\ $$$${wrong}\: \\ $$
Commented by john santu last updated on 19/Apr/20
![in generally (d/dx)[Π_(k = 1) ^n (x+(1/k))] ∣_(x = 0 ) = (((n+1))/(2(n−1)!))](Q89763.png)
$${in}\:{generally}\: \\ $$$$\frac{{d}}{{dx}}\left[\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\prod}}\:\left({x}+\frac{\mathrm{1}}{{k}}\right)\right]\:\mid_{{x}\:=\:\mathrm{0}\:} \:=\:\frac{\left({n}+\mathrm{1}\right)}{\mathrm{2}\left({n}−\mathrm{1}\right)!}\: \\ $$
Answered by mr W last updated on 19/Apr/20
![y=Π_(k = 1) ^n (x+(1/k)) ln y=Σ_(k = 1) ^n [ln (x+(1/k))] (1/y)(dy/dx)=Σ_(k = 1) ^n [(d/dx)ln (x+(1/k))] (1/y)(dy/dx)=Σ_(k = 1) ^n (1/(x+(1/k))) ⇒(dy/dx)=Π_(k = 1) ^n (x+(1/k))Σ_(k = 1) ^n ((1/(x+(1/k)))) at x=0: (dy/dx)=Π_(k = 1) ^n ((1/k))Σ_(k = 1) ^n ((1/(1/k)))=Π_(k = 1) ^n (1/k)Σ_(k = 1) ^n k =(1/(n!))×((n(n+1))/2) =((n+1)/(2(n−1)!)) with n=16: (dy/dx)∣_(x=0) =((17)/(2×15!))](Q89769.png)
$${y}=\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{k}}\right) \\ $$$$\mathrm{ln}\:{y}=\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\left[\mathrm{ln}\:\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{k}}\right)\right] \\ $$$$\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dx}}=\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\left[\frac{{d}}{{dx}}\mathrm{ln}\:\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{k}}\right)\right] \\ $$$$\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dx}}=\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{k}}} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{k}}\right)\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{k}}}\right) \\ $$$${at}\:{x}=\mathrm{0}: \\ $$$$\frac{{dy}}{{dx}}=\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{{n}} {\prod}}\left(\frac{\mathrm{1}}{\mathrm{k}}\right)\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\frac{\mathrm{1}}{{k}}}\right)=\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{{n}} {\prod}}\frac{\mathrm{1}}{\mathrm{k}}\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}{k} \\ $$$$=\frac{\mathrm{1}}{{n}!}×\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\frac{{n}+\mathrm{1}}{\mathrm{2}\left({n}−\mathrm{1}\right)!} \\ $$$${with}\:{n}=\mathrm{16}: \\ $$$$\frac{{dy}}{{dx}}\mid_{{x}=\mathrm{0}} =\frac{\mathrm{17}}{\mathrm{2}×\mathrm{15}!} \\ $$
Commented by john santu last updated on 19/Apr/20

$${great}\:{sir}\: \\ $$
Commented by jagoll last updated on 19/Apr/20
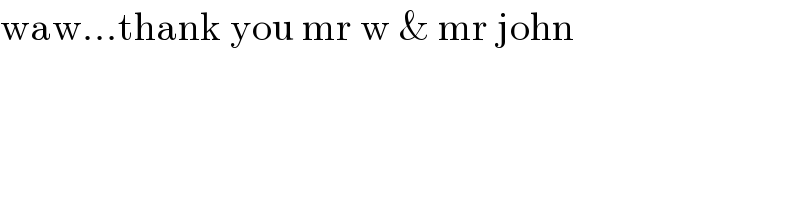
$$\mathrm{waw}...\mathrm{thank}\:\mathrm{you}\:\mathrm{mr}\:\mathrm{w}\:\&\:\mathrm{mr}\:\mathrm{john} \\ $$
