Question Number 89846 by M±th+et£s last updated on 19/Apr/20
$$\int_{−\mathrm{1}} ^{\mathrm{1}} \:{x}\:{cosh}\left({x}\right)\:{ln}\left(\mathrm{1}+{e}^{{x}} \right)\:{dx} \\ $$
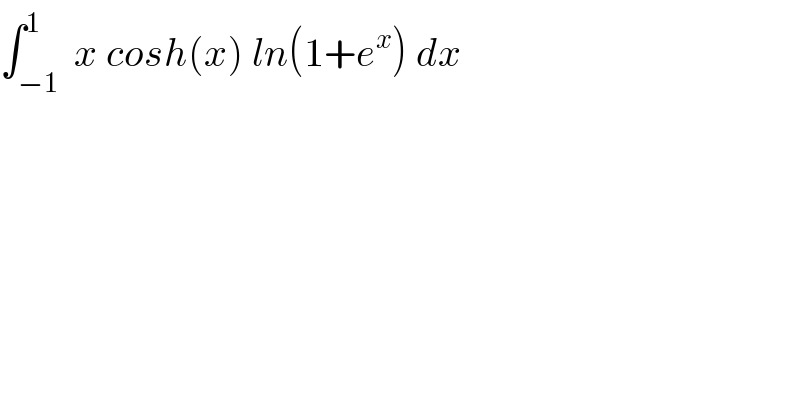
Commented by M±th+et£s last updated on 19/Apr/20
$${thank}\:{you}\:{verry}\:{much} \\ $$
Commented by abdomathmax last updated on 19/Apr/20
![I =∫_(−1) ^1 x((e^x +e^(−x) )/2)ln(1+e^x )dt =(1/2)∫_(−1) ^1 xe^x ln(1+e^x )dx+(1/2)∫_(−1) ^1 x e^(−x) ln(1+e^x )dx =H +K H =∫_(−1) ^1 xe^x ln(1+e^x )dx by parts u^′ =xe^x and v=ln(1+e^x ) ⇒u =∫xe^x =xe^x −∫e^x =(x−1)e^x H =[(x−1)e^x ln(1+e^x )]_(−1) ^1 −∫_(−1) ^1 (x−1)e^x ×(e^x /(1+e^x ))dx =2 e^(−1) ln(1+e^(−1) )−∫_(−1) ^1 (((x−1)e^(2x) )/(1+e^x )) dx ∫_(−1) ^1 (((x−1)e^(2x) )/(1+e^x ))dx =_(e^x =t) ∫_e^(−1) ^e (((lnt−1)t^2 )/(1+t))×(dt/t) =∫_e^(−1) ^e ((tlnt−t)/(1+t))dt =[ln(t)ln(t)]_e^(−1) ^e −∫_e^(−1) ^e lnt ln(1+t)dt =2 −∫_e^(−1) ^e ln(t)ln(1+t)dt we have ∫_e^(−1) ^e ln(t)ln(1+t)dt =∫_e^(−1) ^1 ln(t)ln(1+t)dt + ∫_1 ^e ln(t)ln(1+t)dt ln^′ (1+t) =Σ_(n=0) ^∞ (−1)^n t^n ⇒ ln(1+t) =Σ_(n=0) ^∞ (((−1)^n )/(n+1))t^(n+1) +c (c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) t^n )/n) ⇒ ∫_e^(−1) ^1 ln(t)ln(1+t)dt =∫_e^(−1) ^1 lnt(Σ_(n=1) ^∞ (((−1)^(n−1) )/n)t^n )dt =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_e^(−1) ^1 t^n ln(t)dt A_n =∫_e^(−1) ^1 t^n ln(t)dt =[(t^(n+1) /(n+1))ln(t)]_e^(−1) ^1 −∫_e^(−1) ^1 (t^n /(n+1))dt =(1/(n+1))e^(−n−1) −(1/(n+1))[(1/(n+1))t^(n+1) ]_e^(−1) ^1 ...be continued...](Q89854.png)
$${I}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \:{x}\frac{{e}^{{x}} \:+{e}^{−{x}} }{\mathrm{2}}{ln}\left(\mathrm{1}+{e}^{{x}} \right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{1}} \:{xe}^{{x}} {ln}\left(\mathrm{1}+{e}^{{x}} \right){dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{1}} \:{x}\:{e}^{−{x}} {ln}\left(\mathrm{1}+{e}^{{x}} \right){dx} \\ $$$$={H}\:+{K} \\ $$$${H}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \:{xe}^{{x}} {ln}\left(\mathrm{1}+{e}^{{x}} \right){dx}\:{by}\:{parts}\:{u}^{'} ={xe}^{{x}} \:{and} \\ $$$${v}={ln}\left(\mathrm{1}+{e}^{{x}} \right)\:\Rightarrow{u}\:=\int{xe}^{{x}} \:={xe}^{{x}} −\int{e}^{{x}} \:=\left({x}−\mathrm{1}\right){e}^{{x}} \\ $$$${H}\:=\left[\left({x}−\mathrm{1}\right){e}^{{x}} {ln}\left(\mathrm{1}+{e}^{{x}} \right)\right]_{−\mathrm{1}} ^{\mathrm{1}} −\int_{−\mathrm{1}} ^{\mathrm{1}} \left({x}−\mathrm{1}\right){e}^{{x}} ×\frac{{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }{dx} \\ $$$$=\mathrm{2}\:{e}^{−\mathrm{1}} {ln}\left(\mathrm{1}+{e}^{−\mathrm{1}} \right)−\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{\left({x}−\mathrm{1}\right){e}^{\mathrm{2}{x}} }{\mathrm{1}+{e}^{{x}} }\:{dx} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{\left({x}−\mathrm{1}\right){e}^{\mathrm{2}{x}} }{\mathrm{1}+{e}^{{x}} }{dx}\:=_{{e}^{{x}} ={t}} \:\:\:\int_{{e}^{−\mathrm{1}} } ^{{e}} \:\frac{\left({lnt}−\mathrm{1}\right){t}^{\mathrm{2}} }{\mathrm{1}+{t}}×\frac{{dt}}{{t}} \\ $$$$=\int_{{e}^{−\mathrm{1}} } ^{{e}} \:\frac{{tlnt}−{t}}{\mathrm{1}+{t}}{dt}\:=\left[{ln}\left({t}\right){ln}\left({t}\right)\right]_{{e}^{−\mathrm{1}} } ^{{e}} −\int_{{e}^{−\mathrm{1}} } ^{{e}} {lnt}\:{ln}\left(\mathrm{1}+{t}\right){dt} \\ $$$$=\mathrm{2}\:−\int_{{e}^{−\mathrm{1}} } ^{{e}} \:{ln}\left({t}\right){ln}\left(\mathrm{1}+{t}\right){dt}\:\:{we}\:{have} \\ $$$$\int_{{e}^{−\mathrm{1}} } ^{{e}} {ln}\left({t}\right){ln}\left(\mathrm{1}+{t}\right){dt}\:=\int_{{e}^{−\mathrm{1}} } ^{\mathrm{1}} \:{ln}\left({t}\right){ln}\left(\mathrm{1}+{t}\right){dt}\:+ \\ $$$$\int_{\mathrm{1}} ^{{e}} \:{ln}\left({t}\right){ln}\left(\mathrm{1}+{t}\right){dt} \\ $$$${ln}^{'} \left(\mathrm{1}+{t}\right)\:\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {t}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{t}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{t}^{{n}+\mathrm{1}} \:+{c}\:\:\left({c}=\mathrm{0}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {t}^{{n}} }{{n}}\:\Rightarrow \\ $$$$\int_{{e}^{−\mathrm{1}} } ^{\mathrm{1}} {ln}\left({t}\right){ln}\left(\mathrm{1}+{t}\right){dt}\:=\int_{{e}^{−\mathrm{1}} } ^{\mathrm{1}} {lnt}\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{t}^{{n}} \right){dt} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{{e}^{−\mathrm{1}} } ^{\mathrm{1}} \:{t}^{{n}} \:{ln}\left({t}\right){dt}\: \\ $$$${A}_{{n}} =\int_{{e}^{−\mathrm{1}} } ^{\mathrm{1}} \:{t}^{{n}} \:{ln}\left({t}\right){dt}\:=\left[\frac{{t}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{ln}\left({t}\right)\right]_{{e}^{−\mathrm{1}} } ^{\mathrm{1}} −\int_{{e}^{−\mathrm{1}} } ^{\mathrm{1}} \frac{{t}^{{n}} }{{n}+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}{e}^{−{n}−\mathrm{1}} −\frac{\mathrm{1}}{{n}+\mathrm{1}}\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{t}^{{n}+\mathrm{1}} \right]_{{e}^{−\mathrm{1}} } ^{\mathrm{1}} \\ $$$$...{be}\:{continued}... \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 19/Apr/20
$${you}\:{are}\:{welcome}. \\ $$
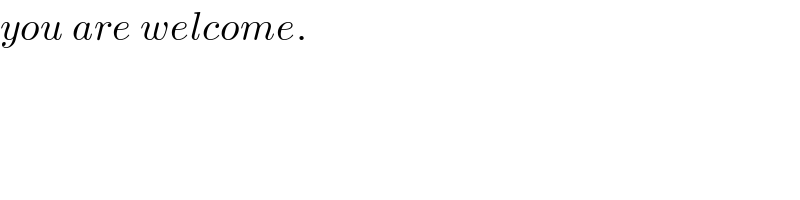
Answered by M±th+et£s last updated on 19/Apr/20
$$\int_{−\mathrm{1}} ^{\mathrm{1}} {x}\:{cosh}\left({x}\right)\:{ln}\left(\mathrm{1}+{e}^{{x}} \right).......\left(\mathrm{1}\right) \\ $$$${let}\:{y}=−{x}\:\Rightarrow\:{dy}=−{dx} \\ $$$${I}=\int_{−\mathrm{1}} ^{\mathrm{1}} −{y}\:{cosh}\left(−{y}\right)\:{ln}\left(\mathrm{1}+{e}^{{y}} \right)\:{dx} \\ $$$${I}=\int_{−\mathrm{1}} ^{\mathrm{1}} −{y}\:{cosh}\left(−{y}\right)\:{ln}\left(\frac{\mathrm{1}+{e}^{{y}} }{{e}^{{y}} }\right)\:{dy} \\ $$$${I}=\int_{−\mathrm{1}} ^{\mathrm{1}} −{y}\:{cosh}\left({y}\right)\:{ln}\left(\mathrm{1}+{e}^{{y}} \right)\:+\:{y}\:{cosh}\left({y}\right)\:{ln}\left({e}^{{y}} \right)\:{dy} \\ $$$${I}=\int_{−\mathrm{1}} ^{\mathrm{1}} −{y}\:{cosh}\left({y}\right)\:{ln}\left(\mathrm{1}+{e}^{{y}} \right)+{y}^{\mathrm{2}} \:{cosh}\left({y}\right)\:{dy}....\left(\mathrm{2}\right) \\ $$$${add}\left(\mathrm{1}\right)\:{to}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{2}{I}=\int_{−\mathrm{1}} ^{\mathrm{1}} {x}^{\mathrm{2}} {cosh}\left({x}\right)\:{dx} \\ $$$${integrate}\:{by}\:{parts} \\ $$$$\mathrm{2}{I}=\left({x}^{\mathrm{2}} +\mathrm{2}\right){sinh}\left({x}\right)−\mathrm{2}{x}\:{cosh}\left({x}\right)\mid_{−\mathrm{1}} ^{\mathrm{1}} \:._{} ^{} \\ $$$$\mathrm{2}{I}=\mathrm{6}{sinh}\left(\mathrm{1}\right)−\mathrm{4}{cosh}\left(\mathrm{1}\right) \\ $$$${I}=\mathrm{3}{sinh}\left(\mathrm{1}\right)−\mathrm{2}{cosh}\left(\mathrm{1}\right) \\ $$