Question and Answers Forum
Question Number 89849 by ajfour last updated on 19/Apr/20
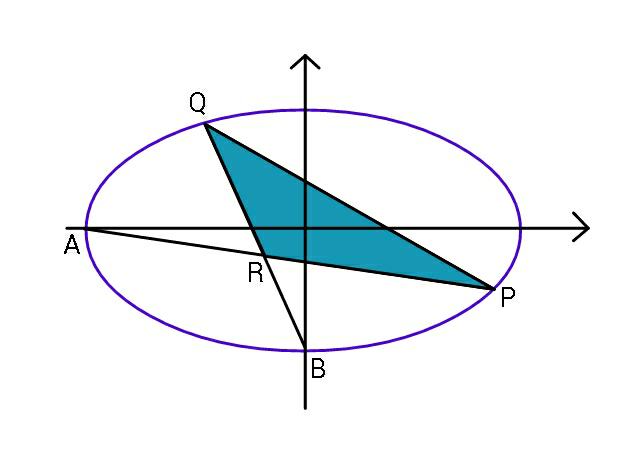
Commented by ajfour last updated on 19/Apr/20

Answered by mr W last updated on 19/Apr/20
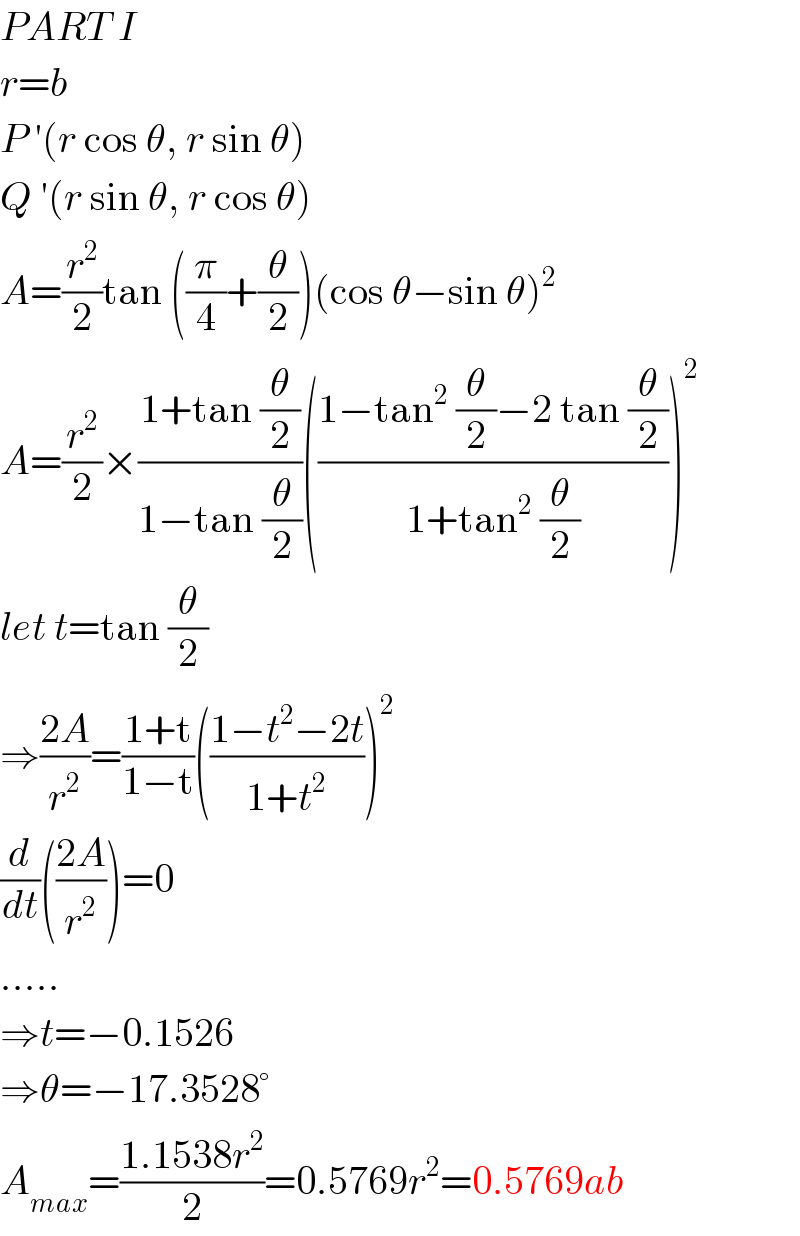
Commented by mr W last updated on 19/Apr/20
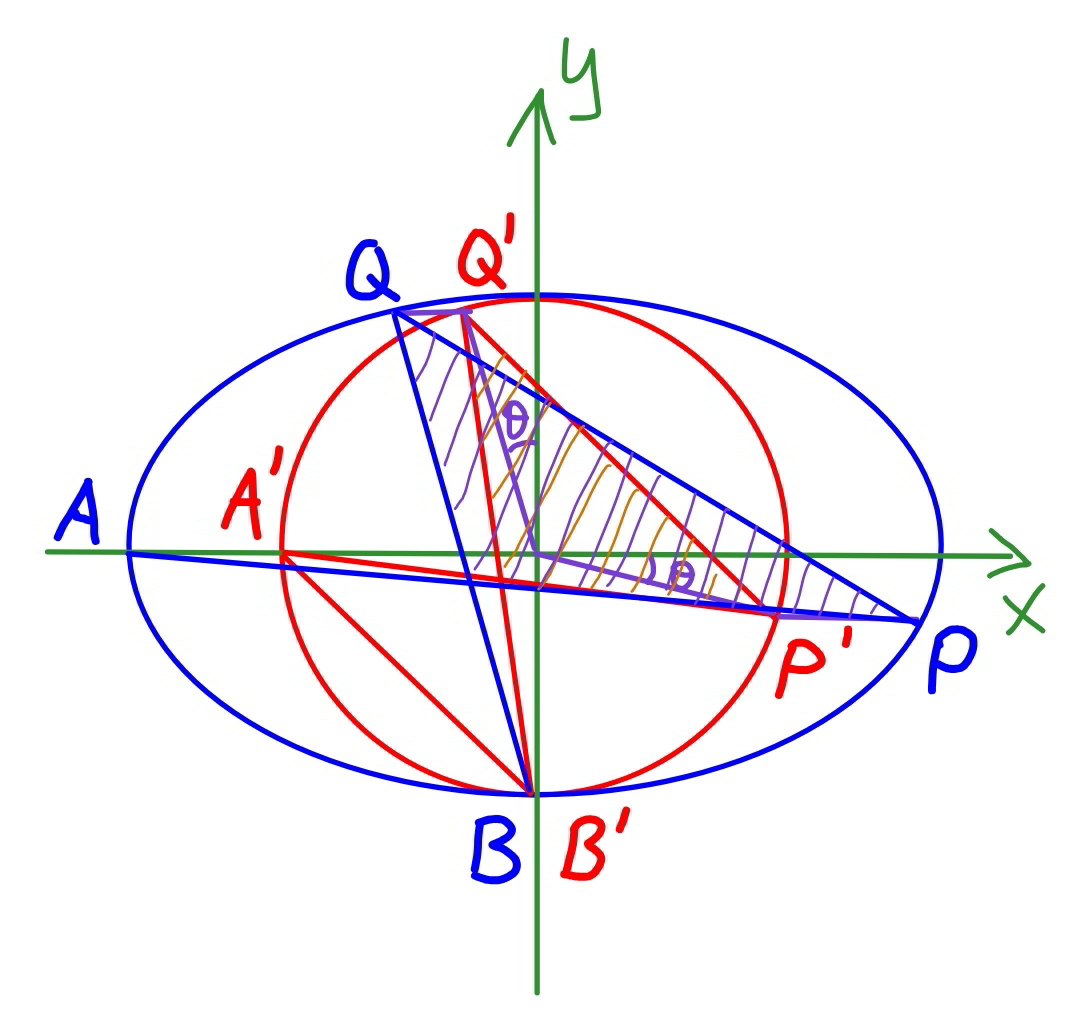
Commented by ajfour last updated on 20/Apr/20
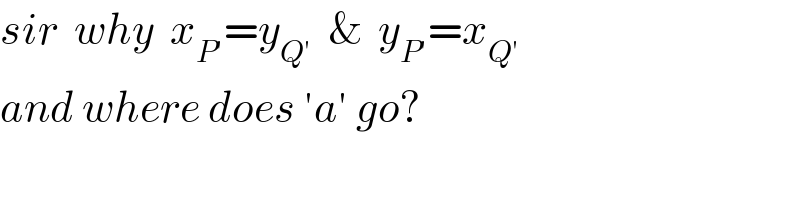
Commented by mr W last updated on 20/Apr/20

Answered by mr W last updated on 19/Apr/20
Commented by mr W last updated on 19/Apr/20
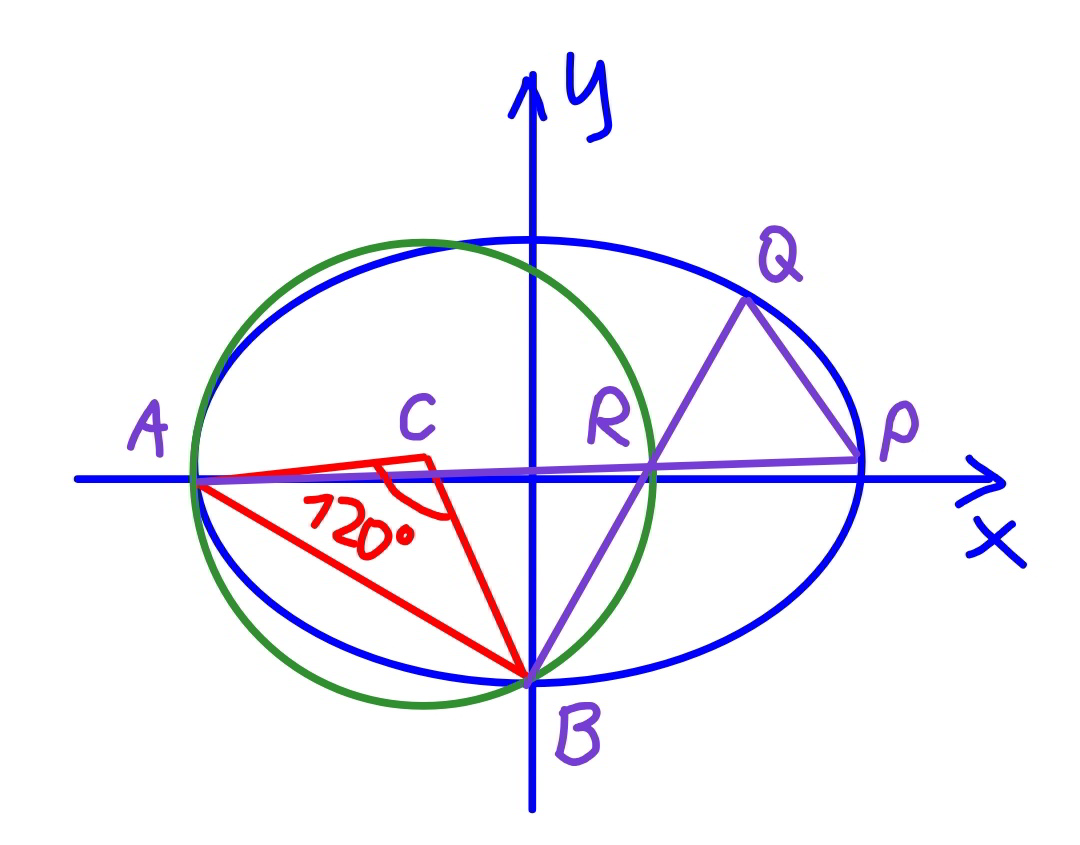
![PART II the point R must lie on the green circle with center at C. let α=tan^(−1) (b/a), μ=(b/a) AC=((AB)/(2 cos 30°))=(√((a^2 +b^2 )/3)) x_C =−a+AC cos (30°−α) x_C =−a+(√((a^2 +b^2 )/3)) (((√3)/2)×(a/(√(a^2 +b^2 )))+(1/2)×(b/(√(a^2 +b^2 )))) ⇒x_C =−(1/2) (a−(b/(√3))) y_C =AC sin (30°−α)=(√((a^2 +b^2 )/3))((1/2)×(a/(√(a^2 +b^2 )))−((√3)/2)×(b/(√(a^2 +b^2 )))) ⇒y_C =(1/2)((a/(√3))−b) eqn. of green circle: [x+(1/2)(a−(b/(√3)))]^2 +[y−(1/2)((a/(√3))−b)]^2 =((a^2 +b^2 )/3) or x_R =−(1/2)(a−(b/(√3)))+(√((a^2 +b^2 )/3)) cos θ y_R =(1/2)((a/(√3))−b)+(√((a^2 +b^2 )/3)) sin θ ⇒(x_R /a)=−(1/2)(1−(μ/(√3)))+(√((1+μ^2 )/3)) cos θ ⇒(y_R /a)=(1/2)((1/(√3))−μ)+(√((1+μ^2 )/3)) sin θ eqn. of AR: y=((a−(√3)b+2(√(a^2 +b^2 )) sin θ)/((√3)a+b+2(√(a^2 +b^2 )) cos θ))(x+a) y=((1−(√3)μ+2(√(1+μ^2 )) sin θ)/((√3)+μ+2(√(1+μ^2 )) cos θ))(x+a) intersection point P: y_P =((1−(√3)μ+2(√(1+μ^2 )) sin θ)/((√3)+μ+2(√(1+μ^2 )) cos θ))(x_P +a) ((x_P /a))^2 +((y_P /b))^2 =1 (((1−(√3)μ+2(√(1+μ^2 )) sin θ)/((√3)+μ+2(√(1+μ^2 )) cos θ)))^2 (1+(x_P /a))^2 =μ^2 [1−((x_P /a))^2 ] (((1−(√3)μ+2(√(1+μ^2 )) sin θ)/((√3)+μ+2(√(1+μ^2 )) cos θ)))^2 (1+(x_P /a))=μ^2 (1−(x_P /a)) ⇒(x_P /a)=((μ^2 −(((1−(√3)μ+2(√(1+μ^2 )) sin θ)/((√3)+μ+2(√(1+μ^2 )) cos θ)))^2 )/(μ^2 +(((1−(√3)μ+2(√(1+μ^2 )) sin θ)/((√3)+μ+2(√(1+μ^2 )) cos θ)))^2 )) ⇒(y_P /a)=(((1−(√3)μ+2(√(1+μ^2 )) sin θ)/((√3)+μ+2(√(1+μ^2 )) cos θ)))(1+(x_P /a)) ((PR^2 )/a^2 )=((x_P /a)−(x_R /a))^2 +((y_P /a)−(y_R /a))^2 eqn. of BR: ((y+b)/(y_R +b))=(x/x_R ) y=−b+((a+(√3)b+2(√(a^2 +b^2 )) sin θ)/(−(√3)a+b+2(√(a^2 +b^2 )) cos θ))x y=−b+((1+(√3)μ+2(√(1+μ^2 )) sin θ)/(−(√3)+μ+2(√(1+μ^2 )) cos θ))x intersection point Q: y_Q =−b+((1+(√3)μ+2(√(1+μ^2 )) sin θ)/(−(√3)+μ+2(√(1+μ^2 )) cos θ))x_Q x_Q =((−(√3)+μ+2(√(1+μ^2 )) cos θ)/(1+(√3)μ+2(√(1+μ^2 )) sin θ))(y_Q +b) ((x_Q /a))^2 +((y_Q /b))^2 =1 μ^2 (((−(√3)+μ+2(√(1+μ^2 )) cos θ)/(1+(√3)μ+2(√(1+μ^2 )) sin θ)))^2 ((y_Q /a)+μ)^2 +((y_Q /a))^2 =μ^2 μ^2 (((−(√3)+μ+2(√(1+μ^2 )) cos θ)/(1+(√3)μ+2(√(1+μ^2 )) sin θ)))^2 ((y_Q /a)+μ)=μ−(y_Q /a) ⇒(y_Q /a)=((μ[1−μ^2 (((−(√3)+μ+2(√(1+μ^2 )) cos θ)/(1+(√3)μ+2(√(1+μ^2 )) sin θ)))^2 ])/(1+μ^2 (((−(√3)+μ+2(√(1+μ^2 )) cos θ)/(1+(√3)μ+2(√(1+μ^2 )) sin θ)))^2 )) ⇒(x_Q /a)=(((−(√3)+μ+2(√(1+μ^2 )) cos θ)/(1+(√3)μ+2(√(1+μ^2 )) sin θ)))((y_Q /a)+μ) ((QR^2 )/a^2 )=((x_Q /a)−(x_R /a))^2 +((y_Q /a)−(y_R /a))^2 such that ΔPQR is equilateral, PR=QR ((PR^2 )/a^2 )=((QR^2 )/a^2 )](Q89894.png)
Commented by mr W last updated on 19/Apr/20
Commented by mr W last updated on 19/Apr/20
Commented by mr W last updated on 20/Apr/20
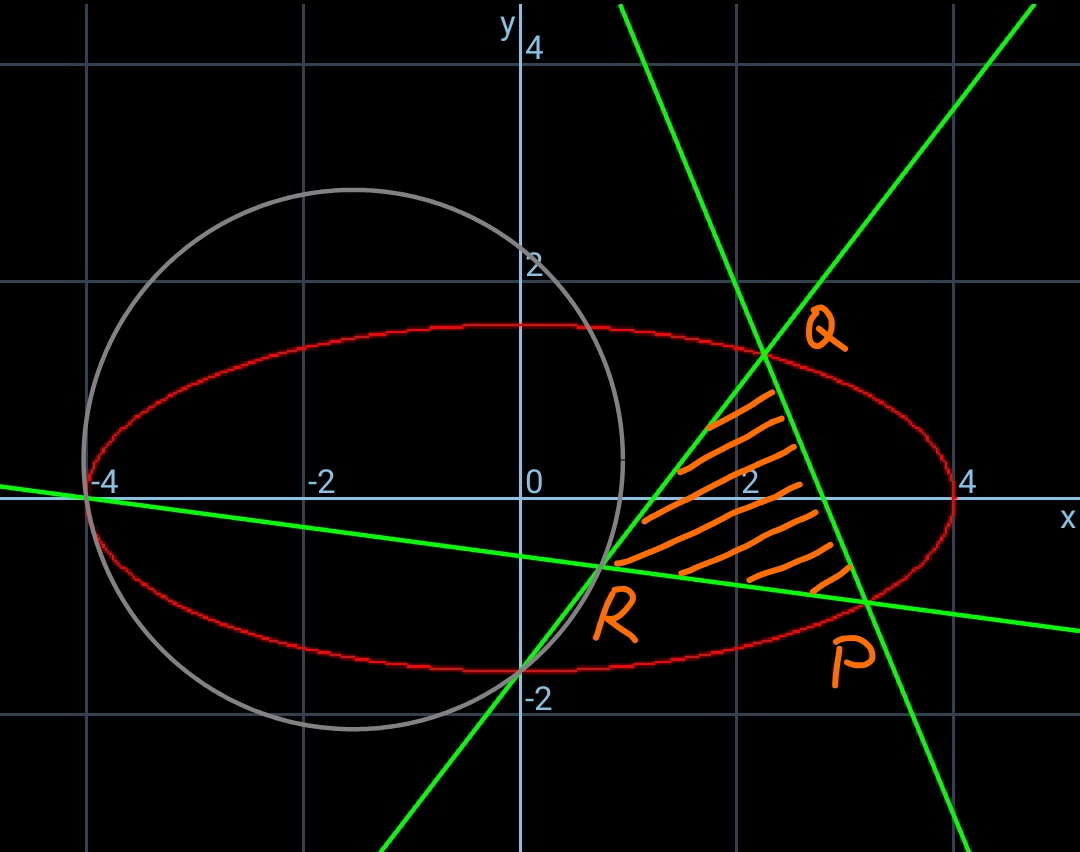
Commented by mr W last updated on 20/Apr/20
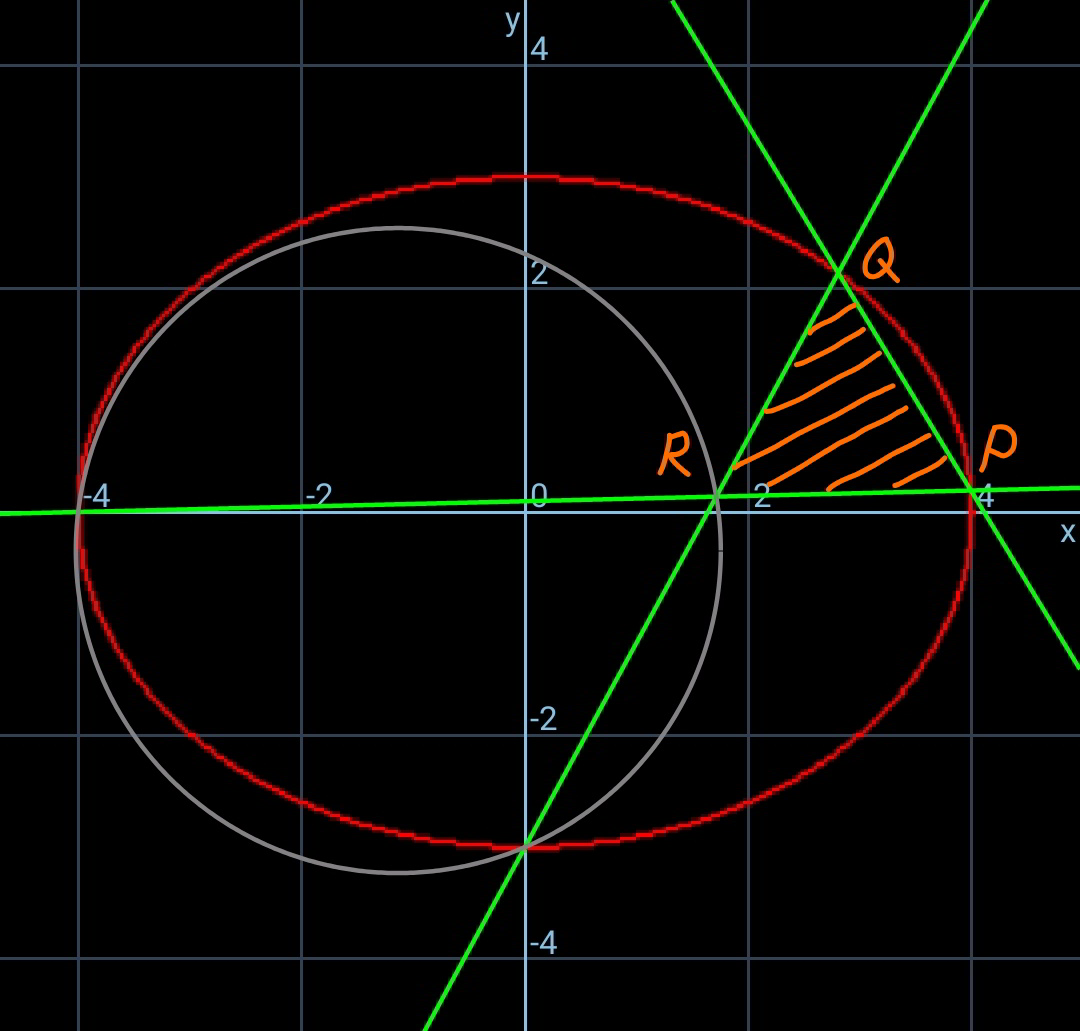
Commented by mr W last updated on 20/Apr/20
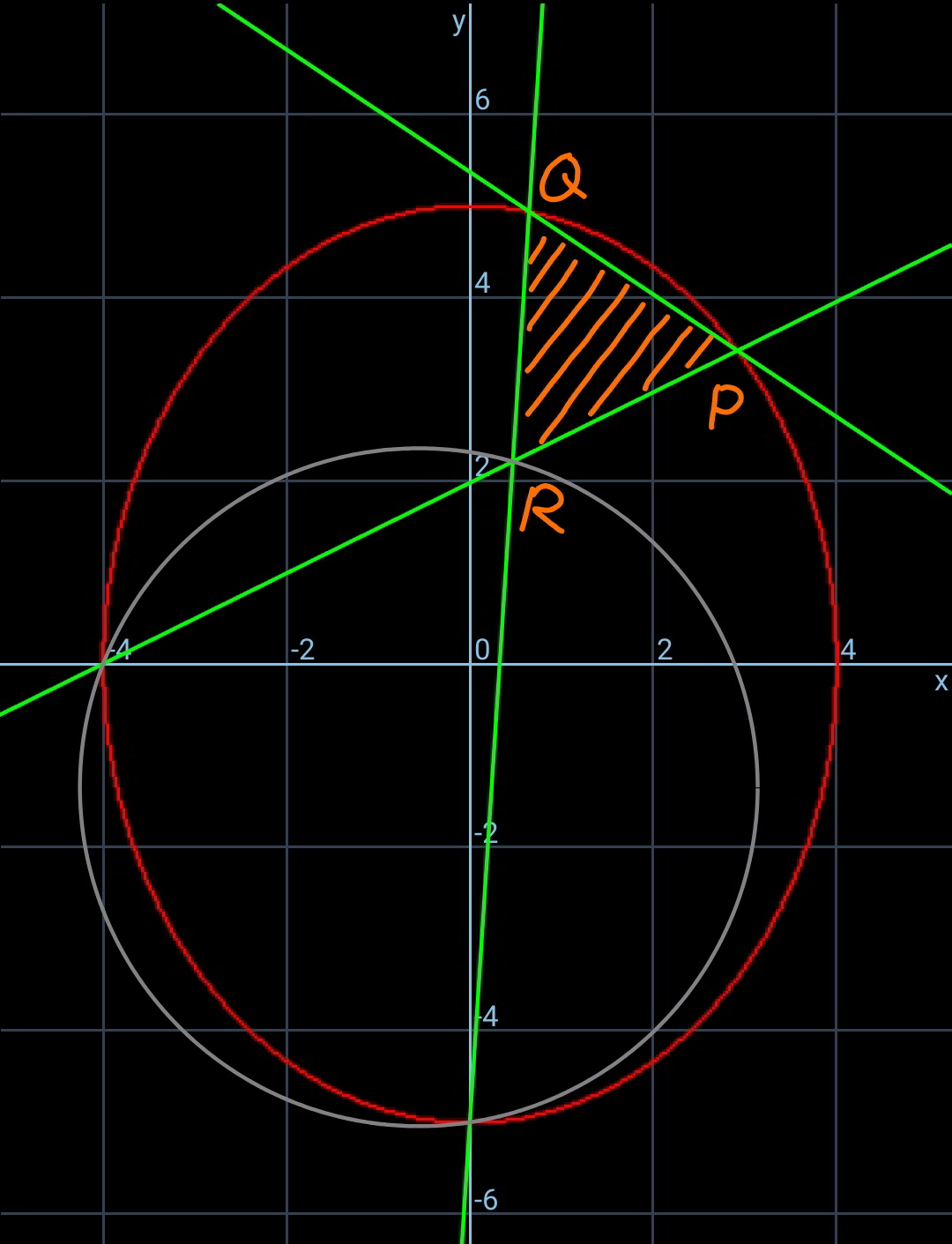
Commented by mr W last updated on 21/Apr/20
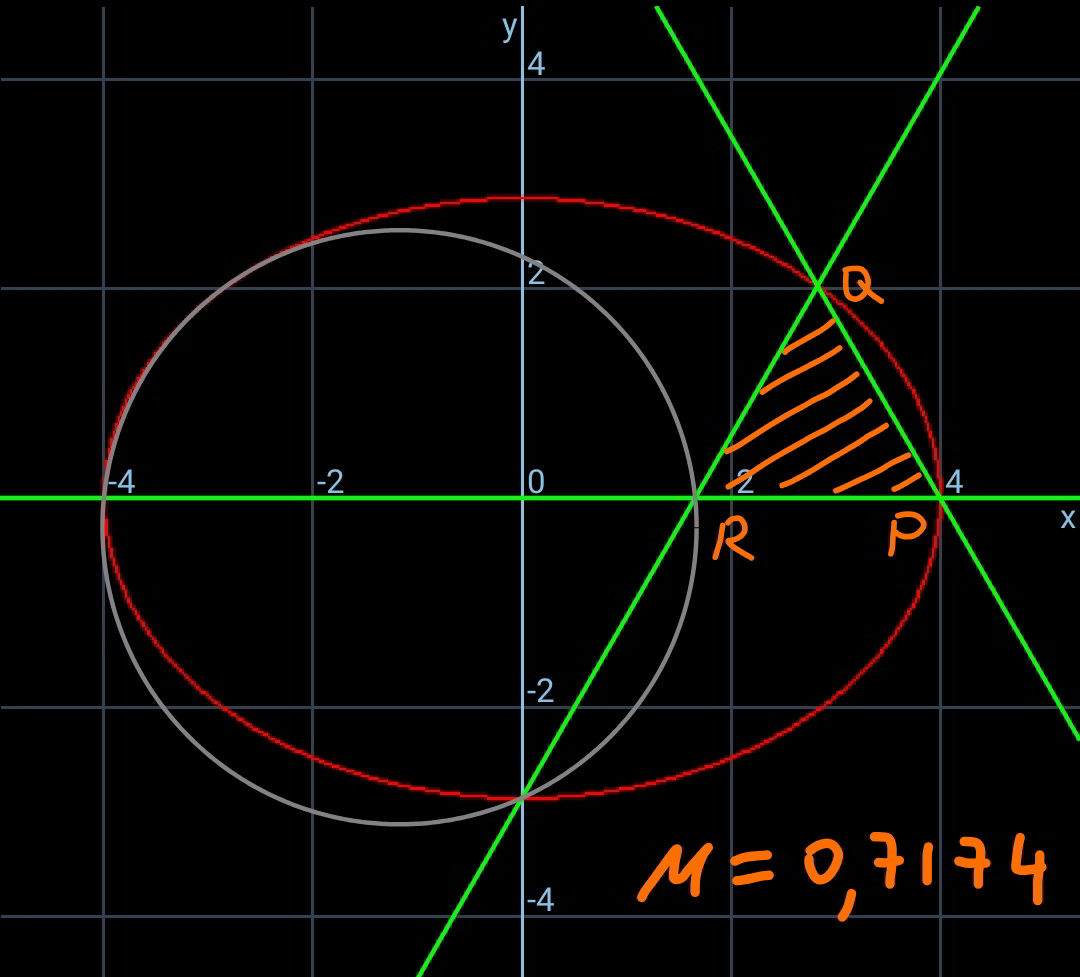
Answered by ajfour last updated on 20/Apr/20
Commented by ajfour last updated on 20/Apr/20
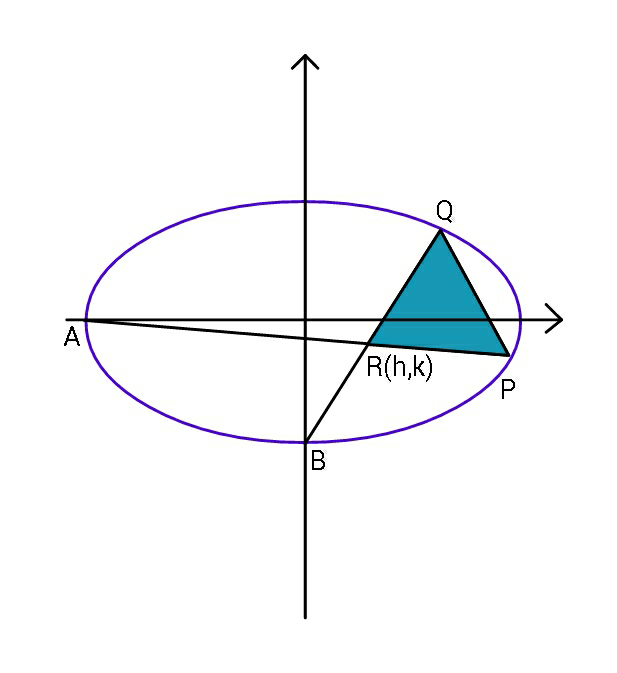
![let R(h,k) Eq. AP: y=((k(x+a))/(h+a)) b^2 x^2 +((k^2 (x+a)^2 a^2 )/((h+a)^2 ))=a^2 b^2 (h+a)^2 b^2 x^2 +k^2 a^2 (x+a)^2 =a^2 b^2 (h+a)^2 roots are x_P , −a ⇒ −ax_P = ((a^2 [a^2 k^2 −b^2 (h+a)^2 ])/(b^2 (h+a)^2 +k^2 a^2 )) x_P =((a[b^2 (h+a)^2 −a^2 k^2 ])/(b^2 (h+a)^2 +k^2 a^2 )) ...(I) Eq. of BQ: y=(((k+b)/h))x−b b^2 h^2 x^2 +a^2 [(k+b)x−bh]^2 =a^2 b^2 h^2 roots are x=0, x_Q x_Q = ((2a^2 bh(k+b))/(b^2 h^2 +a^2 (k+b)^2 )) ...(II) ((((k+b)/h)−(k/(h+a)))/(1+(((k+b)/h))((k/(h+a)))))=(√3) ....(III) slope of PQ: ((y_Q −y_P )/(x_P −x_Q ))=(((√3)−(k/(h+a)))/(1+(√3)((k/(h+a))))) ...(IV) let (k/(h+a))=p , ((k+b)/h)=q x_P =((a[b^2 (h+a)^2 −a^2 k^2 ])/(b^2 (h+a)^2 +k^2 a^2 )) = ((a(b^2 −a^2 p^2 ))/(b^2 +a^2 p^2 )) x_Q =((2a^2 bh(k+b))/(b^2 h^2 +a^2 (k+b)^2 )) = ((2a^2 bq)/(b^2 +a^2 q^2 )) y_P =p(x_P +a)=((p(2ab^2 ))/(b^2 +a^2 p^2 )) y_Q =qx_Q −b = ((2a^2 bq^2 )/(b^2 +a^2 q^2 ))−b =((b(a^2 q^2 −b^2 ))/(b^2 +a^2 q^2 )) ((((b(a^2 q^2 −b^2 ))/(b^2 +a^2 q^2 ))−((p(2ab^2 ))/(b^2 +a^2 p^2 )))/(((a(b^2 −a^2 p^2 ))/(b^2 +a^2 p^2 ))−((2a^2 bq)/(b^2 +a^2 q^2 ))))=(((√3)−p)/(1+p(√3))) ......(i) And ((q−p)/(1+pq))=(√3) .......(ii) ((b(a^2 q^2 −b^2 )(b^2 +a^2 p^2 )−2ab^2 p(b^2 +a^2 q^2 ))/(a(b^2 −a^2 p^2 )(b^2 +a^2 q^2 )+2a^2 bq(b^2 +a^2 p^2 ))) = (((√3)−p)/(1+p(√3))) ....](Q89960.png)
Commented by mr W last updated on 20/Apr/20
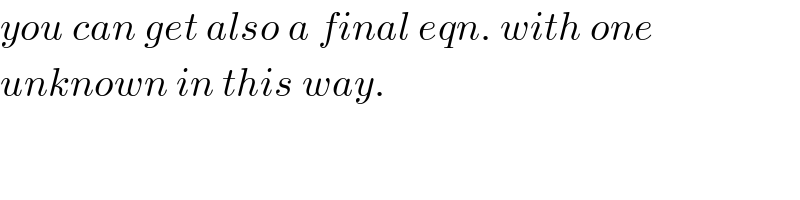
Commented by ajfour last updated on 21/Apr/20