
Question and Answers Forum
Question Number 89918 by jagoll last updated on 20/Apr/20
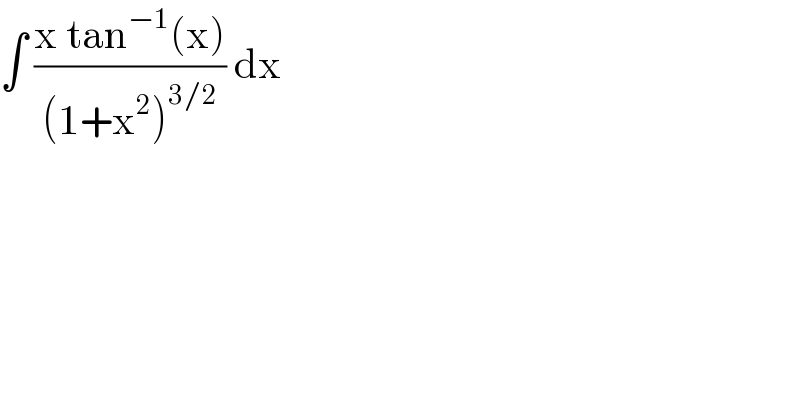
Commented by john santu last updated on 20/Apr/20
![[ u = tan^(−1) (x) ⇒du = (dx/(1+x^2 ))] v = ∫ ((x dx)/((1+x^2 )^(3/2) )) = (1/2)∫ ((d(1+x^2 ))/((1+x^2 )^(3/2) )) v = − (1/(√(1+x^2 ))) ] ⇒ I = −((tan^(−1) (x))/(√(1+x^2 ))) + ∫ (dx/((1+x^2 )^(3/2) )) let J = ∫ (dx/((1+x^2 )^(3/2) )) x = tan p ⇒dx = sec^2 p dp J = ∫ ((sec^2 p dp)/(sec^3 p)) = ∫ cos p dp J = sin p = (x/(√(1+x^2 ))) therefore we get ∫ ((x tan^(−1) (x) dx)/((1+x^2 )^(3/2) )) = −((tan^(−1) (x))/(√(1+x^2 ))) +(x/(√(1+x^2 ))) + c = ((x−tan^(−1) (x))/(√(1+x^2 ))) + c](Q89921.png)
| ||
Question and Answers Forum | ||
Question Number 89918 by jagoll last updated on 20/Apr/20 | ||
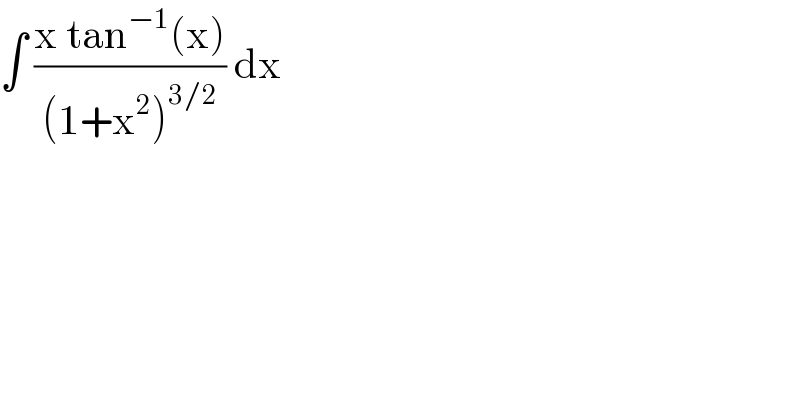 | ||
Commented by john santu last updated on 20/Apr/20 | ||
![[ u = tan^(−1) (x) ⇒du = (dx/(1+x^2 ))] v = ∫ ((x dx)/((1+x^2 )^(3/2) )) = (1/2)∫ ((d(1+x^2 ))/((1+x^2 )^(3/2) )) v = − (1/(√(1+x^2 ))) ] ⇒ I = −((tan^(−1) (x))/(√(1+x^2 ))) + ∫ (dx/((1+x^2 )^(3/2) )) let J = ∫ (dx/((1+x^2 )^(3/2) )) x = tan p ⇒dx = sec^2 p dp J = ∫ ((sec^2 p dp)/(sec^3 p)) = ∫ cos p dp J = sin p = (x/(√(1+x^2 ))) therefore we get ∫ ((x tan^(−1) (x) dx)/((1+x^2 )^(3/2) )) = −((tan^(−1) (x))/(√(1+x^2 ))) +(x/(√(1+x^2 ))) + c = ((x−tan^(−1) (x))/(√(1+x^2 ))) + c](Q89921.png) | ||