Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 90069 by ajfour last updated on 21/Apr/20

Commented by ajfour last updated on 21/Apr/20

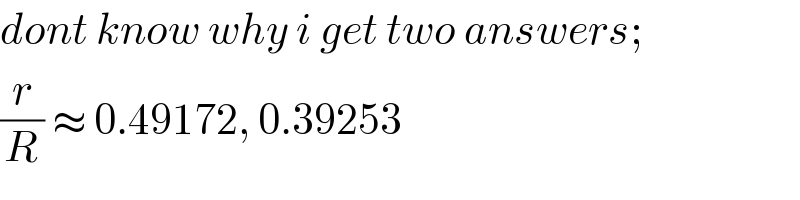
dont know why i get two answers; (r/R) ≈ 0.49172, 0.39253

$${dont}\:{know}\:{why}\:{i}\:{get}\:{two}\:{answers}; \\ $$$$\frac{{r}}{{R}}\:\approx\:\mathrm{0}.\mathrm{49172},\:\mathrm{0}.\mathrm{39253} \\ $$

Commented by ajfour last updated on 21/Apr/20

Find r/R.

$${Find}\:{r}/{R}. \\ $$

Commented by ajfour last updated on 21/Apr/20

mrW Sir, please attempt..

$${mrW}\:{Sir},\:{please}\:{attempt}.. \\ $$

Answered by mr W last updated on 21/Apr/20

Commented by mr W last updated on 21/Apr/20

with λ=(R/r) α+β=(π/2) sin (β/2)=(r/(R−r))=(1/(λ−1)) ⇒cos (β/2)=(√(1−(1/((λ−1)^2 ))))=((√(λ^2 −2λ))/(λ−1)) ⇒tan (β/2)=(1/(√(λ^2 −2λ))) ⇒cos β=1−(2/((λ−1)^2 )) OB=(R/(cos β)) OC=(√((R+r)^2 −r^2 ))=(√(R^2 +2Rr)) CB=(R/(cos β))−(√(R^2 +2Rr)) tan (α/2)=(r/((R/(cos β))−(√(R^2 +2Rr)))) ((1−tan (β/2))/(1+tan (β/2)))=(1/((λ/(cos β))−(√(λ^2 +2λ)))) (2/(1+(1/(√(λ^2 −2λ)))))−1=(1/((λ/(1−(2/((λ−1)^2 ))))−(√(λ^2 +2λ)))) ⇒(((√(λ^2 −2λ))−1)/(1+(√(λ^2 −2λ))))=((λ^2 −2λ−1)/(λ(λ−1)^2 −(λ^2 −2λ−1)(√(λ^2 +2λ)))) ⇒(1+(√(λ^2 −2λ)))^2 =λ(λ−1)^2 −(λ^2 −2λ−1)(√(λ^2 +2λ)) ⇒2(√(λ^2 −2λ))+(λ^2 −2λ−1)(√(λ^2 +2λ))=(λ−1)^3 ⇒λ=(R/r)=2.4142 or 2.5475 ⇒(r/R)=0.4142 or 0.3925

$${with}\:\lambda=\frac{{R}}{{r}} \\ $$$$\alpha+\beta=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\frac{\beta}{\mathrm{2}}=\frac{{r}}{{R}−{r}}=\frac{\mathrm{1}}{\lambda−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{cos}\:\frac{\beta}{\mathrm{2}}=\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\left(\lambda−\mathrm{1}\right)^{\mathrm{2}} }}=\frac{\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}\lambda}}{\lambda−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\beta}{\mathrm{2}}=\frac{\mathrm{1}}{\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}\lambda}} \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\mathrm{1}−\frac{\mathrm{2}}{\left(\lambda−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${OB}=\frac{{R}}{\mathrm{cos}\:\beta} \\ $$$${OC}=\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }=\sqrt{{R}^{\mathrm{2}} +\mathrm{2}{Rr}} \\ $$$${CB}=\frac{{R}}{\mathrm{cos}\:\beta}−\sqrt{{R}^{\mathrm{2}} +\mathrm{2}{Rr}} \\ $$$$\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\frac{{r}}{\frac{{R}}{\mathrm{cos}\:\beta}−\sqrt{{R}^{\mathrm{2}} +\mathrm{2}{Rr}}} \\ $$$$\frac{\mathrm{1}−\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}=\frac{\mathrm{1}}{\frac{\lambda}{\mathrm{cos}\:\beta}−\sqrt{\lambda^{\mathrm{2}} +\mathrm{2}\lambda}} \\ $$$$\frac{\mathrm{2}}{\mathrm{1}+\frac{\mathrm{1}}{\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}\lambda}}}−\mathrm{1}=\frac{\mathrm{1}}{\frac{\lambda}{\mathrm{1}−\frac{\mathrm{2}}{\left(\lambda−\mathrm{1}\right)^{\mathrm{2}} }}−\sqrt{\lambda^{\mathrm{2}} +\mathrm{2}\lambda}} \\ $$$$\Rightarrow\frac{\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}\lambda}−\mathrm{1}}{\mathrm{1}+\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}\lambda}}=\frac{\lambda^{\mathrm{2}} −\mathrm{2}\lambda−\mathrm{1}}{\lambda\left(\lambda−\mathrm{1}\right)^{\mathrm{2}} −\left(\lambda^{\mathrm{2}} −\mathrm{2}\lambda−\mathrm{1}\right)\sqrt{\lambda^{\mathrm{2}} +\mathrm{2}\lambda}} \\ $$$$\Rightarrow\left(\mathrm{1}+\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}\lambda}\right)^{\mathrm{2}} =\lambda\left(\lambda−\mathrm{1}\right)^{\mathrm{2}} −\left(\lambda^{\mathrm{2}} −\mathrm{2}\lambda−\mathrm{1}\right)\sqrt{\lambda^{\mathrm{2}} +\mathrm{2}\lambda} \\ $$$$\Rightarrow\mathrm{2}\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}\lambda}+\left(\lambda^{\mathrm{2}} −\mathrm{2}\lambda−\mathrm{1}\right)\sqrt{\lambda^{\mathrm{2}} +\mathrm{2}\lambda}=\left(\lambda−\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\Rightarrow\lambda=\frac{{R}}{{r}}=\mathrm{2}.\mathrm{4142}\:{or}\:\mathrm{2}.\mathrm{5475} \\ $$$$\Rightarrow\frac{{r}}{{R}}=\mathrm{0}.\mathrm{4142}\:{or}\:\mathrm{0}.\mathrm{3925} \\ $$

Commented by ajfour last updated on 21/Apr/20

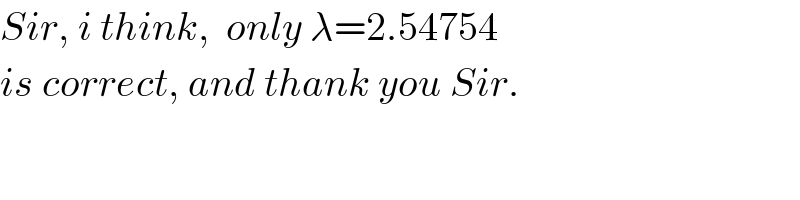
Sir, i think, only λ=2.54754 is correct, and thank you Sir.

$${Sir},\:{i}\:{think},\:\:{only}\:\lambda=\mathrm{2}.\mathrm{54754} \\ $$$${is}\:{correct},\:{and}\:{thank}\:{you}\:{Sir}. \\ $$

Answered by ajfour last updated on 21/Apr/20

Commented by ajfour last updated on 21/Apr/20

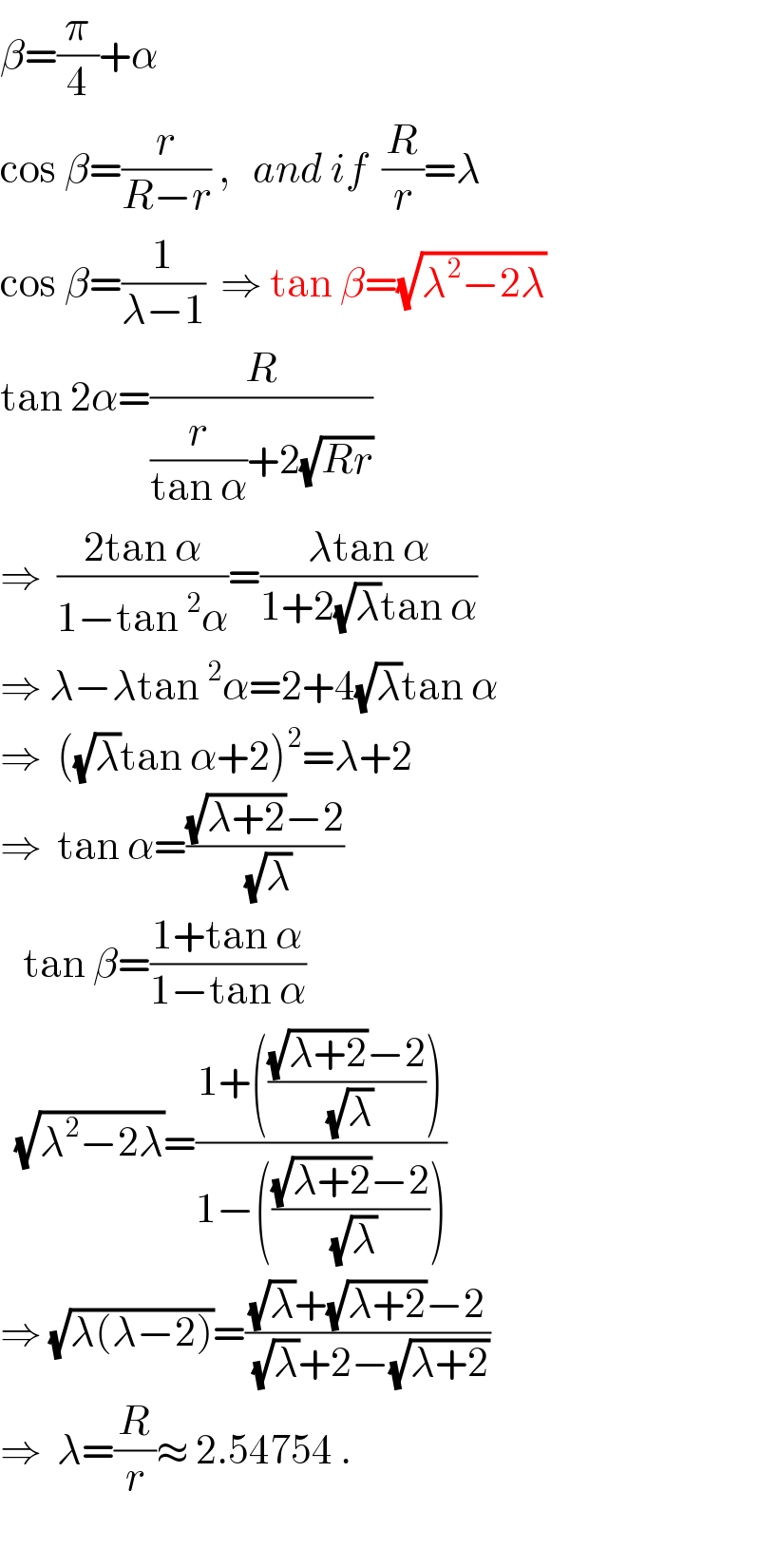
β=(π/4)+α cos β=(r/(R−r)) , and if (R/r)=λ cos β=(1/(λ−1)) ⇒ tan β=(√(λ^2 −2λ)) tan 2α=(R/((r/(tan α))+2(√(Rr)))) ⇒ ((2tan α)/(1−tan^2 α))=((λtan α)/(1+2(√λ)tan α)) ⇒ λ−λtan^2 α=2+4(√λ)tan α ⇒ ((√λ)tan α+2)^2 =λ+2 ⇒ tan α=(((√(λ+2))−2)/(√λ)) tan β=((1+tan α)/(1−tan α)) (√(λ^2 −2λ))=((1+((((√(λ+2))−2)/(√λ))))/(1−((((√(λ+2))−2)/(√λ))))) ⇒ (√(λ(λ−2)))=(((√λ)+(√(λ+2))−2)/((√λ)+2−(√(λ+2)))) ⇒ λ=(R/r)≈ 2.54754 .

$$\beta=\frac{\pi}{\mathrm{4}}+\alpha \\ $$$$\mathrm{cos}\:\beta=\frac{{r}}{{R}−{r}}\:,\:\:\:{and}\:{if}\:\:\frac{{R}}{{r}}=\lambda \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{1}}{\lambda−\mathrm{1}}\:\:\Rightarrow\:\mathrm{tan}\:\beta=\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}\lambda} \\ $$$$\mathrm{tan}\:\mathrm{2}\alpha=\frac{{R}}{\frac{{r}}{\mathrm{tan}\:\alpha}+\mathrm{2}\sqrt{{Rr}}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{2tan}\:\alpha}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \alpha}=\frac{\lambda\mathrm{tan}\:\alpha}{\mathrm{1}+\mathrm{2}\sqrt{\lambda}\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow\:\lambda−\lambda\mathrm{tan}\:^{\mathrm{2}} \alpha=\mathrm{2}+\mathrm{4}\sqrt{\lambda}\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\:\:\left(\sqrt{\lambda}\mathrm{tan}\:\alpha+\mathrm{2}\right)^{\mathrm{2}} =\lambda+\mathrm{2} \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\alpha=\frac{\sqrt{\lambda+\mathrm{2}}−\mathrm{2}}{\sqrt{\lambda}} \\ $$$$\:\:\:\mathrm{tan}\:\beta=\frac{\mathrm{1}+\mathrm{tan}\:\alpha}{\mathrm{1}−\mathrm{tan}\:\alpha} \\ $$$$\:\:\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}\lambda}=\frac{\mathrm{1}+\left(\frac{\sqrt{\lambda+\mathrm{2}}−\mathrm{2}}{\sqrt{\lambda}}\right)}{\mathrm{1}−\left(\frac{\sqrt{\lambda+\mathrm{2}}−\mathrm{2}}{\sqrt{\lambda}}\right)} \\ $$$$\Rightarrow\:\sqrt{\lambda\left(\lambda−\mathrm{2}\right)}=\frac{\sqrt{\lambda}+\sqrt{\lambda+\mathrm{2}}−\mathrm{2}}{\sqrt{\lambda}+\mathrm{2}−\sqrt{\lambda+\mathrm{2}}} \\ $$$$\Rightarrow\:\:\lambda=\frac{{R}}{{r}}\approx\:\mathrm{2}.\mathrm{54754}\:. \\ $$$$\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com