
Question Number 9009 by tawakalitu last updated on 13/Nov/16
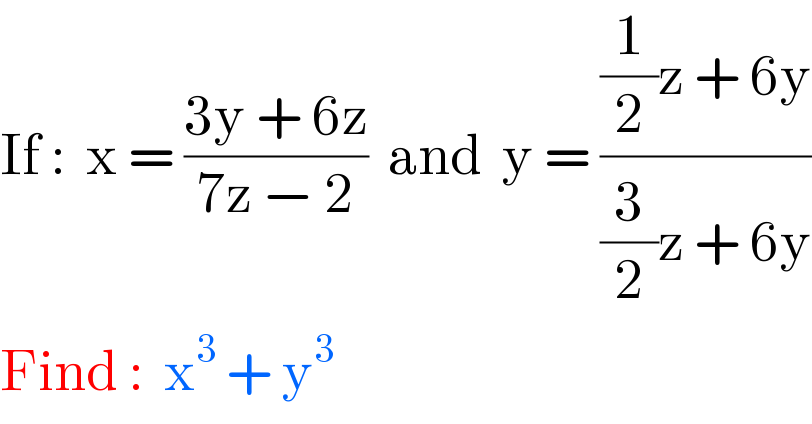
$$\mathrm{If}\::\:\:\mathrm{x}\:=\:\frac{\mathrm{3y}\:+\:\mathrm{6z}}{\mathrm{7z}\:−\:\mathrm{2}}\:\:\mathrm{and}\:\:\mathrm{y}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{z}\:+\:\mathrm{6y}}{\frac{\mathrm{3}}{\mathrm{2}}\mathrm{z}\:+\:\mathrm{6y}} \\ $$$$\mathrm{Find}\::\:\:\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{y}^{\mathrm{3}} \\ $$
Answered by Rasheed Soomro last updated on 14/Nov/16

$$\mathrm{If}\::\:\:\mathrm{x}\:=\:\frac{\mathrm{3y}\:+\:\mathrm{6z}}{\mathrm{7z}\:−\:\mathrm{2}}\:\:\mathrm{and}\:\:\mathrm{y}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{z}\:+\:\mathrm{6y}}{\frac{\mathrm{3}}{\mathrm{2}}\mathrm{z}\:+\:\mathrm{6y}}=\frac{\mathrm{z}+\mathrm{12y}}{\mathrm{3z}+\mathrm{12y}} \\ $$$$\mathrm{y}=\frac{\mathrm{z}+\mathrm{12y}}{\mathrm{3z}+\mathrm{12y}}\Rightarrow\mathrm{3yz}+\mathrm{12y}^{\mathrm{2}} =\mathrm{z}+\mathrm{12y} \\ $$$$\mathrm{12y}^{\mathrm{2}} +\mathrm{3}\left(\mathrm{z}−\mathrm{4}\right)\mathrm{y}−\mathrm{z}=\mathrm{0} \\ $$$$\mathrm{y}=\frac{−\mathrm{3}\left(\mathrm{z}−\mathrm{4}\right)\pm\sqrt{\mathrm{9}\left(\mathrm{z}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{48z}}}{\mathrm{24}} \\ $$$$\:\:\:\:=\frac{−\mathrm{3}\left(\mathrm{z}−\mathrm{4}\right)\pm\sqrt{\mathrm{9z}^{\mathrm{2}} −\mathrm{24z}+\mathrm{144}}}{\mathrm{24}} \\ $$$$−−−− \\ $$$$\mathrm{x}\:=\:\frac{\mathrm{3y}\:+\:\mathrm{6z}}{\mathrm{7z}\:−\:\mathrm{2}}\:=\frac{\mathrm{3}\left(\frac{−\mathrm{3}\left(\mathrm{z}−\mathrm{4}\right)\pm\sqrt{\mathrm{9z}^{\mathrm{2}} −\mathrm{24z}+\mathrm{144}}}{\mathrm{24}}\right)+\mathrm{6z}}{\mathrm{7z}−\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{\frac{−\mathrm{3}\left(\mathrm{z}−\mathrm{4}\right)\pm\sqrt{\mathrm{9z}^{\mathrm{2}} −\mathrm{24z}+\mathrm{144}}}{\mathrm{8}}+\mathrm{6z}}{\mathrm{7z}−\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{\frac{−\mathrm{3}\left(\mathrm{z}−\mathrm{4}\right)\pm\sqrt{\mathrm{9z}^{\mathrm{2}} −\mathrm{24z}+\mathrm{144}}+\mathrm{48z}}{\mathrm{8}}}{\mathrm{7z}−\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{45z}+\mathrm{12}\pm\sqrt{\mathrm{9z}^{\mathrm{2}} −\mathrm{24z}+\mathrm{144}}}{\mathrm{8}\left(\mathrm{7z}−\mathrm{2}\right)} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} =\left(\frac{\mathrm{45z}+\mathrm{12}\pm\sqrt{\mathrm{9z}^{\mathrm{2}} −\mathrm{24z}+\mathrm{144}}}{\mathrm{8}\left(\mathrm{7z}−\mathrm{2}\right)}\right)^{\mathrm{3}} +\left(\frac{−\mathrm{3}\left(\mathrm{z}−\mathrm{4}\right)\pm\sqrt{\mathrm{9z}^{\mathrm{2}} −\mathrm{24z}+\mathrm{144}}}{\mathrm{24}}\right)^{\mathrm{3}} \\ $$$$\: \\ $$
Commented by tawakalitu last updated on 13/Nov/16
$$\mathrm{thanks}\:\mathrm{sir}.\:\mathrm{will}\:\mathrm{be}\:\mathrm{expecting}. \\ $$
Commented by tawakalitu last updated on 14/Nov/16
$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
