Question Number 90307 by niroj last updated on 22/Apr/20
$$\:\:\boldsymbol{\mathrm{Solve}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{differential}}\:\boldsymbol{\mathrm{equation}}. \\ $$$$\:\:\:\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{D}}^{\mathrm{2}} −\mathrm{2}\right)\boldsymbol{\mathrm{y}}\:=\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:+\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}. \\ $$
Answered by TANMAY PANACEA. last updated on 22/Apr/20
![x^2 (d^2 y/dx^2 )−2y=x^2 +(1/x) x=e^t (dy/dx)=(dy/dt)×(dt/dx)=(1/e^t )(dy/dt) (d/dx)((dy/dx))=(d/dt)((1/e^t )×(dy/dt))×(dt/dx)=(1/e^t )[(1/e^t )×(d^2 y/dt^2 )−(1/e^t )×(dy/dt)] (e^t )^2 (d^2 y/dx^2 )=(d^2 y/dt^2 )−(dy/dt) x^2 (d^2 y/dx^2 )=(d^2 y/dt^2 )−(dy/dt) so (d^2 y/dt^2 )−(dy/dt)−2y=e^(2t) +e^(−t) let y=e^(mt) (m^2 −m−2)e^(mt) =0 for C.F (m−2)(m+1)=0 C.F=Ae^(2t) +Be^(−t) =Ax^2 +(B/x) P.I let (d/dt)=θ y=((e^(2t) +e^(−t) )/((θ^2 −θ−2)))=((x^2 +(1/x))/((θ−2)(θ+1)))=(1/3)×(((θ+1)−(θ−2))/((θ−2)(θ+1)))×(x^2 +(1/x)) =(1/3)[(1/(θ−2))−(1/(θ+1))](x^2 +(1/x)) =(1/3)×[x^2 ∫x^(−2−1) (x^2 +(1/x))dx−x^(−1) ∫x^(1−1) (x^2 +(1/x))dx] =(1/3)[x^2 ∫((1/x)+(1/x^4 ))dx−(1/x)∫(x^2 +(1/x))dx] =(1/3)[x^2 ×lnx+x^2 ×(1/(x^3 ×(−3)))−(1/x)×(x^3 /3)−(1/x)lnx] =((x^2 lnx)/3)−(1/9)×(1/x)−(x^2 /9)−((lnx)/(3x)) =(x^2 −(1/x))×((lnx)/3)−(1/9)(x^2 +(1/x)) y=Ax^2 +(B/x)+((x^2 lnx)/3)−((lnx)/(3x))−(x^2 /9)−(1/(9x)) y=C_1 x^2 +(C_2 /x)+((x^2 lnx)/3)−((lnx)/(3x))](Q90313.png)
$${x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }−\mathrm{2}{y}={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}} \\ $$$${x}={e}^{{t}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}}×\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{{e}^{{t}} }\frac{{dy}}{{dt}} \\ $$$$\frac{{d}}{{dx}}\left(\frac{{dy}}{{dx}}\right)=\frac{{d}}{{dt}}\left(\frac{\mathrm{1}}{{e}^{{t}} }×\frac{{dy}}{{dt}}\right)×\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{{e}^{{t}} }\left[\frac{\mathrm{1}}{{e}^{{t}} }×\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{\mathrm{1}}{{e}^{{t}} }×\frac{{dy}}{{dt}}\right] \\ $$$$\left({e}^{{t}} \right)^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{{dy}}{{dt}} \\ $$$${x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{{dy}}{{dt}} \\ $$$$\boldsymbol{{so}} \\ $$$$\frac{\boldsymbol{{d}}^{\mathrm{2}} \boldsymbol{{y}}}{\boldsymbol{{dt}}^{\mathrm{2}} }−\frac{\boldsymbol{{dy}}}{\boldsymbol{{dt}}}−\mathrm{2}\boldsymbol{{y}}=\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{t}}} +\boldsymbol{{e}}^{−\boldsymbol{{t}}} \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{y}}=\boldsymbol{{e}}^{\boldsymbol{{mt}}} \\ $$$$\left(\boldsymbol{{m}}^{\mathrm{2}} −\boldsymbol{{m}}−\mathrm{2}\right)\boldsymbol{{e}}^{\boldsymbol{{mt}}} =\mathrm{0}\:\:\:\boldsymbol{{for}}\:\boldsymbol{{C}}.{F} \\ $$$$\left({m}−\mathrm{2}\right)\left({m}+\mathrm{1}\right)=\mathrm{0} \\ $$$${C}.{F}={Ae}^{\mathrm{2}{t}} +{Be}^{−{t}} =\boldsymbol{{A}}{x}^{\mathrm{2}} +\frac{{B}}{{x}} \\ $$$${P}.{I} \\ $$$${let}\:\frac{{d}}{{dt}}=\theta \\ $$$${y}=\frac{{e}^{\mathrm{2}{t}} +{e}^{−{t}} }{\left(\theta^{\mathrm{2}} −\theta−\mathrm{2}\right)}=\frac{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}}}{\left(\theta−\mathrm{2}\right)\left(\theta+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\left(\theta+\mathrm{1}\right)−\left(\theta−\mathrm{2}\right)}{\left(\theta−\mathrm{2}\right)\left(\theta+\mathrm{1}\right)}×\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{1}}{\theta−\mathrm{2}}−\frac{\mathrm{1}}{\theta+\mathrm{1}}\right]\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\left[{x}^{\mathrm{2}} \int{x}^{−\mathrm{2}−\mathrm{1}} \left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}}\right){dx}−{x}^{−\mathrm{1}} \int{x}^{\mathrm{1}−\mathrm{1}} \left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}}\right){dx}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[{x}^{\mathrm{2}} \int\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right){dx}−\frac{\mathrm{1}}{{x}}\int\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}}\right){dx}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[{x}^{\mathrm{2}} ×{lnx}+{x}^{\mathrm{2}} ×\frac{\mathrm{1}}{{x}^{\mathrm{3}} ×\left(−\mathrm{3}\right)}−\frac{\mathrm{1}}{{x}}×\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{1}}{{x}}{lnx}\right] \\ $$$$=\frac{{x}^{\mathrm{2}} {lnx}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{9}}×\frac{\mathrm{1}}{{x}}−\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\frac{{lnx}}{\mathrm{3}{x}} \\ $$$$=\left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{{x}}\right)×\frac{{lnx}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{9}}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}}\right) \\ $$$${y}={Ax}^{\mathrm{2}} +\frac{{B}}{{x}}+\frac{{x}^{\mathrm{2}} {lnx}}{\mathrm{3}}−\frac{{lnx}}{\mathrm{3}{x}}−\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{9}{x}} \\ $$$${y}={C}_{\mathrm{1}} {x}^{\mathrm{2}} +\frac{{C}_{\mathrm{2}} }{{x}}+\frac{{x}^{\mathrm{2}} {lnx}}{\mathrm{3}}−\frac{{lnx}}{\mathrm{3}{x}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by niroj last updated on 22/Apr/20
$$\mathrm{I}\:\mathrm{apriciate}\:\mathrm{your}\:\mathrm{trying}\:\mathrm{effort}\:\mathrm{but}\: \\ $$$$\:\mathrm{Answer}\:\mathrm{should}\:\mathrm{make}\:\mathrm{sure} \\ $$$$\:\:\boldsymbol{\mathrm{y}}=\:\boldsymbol{\mathrm{C}}_{\mathrm{1}} \mathrm{x}^{−\mathrm{1}} +\mathrm{C}_{\mathrm{2}} \boldsymbol{\mathrm{x}}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{log}}\:\boldsymbol{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{3}\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{log}}\:\boldsymbol{\mathrm{x}}. \\ $$
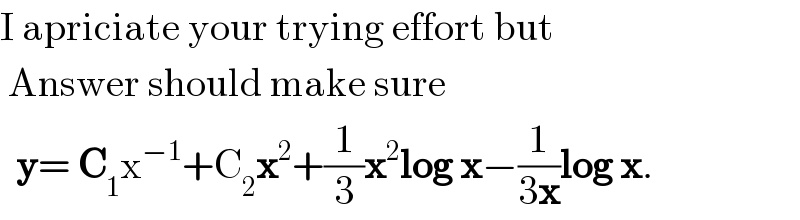
Commented by TANMAY PANACEA. last updated on 22/Apr/20
$${i}\:{have}\:{corrected}...{using}\:{Daniel}\:{and}\:{murry}\:{diff} \\ $$$${cal}\:{book} \\ $$
Commented by niroj last updated on 23/Apr/20
$$\:\mathrm{now}\:\mathrm{done}\:\mathrm{dear}\:. \\ $$