Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 90457 by M±th+et£s last updated on 23/Apr/20

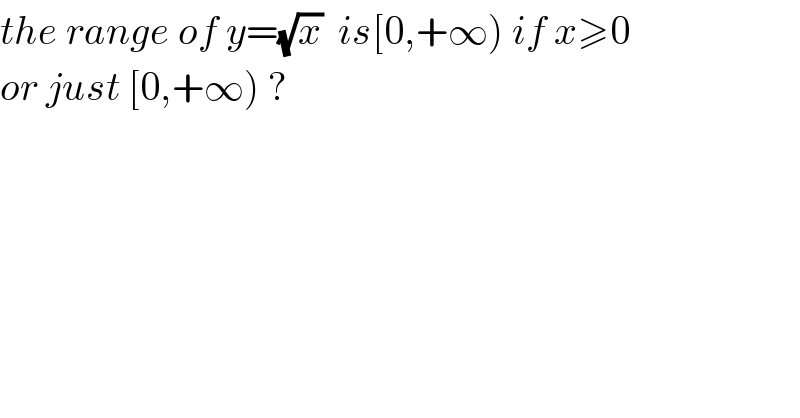
the range of y=(√x) is[0,+∞) if x≥0 or just [0,+∞) ?

$${the}\:{range}\:{of}\:{y}=\sqrt{{x}}\:\:{is}\left[\mathrm{0},+\infty\right)\:{if}\:{x}\geqslant\mathrm{0} \\ $$$${or}\:{just}\:\left[\mathrm{0},+\infty\right)\:? \\ $$

Commented by MJS last updated on 24/Apr/20

talking of “definition” and “range” makes no sense for x∉R usually. y=(√x) is defined for x≥0 and its range is [0; +∞) for x∈C we get different kinds of problems [try to solve −1=(√x)]

$$\mathrm{talking}\:\mathrm{of}\:``\mathrm{definition}''\:\mathrm{and}\:``\mathrm{range}''\:\mathrm{makes} \\ $$$$\mathrm{no}\:\mathrm{sense}\:\mathrm{for}\:{x}\notin\mathbb{R}\:\mathrm{usually}. \\ $$$${y}=\sqrt{{x}}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:{x}\geqslant\mathrm{0}\:\mathrm{and}\:\mathrm{its}\:\mathrm{range}\:\mathrm{is}\:\left[\mathrm{0};\:+\infty\right) \\ $$$$\mathrm{for}\:{x}\in\mathbb{C}\:\mathrm{we}\:\mathrm{get}\:\mathrm{different}\:\mathrm{kinds}\:\mathrm{of}\:\mathrm{problems} \\ $$$$\left[\mathrm{try}\:\mathrm{to}\:\mathrm{solve}\:−\mathrm{1}=\sqrt{{x}}\right] \\ $$

Commented by M±th+et£s last updated on 24/Apr/20

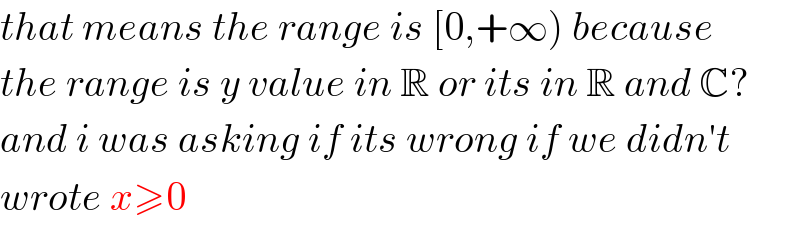
that means the range is [0,+∞) because the range is y value in R or its in R and C? and i was asking if its wrong if we didn′t wrote x≥0

$${that}\:{means}\:{the}\:{range}\:{is}\:\left[\mathrm{0},+\infty\right)\:{because} \\ $$$${the}\:{range}\:{is}\:{y}\:{value}\:{in}\:\mathbb{R}\:{or}\:{its}\:{in}\:\mathbb{R}\:{and}\:\mathbb{C}? \\ $$$${and}\:{i}\:{was}\:{asking}\:{if}\:{its}\:{wrong}\:{if}\:{we}\:{didn}'{t} \\ $$$${wrote}\:{x}\geqslant\mathrm{0}\: \\ $$

Commented by MJS last updated on 24/Apr/20

first you must specify the underlying set for x and for y i.e. f={(x, y)∣x∈N∧y∈N∧y=(√x)} or f={(x, y)∣x∈R∧y∈Z∧y=(√x)} or whatever is required usually, after having learned the rules for N, Z, Q and R you learn about functions with R→R or (x, y)∈R×R (=R^2 ) (x, y)∈C^2 is the last step so I guess we′re in R^2 in this case y=(√x) is not defined for x<0 and the range is [0; +∞) or simply y≥0. if only the range is asked for, y≥0 is enough

$$\mathrm{first}\:\mathrm{you}\:\mathrm{must}\:\mathrm{specify}\:\mathrm{the}\:\mathrm{underlying}\:\mathrm{set} \\ $$$$\mathrm{for}\:{x}\:\mathrm{and}\:\mathrm{for}\:{y} \\ $$$$\mathrm{i}.\mathrm{e}.\:{f}=\left\{\left({x},\:{y}\right)\mid{x}\in\mathbb{N}\wedge{y}\in\mathbb{N}\wedge{y}=\sqrt{{x}}\right\} \\ $$$$\mathrm{or}\:\:\:{f}=\left\{\left({x},\:{y}\right)\mid{x}\in\mathbb{R}\wedge{y}\in\mathbb{Z}\wedge{y}=\sqrt{{x}}\right\} \\ $$$$\mathrm{or}\:\mathrm{whatever}\:\mathrm{is}\:\mathrm{required} \\ $$$$\mathrm{usually},\:\mathrm{after}\:\mathrm{having}\:\mathrm{learned}\:\mathrm{the}\:\mathrm{rules}\:\mathrm{for} \\ $$$$\mathbb{N},\:\mathbb{Z},\:\mathbb{Q}\:\mathrm{and}\:\mathbb{R}\:\mathrm{you}\:\mathrm{learn}\:\mathrm{about}\:\mathrm{functions} \\ $$$$\mathrm{with}\:\mathbb{R}\rightarrow\mathbb{R}\:\mathrm{or}\:\left({x},\:{y}\right)\in\mathbb{R}×\mathbb{R}\:\left(=\mathbb{R}^{\mathrm{2}} \right) \\ $$$$\left({x},\:{y}\right)\in\mathbb{C}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{last}\:\mathrm{step} \\ $$$$\mathrm{so}\:\mathrm{I}\:\mathrm{guess}\:\mathrm{we}'\mathrm{re}\:\mathrm{in}\:\mathbb{R}^{\mathrm{2}} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:{y}=\sqrt{{x}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:{x}<\mathrm{0}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{range}\:\mathrm{is}\:\left[\mathrm{0};\:+\infty\right)\:\mathrm{or}\:\mathrm{simply}\:{y}\geqslant\mathrm{0}.\:\mathrm{if}\:\mathrm{only} \\ $$$$\mathrm{the}\:\mathrm{range}\:\mathrm{is}\:\mathrm{asked}\:\mathrm{for},\:{y}\geqslant\mathrm{0}\:\mathrm{is}\:\mathrm{enough} \\ $$

Commented by MJS last updated on 24/Apr/20

if we′re in C^2 it′s getting more complicated x∈C ⇔ x=e^(iθ) r with r∈R^+ and −π≤θ<π (?) here the complications start. some use 0≤θ<2π. some say (√(e^(iθ) r)) is not unique because y^2 =x has 2 solutions... but (√4)≠−2 even though (−2)^2 =4. which definitions to use depends on which kind of solution you need. y=(√x)=(√(e^(iθ) r))=e^(i(θ/2)) (√r) is unique if we define r≥0∧−π≤θ<π then y=(√x) is defined for x∈C but you cannot get y∈R^− because −π≤θ<π ⇔ −(π/2)≤(θ/2)<(π/2) ⇒ the range is y=e^(iφ) s; s∈R^+ ∧−(π/2)≤φ<(π/2) or y=a+bi; a∈R^+ ∧b∈R change the definitions above and you get different ranges

$$\mathrm{if}\:\mathrm{we}'\mathrm{re}\:\mathrm{in}\:\mathbb{C}^{\mathrm{2}} \:\mathrm{it}'\mathrm{s}\:\mathrm{getting}\:\mathrm{more}\:\mathrm{complicated} \\ $$$${x}\in\mathbb{C}\:\Leftrightarrow\:{x}=\mathrm{e}^{\mathrm{i}\theta} {r}\:\mathrm{with}\:{r}\in\mathbb{R}^{+} \:\mathrm{and}\:−\pi\leqslant\theta<\pi\:\left(?\right) \\ $$$$\mathrm{here}\:\mathrm{the}\:\mathrm{complications}\:\mathrm{start}.\:\mathrm{some}\:\mathrm{use} \\ $$$$\mathrm{0}\leqslant\theta<\mathrm{2}\pi.\:\mathrm{some}\:\mathrm{say}\:\sqrt{\mathrm{e}^{\mathrm{i}\theta} {r}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{unique}\:\mathrm{because} \\ $$$${y}^{\mathrm{2}} ={x}\:\mathrm{has}\:\mathrm{2}\:\mathrm{solutions}...\:\mathrm{but}\:\sqrt{\mathrm{4}}\neq−\mathrm{2}\:\mathrm{even}\:\mathrm{though} \\ $$$$\left(−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{4}.\:\mathrm{which}\:\mathrm{definitions}\:\mathrm{to}\:\mathrm{use}\:\mathrm{depends} \\ $$$$\mathrm{on}\:\mathrm{which}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{solution}\:\mathrm{you}\:\mathrm{need}. \\ $$$$ \\ $$$${y}=\sqrt{{x}}=\sqrt{\mathrm{e}^{\mathrm{i}\theta} {r}}=\mathrm{e}^{\mathrm{i}\frac{\theta}{\mathrm{2}}} \sqrt{{r}}\:\mathrm{is}\:\mathrm{unique}\:\mathrm{if}\:\mathrm{we}\:\mathrm{define} \\ $$$${r}\geqslant\mathrm{0}\wedge−\pi\leqslant\theta<\pi \\ $$$$\mathrm{then}\:{y}=\sqrt{{x}}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{C} \\ $$$$\mathrm{but}\:\mathrm{you}\:\mathrm{cannot}\:\mathrm{get}\:{y}\in\mathbb{R}^{−} \:\mathrm{because} \\ $$$$−\pi\leqslant\theta<\pi\:\Leftrightarrow\:−\frac{\pi}{\mathrm{2}}\leqslant\frac{\theta}{\mathrm{2}}<\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{range}\:\mathrm{is}\:{y}=\mathrm{e}^{\mathrm{i}\phi} {s};\:{s}\in\mathbb{R}^{+} \wedge−\frac{\pi}{\mathrm{2}}\leqslant\phi<\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{or}\:{y}={a}+{b}\mathrm{i};\:{a}\in\mathbb{R}^{+} \wedge{b}\in\mathbb{R} \\ $$$$ \\ $$$$\mathrm{change}\:\mathrm{the}\:\mathrm{definitions}\:\mathrm{above}\:\mathrm{and}\:\mathrm{you}\:\mathrm{get} \\ $$$$\mathrm{different}\:\mathrm{ranges} \\ $$

Commented by M±th+et£s last updated on 24/Apr/20

thank you verry much sir

$${thank}\:{you}\:{verry}\:{much}\:{sir}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com