Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 90589 by M±th+et£s last updated on 24/Apr/20

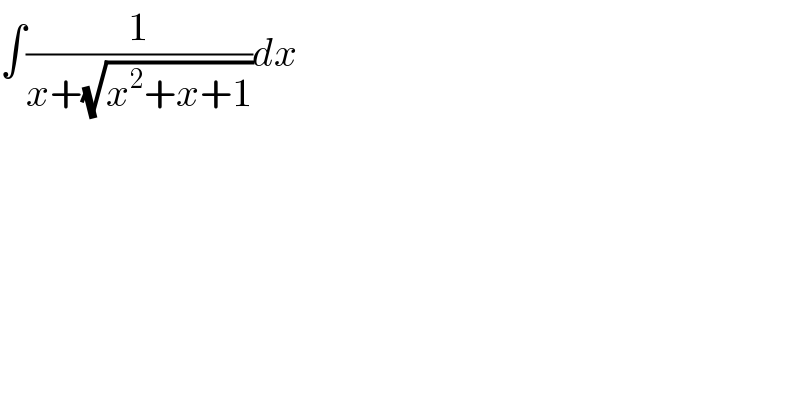
∫(1/(x+(√(x^2 +x+1))))dx

$$\int\frac{\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx} \\ $$

Commented by mathmax by abdo last updated on 24/Apr/20

I =∫ (dx/(x+(√(x^2 +x+1)))) =∫ (dx/(x+(√((x+(1/2))^2 +(3/4))))) changement x+(1/2)=((√3)/2)sh(t) ⇒ I =∫ (1/(((√3)/2)sh(t)−(1/2)+((√3)/2)ch(t)))×((√3)/2)ch(t)dt =(√3)∫ ((ch(t)dt)/((√3)sh(t)−1+(√3)ch(t))) =(√3)∫ (((e^t +e^(−t) )/2)/((√3)((e^t −e^(−t) )/2)−1+(√3)((e^t +e^(−t) )/2)))dt =(√3)∫ ((e^t +e^(−t) )/((√3)(e^t −e^(−t) )+(√3)(e^t +e^(−t) )−2))dt =_(e^t =u) (√3)∫ ((u+u^(−1) )/((√3)(u−u^(−1) )+(√3)(u+u^(−1) )−2)) (du/u) =(√3)∫ ((u^2 +1)/((√3)(u^3 −u)+(√3)(u^3 +u)−2u^2 ))du =(√3)∫ ((u^2 +1)/(2(√3)u^3 −2u^2 )) du =((√3)/2) ∫ ((u^2 +1)/(u^2 ((√3)u−1)))du let decompose F(u) =((u^2 +1)/(u^2 ((√3)u −1))) ⇒F(u) =(a/u) +(b/u^2 ) +(c/((√3)u−1)) b =−1 and c =4 ⇒F(u) =(a/u)−(1/u^2 ) +(4/((√3)u−1)) lim_(u→+∞) uF(u) =(1/(√3)) =a+(4/(√3)) ⇒a =(3/(√3))=(√3) ⇒ F(u) =((√3)/u) −(1/u^2 ) +(4/((√3)u −1)) ⇒ ∫ F(u)du =(√3)ln∣u∣+(1/u) +(4/(√3))ln∣(√3)u−1∣ +C =(√3)ln∣e^t ∣ + e^(−t) +(4/(√3))ln∣(√3)e^t −1∣ +C t =argsh(((2x+1)/(√3)))=ln(((2x+1)/(√3)) +(√(1+(((2x+1)/(√3)))^2 ))) ⇒ ∫F(u)du =(√3)(((2x+1)/(√3))+(√(1+(((2x+1)/(√3)))^2 )))+(1/(((2x+1)/(√3))+(√(1+(((2x+1)/(√3)))^2 )))) +(4/(√3))ln∣(√3)(((2x+1)/(√3)) +(√(1+(((2x+1)/(√3)))^2 )))−1∣ +C I =((√3)/2)∫ F(u)du

$${I}\:=\int\:\:\frac{{dx}}{{x}+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}\:=\int\:\:\frac{{dx}}{{x}+\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}} \\ $$$${changement}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\:\Rightarrow \\ $$$${I}\:=\int\:\:\:\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right)}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right){dt} \\ $$$$=\sqrt{\mathrm{3}}\int\:\:\:\frac{{ch}\left({t}\right){dt}}{\sqrt{\mathrm{3}}{sh}\left({t}\right)−\mathrm{1}+\sqrt{\mathrm{3}}{ch}\left({t}\right)}\:=\sqrt{\mathrm{3}}\int\:\:\frac{\frac{{e}^{{t}} +{e}^{−{t}} }{\mathrm{2}}}{\sqrt{\mathrm{3}}\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}−\mathrm{1}+\sqrt{\mathrm{3}}\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}}{dt} \\ $$$$=\sqrt{\mathrm{3}}\int\:\:\:\frac{{e}^{{t}} \:+{e}^{−{t}} }{\sqrt{\mathrm{3}}\left({e}^{{t}} −{e}^{−{t}} \right)+\sqrt{\mathrm{3}}\left({e}^{{t}} +{e}^{−{t}} \right)−\mathrm{2}}{dt} \\ $$$$=_{{e}^{{t}} ={u}} \:\:\sqrt{\mathrm{3}}\int\:\:\frac{{u}+{u}^{−\mathrm{1}} }{\sqrt{\mathrm{3}}\left({u}−{u}^{−\mathrm{1}} \right)+\sqrt{\mathrm{3}}\left({u}+{u}^{−\mathrm{1}} \right)−\mathrm{2}}\:\frac{{du}}{{u}} \\ $$$$=\sqrt{\mathrm{3}}\int\:\:\frac{{u}^{\mathrm{2}} +\mathrm{1}}{\sqrt{\mathrm{3}}\left({u}^{\mathrm{3}} −{u}\right)+\sqrt{\mathrm{3}}\left({u}^{\mathrm{3}} +{u}\right)−\mathrm{2}{u}^{\mathrm{2}} }{du} \\ $$$$=\sqrt{\mathrm{3}}\int\:\:\frac{{u}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}{u}^{\mathrm{3}} −\mathrm{2}{u}^{\mathrm{2}} }\:{du}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\int\:\:\frac{{u}^{\mathrm{2}} \:+\mathrm{1}}{{u}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{u}−\mathrm{1}\right)}{du}\:{let}\:{decompose} \\ $$$${F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} \:+\mathrm{1}}{{u}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{u}\:−\mathrm{1}\right)}\:\Rightarrow{F}\left({u}\right)\:=\frac{{a}}{{u}}\:+\frac{{b}}{{u}^{\mathrm{2}} }\:+\frac{{c}}{\sqrt{\mathrm{3}}{u}−\mathrm{1}}\: \\ $$$${b}\:=−\mathrm{1}\:{and}\:{c}\:=\mathrm{4}\:\Rightarrow{F}\left({u}\right)\:=\frac{{a}}{{u}}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\:+\frac{\mathrm{4}}{\sqrt{\mathrm{3}}{u}−\mathrm{1}} \\ $$$${lim}_{{u}\rightarrow+\infty} {uF}\left({u}\right)\:=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:={a}+\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}\:\Rightarrow{a}\:=\frac{\mathrm{3}}{\sqrt{\mathrm{3}}}=\sqrt{\mathrm{3}}\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\frac{\sqrt{\mathrm{3}}}{{u}}\:−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\:+\frac{\mathrm{4}}{\sqrt{\mathrm{3}}{u}\:−\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({u}\right){du}\:=\sqrt{\mathrm{3}}{ln}\mid{u}\mid+\frac{\mathrm{1}}{{u}}\:+\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}{ln}\mid\sqrt{\mathrm{3}}{u}−\mathrm{1}\mid\:+{C} \\ $$$$=\sqrt{\mathrm{3}}{ln}\mid{e}^{{t}} \mid\:+\:{e}^{−{t}} \:+\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}{ln}\mid\sqrt{\mathrm{3}}{e}^{{t}} −\mathrm{1}\mid\:+{C} \\ $$$${t}\:={argsh}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right)={ln}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$$\int{F}\left({u}\right){du}\:=\sqrt{\mathrm{3}}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right)+\frac{\mathrm{1}}{\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }} \\ $$$$+\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}{ln}\mid\sqrt{\mathrm{3}}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right)−\mathrm{1}\mid\:+{C} \\ $$$${I}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int\:{F}\left({u}\right){du} \\ $$$$ \\ $$

Commented by M±th+et£s last updated on 25/Apr/20

god bless you

$${god}\:{bless}\:{you} \\ $$

Commented by turbo msup by abdo last updated on 25/Apr/20

you are welcome sir.

$${you}\:{are}\:{welcome}\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com