find nature of the serie Σ (−1)^n U_n with U_(n+1) =(e^(−U_n ) /(n+1)) (U


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 90743 by abdomathmax last updated on 25/Apr/20

$f i n d n a t u r e o f t h e s e r i e Σ {(- 1)}^{n} U_{n}$ $w i t h U_{n + 1} = \frac{e^{- U_{n}}}{n + 1} (U_{0} = 1)$
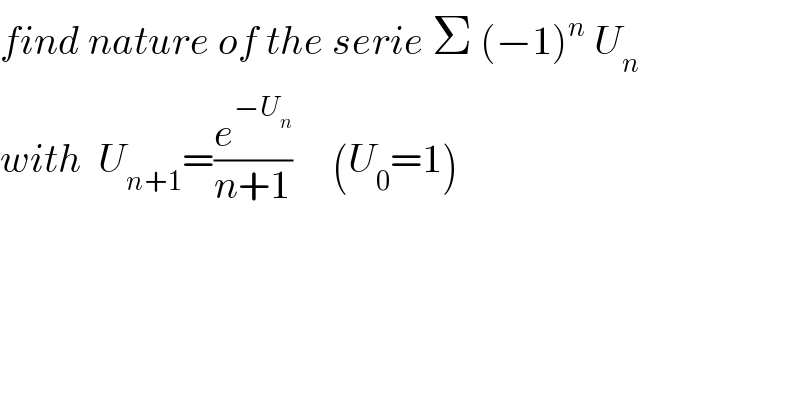
	Answered by ~blr237~ last updated on 25/Apr/20

	$w e c a n s h o w b y i n d u c t i o n t h a t U_{n} \in] 0, 1]$ $s o Σ {(- 1)}^{n} U_{n} i s a n a l t e r n a t e d s e r i e t h e n i t c o n v e r g e s$ $i f (U_{n}) d e c r e a s e a n d c o n v e r g e s t o z e r o .$ $w e h a v e e^{- u_{n}} < u_{n}; \frac{1}{n + 1} ⩽ 1 t h e n u_{n + 1} < u_{n}$ $∣ u_{n} ∣⩽ \frac{1}{n} c a u s e e^{- u_{n}} < 1 . s o \lim_{n \to \infty} u_{n} = 0$
	Commented by mathmax by abdo last updated on 25/Apr/20

	$t h a n k x s i r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum