
Question and Answers Forum
Question Number 90759 by M±th+et+s last updated on 25/Apr/20
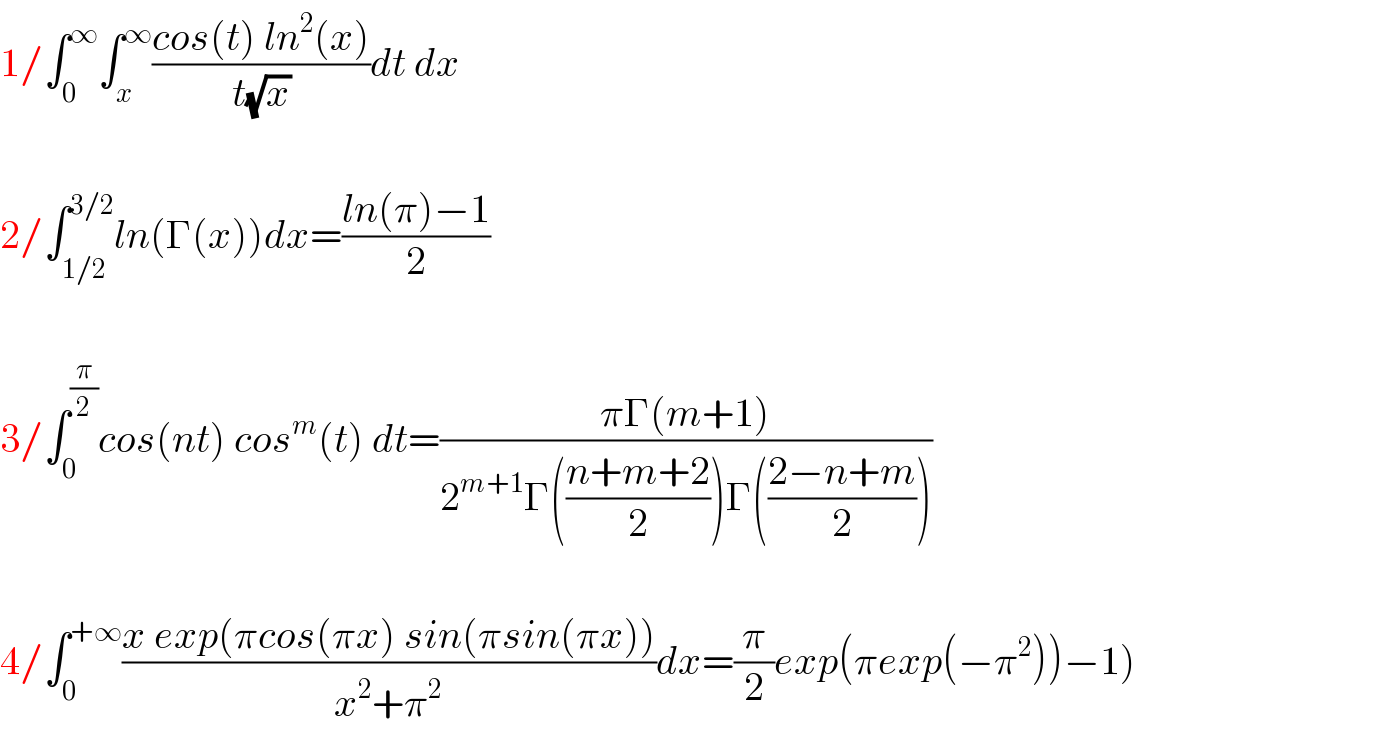
Commented by abdomathmax last updated on 26/Apr/20
![1) let take a try I=∫_0 ^∞ ∫_x ^∞ ((cost ln^2 x)/(t(√x)))dt dx by inversion we get I =∫_0 ^∞ (∫_0 ^t ((ln^2 x)/(√x)))((cost)/t)dt but ∫_0 ^t ((ln^2 x)/(√x))dx =_((√x)=u) ∫_0 ^(√t) ((ln^2 (u^2 ))/u)(2u)du =8 ∫_0 ^(√t) ln^2 u du and by psrts ∫_0 ^(√t) ln^2 u du =[u ln^2 u]_0 ^(√t) −∫_0 ^(√t) u ×((2lnu)/u) du =(√t)ln^2 ((√t))−2 ∫_0 ^(√t) lnu du =(1/4)(√t)ln^2 (t)−2[ulnu−u]_0 ^(√t) =(1/4)(√t)ln^2 (t)−2((√t)ln((√t))−(√t)) =(1/4)(√t)ln^2 (t)−(√t)ln(t)+2(√t) =(1/4)(√t)ln^2 (t)−(√t)ln(t)+2(√t) ⇒ ∫_0 ^t ((ln^2 x)/(√x))dx =2(√t)ln^2 (t)−8(√t)ln(t)+16(√t) ⇒ I =∫_0 ^∞ (2(√t)ln^2 (t)−8(√t)ln(t)+16(√t))((cost)/t)dt =_((√t)=z) ∫_0 ^∞ (2zln^2 (z^2 )−8zln(z^2 )+16z)((cos(z^2 ))/z^2 )(2z)dz =∫_0 ^∞ (4ln^2 (z^2 )−16ln(z^2 )+32)cos(z^2 )dz =8∫_0 ^∞ ln^2 (z)cos(z^2 )dz−32 ∫_0 ^∞ ln(z)cos(z^2 )dz +32 ∫_0 ^∞ cos(z^2 )dz ∫_0 ^∞ cos(z^2 )dz =Re(∫_0 ^∞ e^(−iz^2 ) dz) ∫_0 ^∞ e^(−iz^2 ) dz =∫_0 ^∞ e^(−((√i)z)^2 ) dz =_((√i)z =u) ∫_0 ^∞ e^(−u^2 ) (du/(√i)) =(1/e^((iπ)/4) ) ×((√π)/2) =((√π)/2)((1/(√2))−(i/(√2))) ⇒∫_0 ^∞ cos(z^2 )dz =((√π)/(2(√2))) ...be continuesd...](Q90782.png)
| ||
Question and Answers Forum | ||
Question Number 90759 by M±th+et+s last updated on 25/Apr/20 | ||
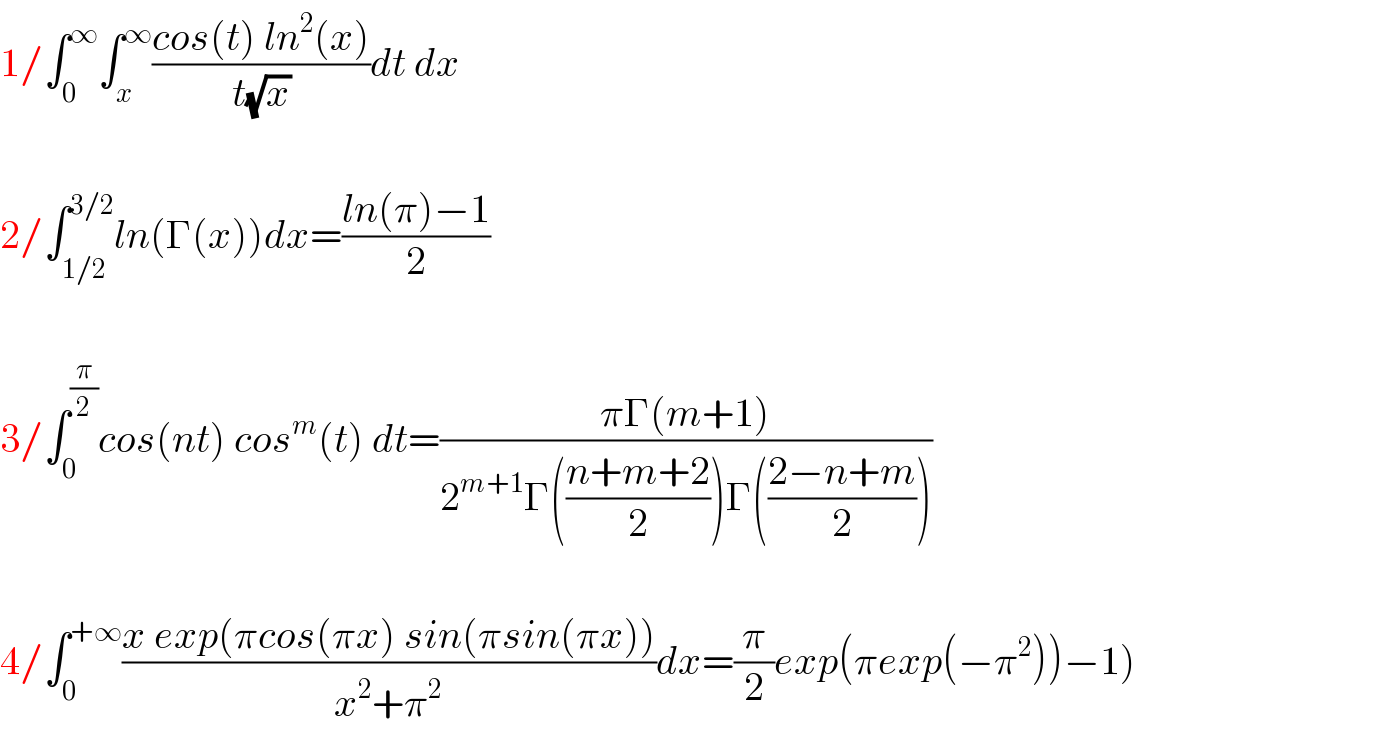 | ||
Commented by abdomathmax last updated on 26/Apr/20 | ||
![1) let take a try I=∫_0 ^∞ ∫_x ^∞ ((cost ln^2 x)/(t(√x)))dt dx by inversion we get I =∫_0 ^∞ (∫_0 ^t ((ln^2 x)/(√x)))((cost)/t)dt but ∫_0 ^t ((ln^2 x)/(√x))dx =_((√x)=u) ∫_0 ^(√t) ((ln^2 (u^2 ))/u)(2u)du =8 ∫_0 ^(√t) ln^2 u du and by psrts ∫_0 ^(√t) ln^2 u du =[u ln^2 u]_0 ^(√t) −∫_0 ^(√t) u ×((2lnu)/u) du =(√t)ln^2 ((√t))−2 ∫_0 ^(√t) lnu du =(1/4)(√t)ln^2 (t)−2[ulnu−u]_0 ^(√t) =(1/4)(√t)ln^2 (t)−2((√t)ln((√t))−(√t)) =(1/4)(√t)ln^2 (t)−(√t)ln(t)+2(√t) =(1/4)(√t)ln^2 (t)−(√t)ln(t)+2(√t) ⇒ ∫_0 ^t ((ln^2 x)/(√x))dx =2(√t)ln^2 (t)−8(√t)ln(t)+16(√t) ⇒ I =∫_0 ^∞ (2(√t)ln^2 (t)−8(√t)ln(t)+16(√t))((cost)/t)dt =_((√t)=z) ∫_0 ^∞ (2zln^2 (z^2 )−8zln(z^2 )+16z)((cos(z^2 ))/z^2 )(2z)dz =∫_0 ^∞ (4ln^2 (z^2 )−16ln(z^2 )+32)cos(z^2 )dz =8∫_0 ^∞ ln^2 (z)cos(z^2 )dz−32 ∫_0 ^∞ ln(z)cos(z^2 )dz +32 ∫_0 ^∞ cos(z^2 )dz ∫_0 ^∞ cos(z^2 )dz =Re(∫_0 ^∞ e^(−iz^2 ) dz) ∫_0 ^∞ e^(−iz^2 ) dz =∫_0 ^∞ e^(−((√i)z)^2 ) dz =_((√i)z =u) ∫_0 ^∞ e^(−u^2 ) (du/(√i)) =(1/e^((iπ)/4) ) ×((√π)/2) =((√π)/2)((1/(√2))−(i/(√2))) ⇒∫_0 ^∞ cos(z^2 )dz =((√π)/(2(√2))) ...be continuesd...](Q90782.png) | ||