
Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 90770 by ajfour last updated on 26/Apr/20
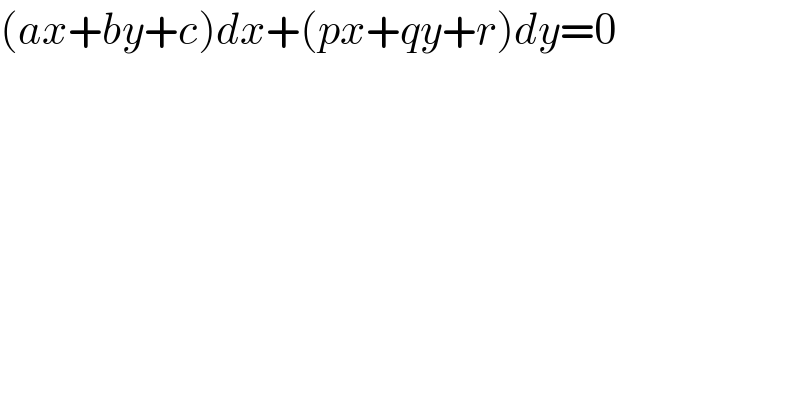
Answered by mr W last updated on 26/Apr/20
![(dy/dx)=−((ax+by+c)/(px+qy+r)) let x=u+u_0 , y=v+v_0 ax+by+c=a(u+u_0 )+b(v+v_0 )+c=au+bv+au_0 +bv_0 +c px+qy+r=p(u+u_0 )+q(v+v_0 )+r=pu+qv+pu_0 +qv_0 +r set au_0 +bv_0 +c=0 set pu_0 +qv_0 +r=0 ⇒u_0 =((−cq+rb)/(aq−bp)) ⇒v_0 =((−cp+ra)/(aq−bp)) (dy/dx)=(dv/du)=((au+bv)/(pu+qv)) let v=ut (dv/du)=t+u(dt/du) t+u(dt/du)=((a+bt)/(p+qt)) u(dt/du)=((a+bt)/(p+qt))−t=−((qt^2 +(p−b)t−a)/(qt+p)) ((qt+p)/(qt^2 +(p−b)t−a))dt=−(du/u) ∫((t+(p/q))/(t^2 +((p/q)−(b/q))t−(a/q)))dt=−∫(du/u) ∫((t+C)/(t^2 +At+B))dt=−∫(du/u) (1/2)ln (t^2 +At+B)+(C−(A/2))∫(dt/(t^2 +At+B))=−∫(du/u) (1/2)ln (t^2 +At+B)+((2C−A)/(√(4B−A^2 ))) tan^(−1) ((2t+A)/(√(4B−A^2 )))=−ln u+K (here only case 4B−A^2 >0, for cases 4B−A^2 ≤0 similarly) ⇒(1/2)ln [(((y−v_0 )/(x−u_0 )))^2 +A(((y−v_0 )/(x−u_0 )))+B]+((2C−A)/(√(4B−A^2 ))) tan^(−1) ((2(((y−v_0 )/(x−u_0 )))+A)/(√(4B−A^2 )))+ln (x−u_0 )=K](Q90776.png)
Commented by ajfour last updated on 26/Apr/20

| ||
Question and Answers Forum | ||
Previous in Differential Equation Next in Differential Equation | ||
Question Number 90770 by ajfour last updated on 26/Apr/20 | ||
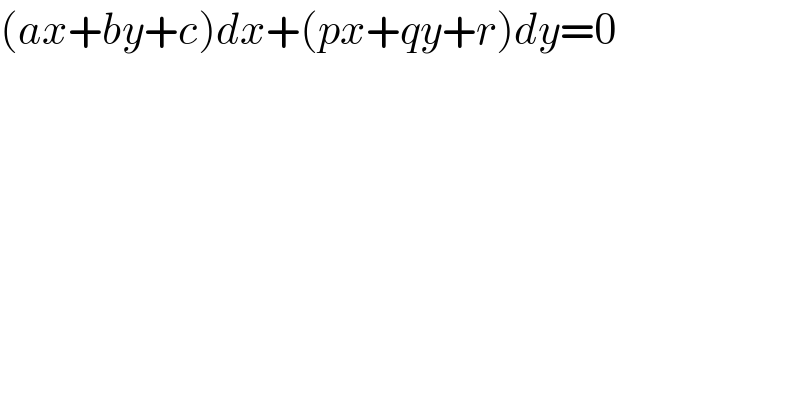 | ||
Answered by mr W last updated on 26/Apr/20 | ||
![(dy/dx)=−((ax+by+c)/(px+qy+r)) let x=u+u_0 , y=v+v_0 ax+by+c=a(u+u_0 )+b(v+v_0 )+c=au+bv+au_0 +bv_0 +c px+qy+r=p(u+u_0 )+q(v+v_0 )+r=pu+qv+pu_0 +qv_0 +r set au_0 +bv_0 +c=0 set pu_0 +qv_0 +r=0 ⇒u_0 =((−cq+rb)/(aq−bp)) ⇒v_0 =((−cp+ra)/(aq−bp)) (dy/dx)=(dv/du)=((au+bv)/(pu+qv)) let v=ut (dv/du)=t+u(dt/du) t+u(dt/du)=((a+bt)/(p+qt)) u(dt/du)=((a+bt)/(p+qt))−t=−((qt^2 +(p−b)t−a)/(qt+p)) ((qt+p)/(qt^2 +(p−b)t−a))dt=−(du/u) ∫((t+(p/q))/(t^2 +((p/q)−(b/q))t−(a/q)))dt=−∫(du/u) ∫((t+C)/(t^2 +At+B))dt=−∫(du/u) (1/2)ln (t^2 +At+B)+(C−(A/2))∫(dt/(t^2 +At+B))=−∫(du/u) (1/2)ln (t^2 +At+B)+((2C−A)/(√(4B−A^2 ))) tan^(−1) ((2t+A)/(√(4B−A^2 )))=−ln u+K (here only case 4B−A^2 >0, for cases 4B−A^2 ≤0 similarly) ⇒(1/2)ln [(((y−v_0 )/(x−u_0 )))^2 +A(((y−v_0 )/(x−u_0 )))+B]+((2C−A)/(√(4B−A^2 ))) tan^(−1) ((2(((y−v_0 )/(x−u_0 )))+A)/(√(4B−A^2 )))+ln (x−u_0 )=K](Q90776.png) | ||
| ||
Commented by ajfour last updated on 26/Apr/20 | ||
 | ||