∫_0 ^(√3) (1/(1+x^2 ))sin^(−1) (((2x)/(1+x^2 )))dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 90796 by M±th+et+s last updated on 26/Apr/20

$\int_{0}^{\sqrt{3}} \frac{1}{1 + x^{2}} {s i n}^{- 1} (\frac{2 x}{1 + x^{2}}) d x$
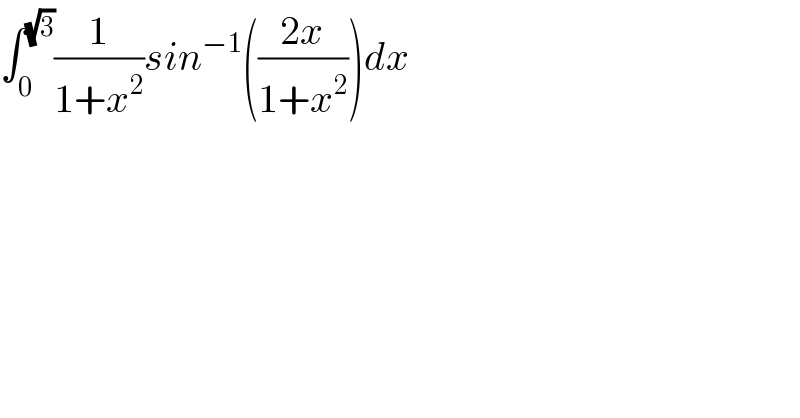
Commented by mathmax by abdo last updated on 26/Apr/20

$I = \int_{0}^{\sqrt{3}} \frac{1}{1 + x^{2}} a r c s i n (\frac{2 x}{1 + x^{2}}) d x c y a n g e m e n t x = t a n θ g i v e$ $I = \int_{0}^{\frac{π}{3}} \frac{1}{1 + {t a n}^{2} θ} a r c s i n (s i n (2 θ)) (1 + {t a n}^{2} θ) d θ$ $= \int_{0}^{\frac{π}{3}} 2 θ d θ = {[θ^{2}]}_{0}^{\frac{π}{3}} = \frac{π^{2}}{9}$
Commented by M±th+et+s last updated on 27/Apr/20

$t h a n x s i r b u t t h e l i m i t h a s t o b e d i v i d e f r o m$ $0 t o 1 t h e n 1 t o \sqrt{3}$
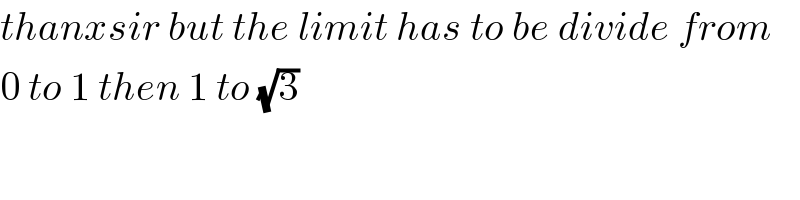
Commented by mathmax by abdo last updated on 28/Apr/20

$n o s i r t h e l i m i t s g o f r o m a r c t a n (0) = 0 t o a r c t a n (\sqrt{3}) = \frac{π}{3}$
	Answered by TANMAY PANACEA. last updated on 26/Apr/20

	$\int \frac{1}{1 + x^{2}} {s i n}^{- 1} (\frac{2 x}{1 + x^{2}}) d x$ $x = t a n a$ $\int \frac{1}{{s e c}^{2} a} \times {s i n}^{- 1} (s i n 2 a) {s e c}^{2} a d a$ $a^{2}$ $s o a n s w e r$ ${[∣ {t a n}^{- 1} x ∣_{0}^{\sqrt{3}}]}^{2} \to {(\frac{π}{3})}^{2} = \frac{π^{2}}{9}$
	Commented by M±th+et+s last updated on 26/Apr/20

	$i t h i n k i t s \frac{7 π^{2}}{72}$
	Answered by M±th+et+s last updated on 28/Apr/20

	$I = \int_{0}^{\frac{π}{3}} \frac{1}{1 + {t a n}^{2} θ} {s i n}^{- 1} (\frac{2 t a n θ}{1 + {t a n}^{2} (x)}) d (t a n θ)$ $= \int_{0}^{\frac{π}{3}} {c o s}^{2} (θ) {s i n}^{- 1} (s i n 2 θ) \frac{1}{{c o s}^{2} (θ)} d θ$ $\int_{0}^{\frac{π}{3}} {s i n}^{- 1} (2 θ) d θ$ $t h e l a s t t r i c k y!$ ${s i n}^{- 1} s i n θ \neq θ, θ > [\frac{π}{2}]! (1)$ $t h i s i s b e c a u s e {s i n}^{- 1} (θ) t o b e a f u n c t i o n$ $i t m u s t d e f i n e d a s a m a p p i n g o n l y$ $t o s u b - r e g i o n o f R .$ $s p e c i f i c a l l y :$ ${s i n}^{- 1} : [- 1, 1] \to [\frac{- π}{2}, \frac{π}{2}]$ $: x \to θ = {s i n}^{- 1} (x)$ $t h e r e f o r e . f o l l o w i n g g i v e s a o n e t o o n e$ $m a p p i n g :$ ${s i n}^{- 1} s i n : [\frac{- π}{2}, \frac{π}{2}] \to [\frac{- π}{2}, \frac{π}{2}]$ $i n o u r c a s e t h e a r g u m e n t i s 2 θ s o o u r$ $r a n g e g e t c o p a r e s s e d b y a f a c t o r o f t w o$ $s o w e g e t o l l o w i n g o n e t o m a n y m a p p i n g :$ ${s i n}^{- 1} s i n (2 \times_) : [\frac{- π}{4}, \frac{π}{4}] \to [\frac{- π}{2}, \frac{π}{2}]$ $w i t h a l i t t i l e t h o u g h t w e c a n e x t a n d$ $p a s t \frac{π}{4} t o \frac{π}{2} a n d o b t a i n f o l l o w i n g p l o t$ $o f {s i n}^{- 1} s i n 2 θ w i t h θ \in [0, \frac{π}{2}] w h i c h$ $i s a o n e t o m a n y m a p p i n g :$ $s o t h e i n t e g r a l i s j u s t t h e a r e a u n d e r$ $t h e c u r v e f r o m 0 t o π / 3 b r e a k i n g t h i s$ $u p :$ $\Rightarrow f o r θ \in [0, \frac{π}{4}], t h e a r e a o f t h e t r i a n g l e$ $i s \frac{π^{2}}{16} .$ $\Rightarrow f o r θ \in [\frac{π}{4}, \frac{π}{3}], t h e a r e a t r a p e z i o d$ $i s 5 π^{2} / 144$ $s u m m i n g t h e s e t w o, g i v e s$ $\frac{7 π^{2}}{72} (2)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum