
Question and Answers Forum
Question Number 90802 by john santu last updated on 26/Apr/20
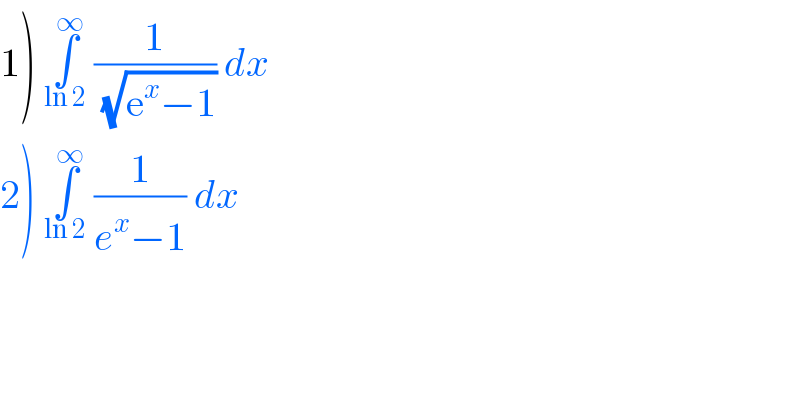
Commented by john santu last updated on 26/Apr/20
![1) u = (√(e^x −1)) ⇒ dx = ((2u du)/e^x ) ∫ _1 ^∞ ((2u)/u) (1/e^x ) du = ∫_1 ^∞ 2 (du/(u^2 +1)) = tan^(−1) (u) ]_1 ^∞ = 2((π/2)−(π/4)) = (π/2) 2)∫_(ln 2) ^∞ (e^(−x) /((e^x −1)e^(−x) )) dx = ∫_(ln 2) ^∞ (e^(−x) /(1−e^(−x) )) dx = ln (1−e^(−x) )]_(ln 2 ) ^∞ = 0 − ln ((1/2)) = ln 2](Q90805.png)
Commented by mathmax by abdo last updated on 26/Apr/20
![2) ∫_(ln2) ^∞ (dx/(e^x −1)) =_(e^x =t) ∫_2 ^∞ (dt/(t(t−1))) =∫_2 ^∞ ((1/(t−1))−(1/t))dt =[ln∣((t−1)/t)∣]_2 ^(+∞) =−ln((1/2))=ln(2)](Q90888.png)
| ||
Question and Answers Forum | ||
Question Number 90802 by john santu last updated on 26/Apr/20 | ||
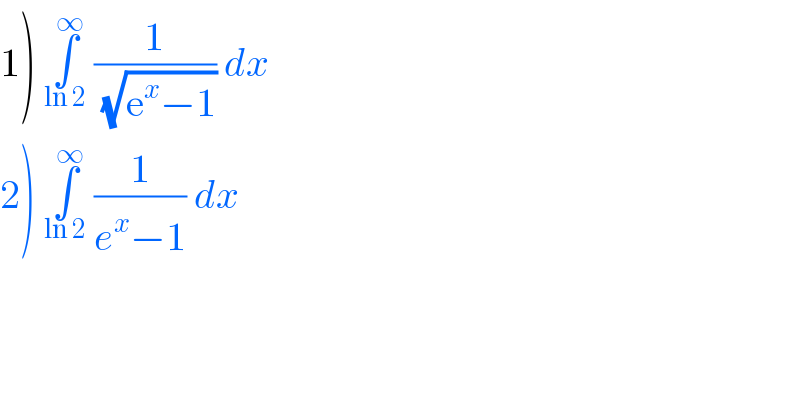 | ||
Commented by john santu last updated on 26/Apr/20 | ||
![1) u = (√(e^x −1)) ⇒ dx = ((2u du)/e^x ) ∫ _1 ^∞ ((2u)/u) (1/e^x ) du = ∫_1 ^∞ 2 (du/(u^2 +1)) = tan^(−1) (u) ]_1 ^∞ = 2((π/2)−(π/4)) = (π/2) 2)∫_(ln 2) ^∞ (e^(−x) /((e^x −1)e^(−x) )) dx = ∫_(ln 2) ^∞ (e^(−x) /(1−e^(−x) )) dx = ln (1−e^(−x) )]_(ln 2 ) ^∞ = 0 − ln ((1/2)) = ln 2](Q90805.png) | ||
Commented by mathmax by abdo last updated on 26/Apr/20 | ||
![2) ∫_(ln2) ^∞ (dx/(e^x −1)) =_(e^x =t) ∫_2 ^∞ (dt/(t(t−1))) =∫_2 ^∞ ((1/(t−1))−(1/t))dt =[ln∣((t−1)/t)∣]_2 ^(+∞) =−ln((1/2))=ln(2)](Q90888.png) | ||