Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 90842 by jagoll last updated on 26/Apr/20

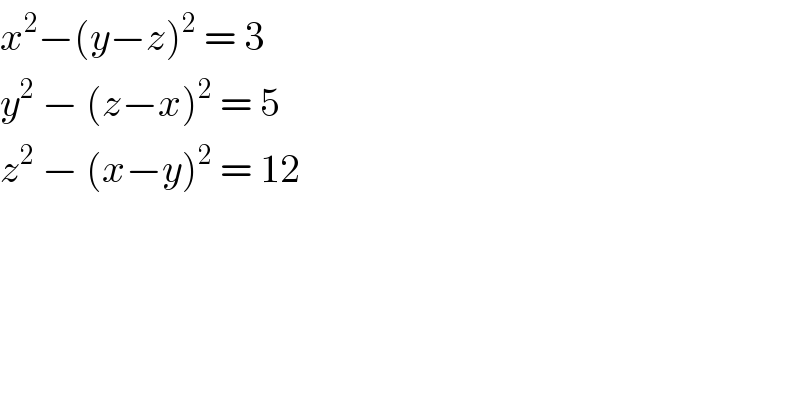
x^2 −(y−z)^2 = 3 y^2 − (z−x)^2 = 5 z^2 − (x−y)^2 = 12

$${x}^{\mathrm{2}} −\left({y}−{z}\right)^{\mathrm{2}} \:=\:\mathrm{3} \\ $$$${y}^{\mathrm{2}} \:−\:\left({z}−{x}\right)^{\mathrm{2}} \:=\:\mathrm{5} \\ $$$${z}^{\mathrm{2}} \:−\:\left({x}−{y}\right)^{\mathrm{2}} \:=\:\mathrm{12} \\ $$

Commented by john santu last updated on 26/Apr/20

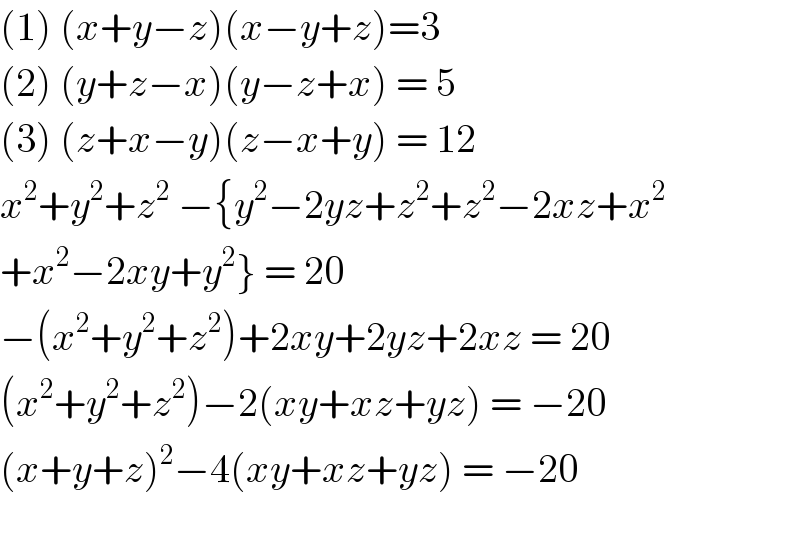
(1) (x+y−z)(x−y+z)=3 (2) (y+z−x)(y−z+x) = 5 (3) (z+x−y)(z−x+y) = 12 x^2 +y^2 +z^2 −{y^2 −2yz+z^2 +z^2 −2xz+x^2 +x^2 −2xy+y^2 } = 20 −(x^2 +y^2 +z^2 )+2xy+2yz+2xz = 20 (x^2 +y^2 +z^2 )−2(xy+xz+yz) = −20 (x+y+z)^2 −4(xy+xz+yz) = −20

$$\left(\mathrm{1}\right)\:\left({x}+{y}−{z}\right)\left({x}−{y}+{z}\right)=\mathrm{3} \\ $$$$\left(\mathrm{2}\right)\:\left({y}+{z}−{x}\right)\left({y}−{z}+{x}\right)\:=\:\mathrm{5} \\ $$$$\left(\mathrm{3}\right)\:\left({z}+{x}−{y}\right)\left({z}−{x}+{y}\right)\:=\:\mathrm{12} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:−\left\{{y}^{\mathrm{2}} −\mathrm{2}{yz}+{z}^{\mathrm{2}} +{z}^{\mathrm{2}} −\mathrm{2}{xz}+{x}^{\mathrm{2}} \right. \\ $$$$\left.+{x}^{\mathrm{2}} −\mathrm{2}{xy}+{y}^{\mathrm{2}} \right\}\:=\:\mathrm{20} \\ $$$$−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)+\mathrm{2}{xy}+\mathrm{2}{yz}+\mathrm{2}{xz}\:=\:\mathrm{20} \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)−\mathrm{2}\left({xy}+{xz}+{yz}\right)\:=\:−\mathrm{20} \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{2}} −\mathrm{4}\left({xy}+{xz}+{yz}\right)\:=\:−\mathrm{20} \\ $$$$ \\ $$

Commented by jagoll last updated on 26/Apr/20

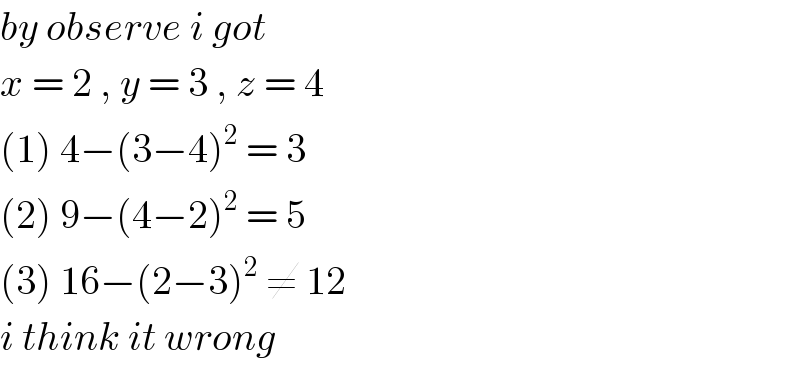
by observe i got x = 2 , y = 3 , z = 4 (1) 4−(3−4)^2 = 3 (2) 9−(4−2)^2 = 5 (3) 16−(2−3)^2 ≠ 12 i think it wrong

$${by}\:{observe}\:{i}\:{got}\: \\ $$$${x}\:=\:\mathrm{2}\:,\:{y}\:=\:\mathrm{3}\:,\:{z}\:=\:\mathrm{4}\: \\ $$$$\left(\mathrm{1}\right)\:\mathrm{4}−\left(\mathrm{3}−\mathrm{4}\right)^{\mathrm{2}} \:=\:\mathrm{3}\: \\ $$$$\left(\mathrm{2}\right)\:\mathrm{9}−\left(\mathrm{4}−\mathrm{2}\right)^{\mathrm{2}} \:=\:\mathrm{5}\: \\ $$$$\left(\mathrm{3}\right)\:\mathrm{16}−\left(\mathrm{2}−\mathrm{3}\right)^{\mathrm{2}} \:\neq\:\mathrm{12} \\ $$$${i}\:{think}\:{it}\:{wrong}\: \\ $$

Commented by Prithwish Sen 1 last updated on 26/Apr/20

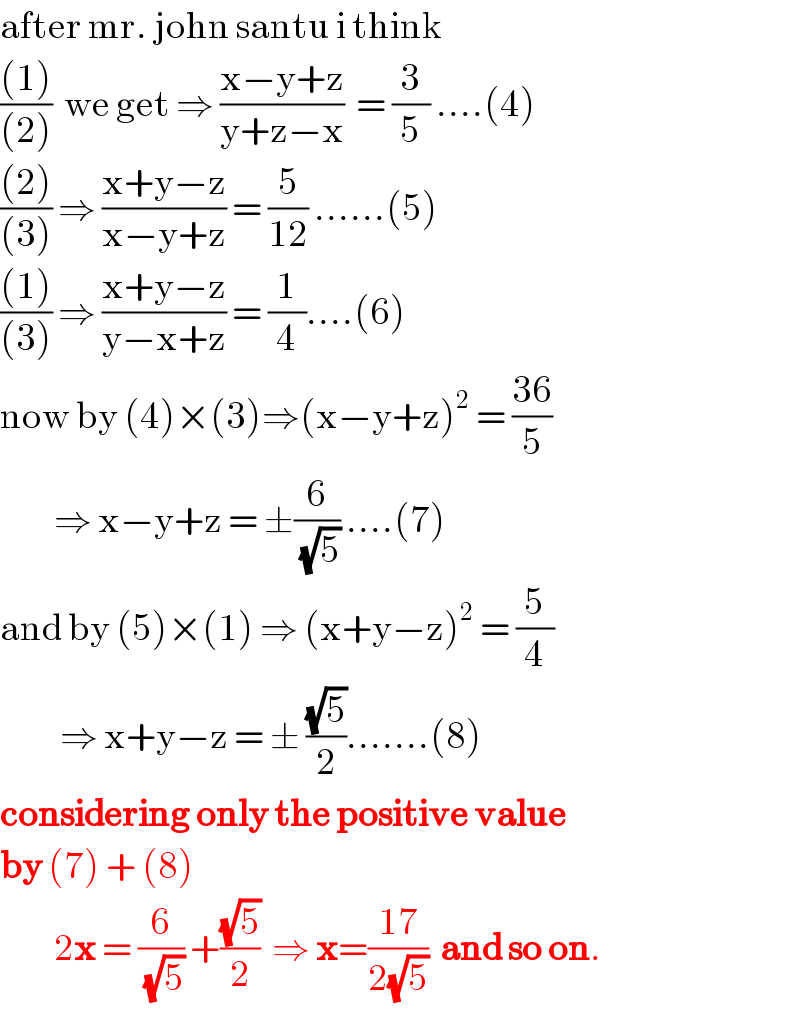
after mr. john santu i think (((1))/((2))) we get ⇒ ((x−y+z)/(y+z−x)) = (3/5) ....(4) (((2))/((3))) ⇒ ((x+y−z)/(x−y+z)) = (5/(12)) ......(5) (((1))/((3))) ⇒ ((x+y−z)/(y−x+z)) = (1/4)....(6) now by (4)×(3)⇒(x−y+z)^2 = ((36)/5) ⇒ x−y+z = ±(6/(√5)) ....(7) and by (5)×(1) ⇒ (x+y−z)^2 = (5/4) ⇒ x+y−z = ± ((√5)/2).......(8) considering only the positive value by (7) + (8) 2x = (6/(√5)) +((√5)/2) ⇒ x=((17)/(2(√5))) and so on.

$$\mathrm{after}\:\mathrm{mr}.\:\mathrm{john}\:\mathrm{santu}\:\mathrm{i}\:\mathrm{think} \\ $$$$\frac{\left(\mathrm{1}\right)}{\left(\mathrm{2}\right)}\:\:\mathrm{we}\:\mathrm{get}\:\Rightarrow\:\frac{\mathrm{x}−\mathrm{y}+\mathrm{z}}{\mathrm{y}+\mathrm{z}−\mathrm{x}}\:\:=\:\frac{\mathrm{3}}{\mathrm{5}}\:....\left(\mathrm{4}\right) \\ $$$$\frac{\left(\mathrm{2}\right)}{\left(\mathrm{3}\right)}\:\Rightarrow\:\frac{\mathrm{x}+\mathrm{y}−\mathrm{z}}{\mathrm{x}−\mathrm{y}+\mathrm{z}}\:=\:\frac{\mathrm{5}}{\mathrm{12}}\:......\left(\mathrm{5}\right) \\ $$$$\frac{\left(\mathrm{1}\right)}{\left(\mathrm{3}\right)}\:\Rightarrow\:\frac{\mathrm{x}+\mathrm{y}−\mathrm{z}}{\mathrm{y}−\mathrm{x}+\mathrm{z}}\:=\:\frac{\mathrm{1}}{\mathrm{4}}....\left(\mathrm{6}\right) \\ $$$$\mathrm{now}\:\mathrm{by}\:\left(\mathrm{4}\right)×\left(\mathrm{3}\right)\Rightarrow\left(\mathrm{x}−\mathrm{y}+\mathrm{z}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{36}}{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{x}−\mathrm{y}+\mathrm{z}\:=\:\pm\frac{\mathrm{6}}{\sqrt{\mathrm{5}}}\:....\left(\mathrm{7}\right) \\ $$$$\mathrm{and}\:\mathrm{by}\:\left(\mathrm{5}\right)×\left(\mathrm{1}\right)\:\Rightarrow\:\left(\mathrm{x}+\mathrm{y}−\mathrm{z}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{x}+\mathrm{y}−\mathrm{z}\:=\:\pm\:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}.......\left(\mathrm{8}\right) \\ $$$$\boldsymbol{\mathrm{considering}}\:\boldsymbol{\mathrm{only}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{positive}}\:\boldsymbol{\mathrm{value}} \\ $$$$\boldsymbol{\mathrm{by}}\:\left(\mathrm{7}\right)\:+\:\left(\mathrm{8}\right)\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2}\boldsymbol{\mathrm{x}}\:=\:\frac{\mathrm{6}}{\sqrt{\mathrm{5}}}\:+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:\Rightarrow\:\boldsymbol{\mathrm{x}}=\frac{\mathrm{17}}{\mathrm{2}\sqrt{\mathrm{5}}}\:\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{on}}. \\ $$

Commented by jagoll last updated on 28/Apr/20

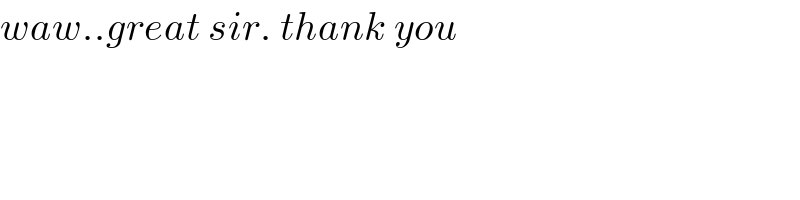
waw..great sir. thank you

$${waw}..{great}\:{sir}.\:{thank}\:{you} \\ $$

Answered by ajfour last updated on 26/Apr/20

x^2 −y^2 −z^2 =3−2yz ..(i) y^2 −z^2 −x^2 =5−2xz ...(ii) z^2 −x^2 −y^2 =12−2xy ....(iii) Adding all (x^2 +y^2 +z^2 )−2(xy+yz+zx)=−20 ⇒ (x+y)^2 −2z(x+y)−4xy+z^2 =−20 .....(I) (i)+(ii) 2z(x+y)−2z^2 =8 ⇒ x+y=z+(4/z) from (III) ⇒ (x−y)^2 =z^2 −12 (i)−(ii) (x^2 −y^2 )−z(x−y)=−1 ⇒ (x−y)(x+y−z)=−1 (x−y)^2 {(x+y)^2 +z^2 −2z(x+y)}=1 (z^2 −12){(z+(4/z))^2 +z^2 −2z(z+(4/z))}=1 (z^2 −12)(((16)/z^2 ))=1 16z^2 −192=z^2 ⇒ z^2 =((192)/(15))=((64)/5) (x+y)^2 =((64)/5)+((16×5)/(64))+8 = ((64)/5)+(5/4)+8 = ((441)/(20)) (x−y)^2 =z^2 −12 =((64)/5)−12=(4/5) let x>y ⇒ x−y=(4/(√(20))) , x+y=((21)/(√(20))) ⇒x=((25)/(4(√5))) , y=((17)/(4(√5))) , z=((32)/(4(√5))) . these dont fit very well, so let x<y ⇒ y−x=(4/(√(20))) ⇒ x=((17)/(4(√5))) , y=((25)/(4(√5))) , z=((32)/(4(√5)))

$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} −{z}^{\mathrm{2}} =\mathrm{3}−\mathrm{2}{yz}\:\:\:..\left({i}\right) \\ $$$${y}^{\mathrm{2}} −{z}^{\mathrm{2}} −{x}^{\mathrm{2}} =\mathrm{5}−\mathrm{2}{xz}\:\:\:\:\:...\left({ii}\right) \\ $$$${z}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{12}−\mathrm{2}{xy}\:\:\:\:\:....\left({iii}\right) \\ $$$${Adding}\:\:{all} \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)−\mathrm{2}\left({xy}+{yz}+{zx}\right)=−\mathrm{20} \\ $$$$\Rightarrow\:\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{z}\left({x}+{y}\right)−\mathrm{4}{xy}+{z}^{\mathrm{2}} =−\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....\left({I}\right) \\ $$$$\left({i}\right)+\left({ii}\right) \\ $$$$\mathrm{2}{z}\left({x}+{y}\right)−\mathrm{2}{z}^{\mathrm{2}} =\mathrm{8}\:\:\: \\ $$$$\Rightarrow\:\:{x}+{y}={z}+\frac{\mathrm{4}}{{z}} \\ $$$${from}\:\left({III}\right)\: \\ $$$$\Rightarrow\:\:\left({x}−{y}\right)^{\mathrm{2}} ={z}^{\mathrm{2}} −\mathrm{12} \\ $$$$\left({i}\right)−\left({ii}\right) \\ $$$$\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)−{z}\left({x}−{y}\right)=−\mathrm{1} \\ $$$$\Rightarrow\:\left({x}−{y}\right)\left({x}+{y}−{z}\right)=−\mathrm{1} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} \left\{\left({x}+{y}\right)^{\mathrm{2}} +{z}^{\mathrm{2}} −\mathrm{2}{z}\left({x}+{y}\right)\right\}=\mathrm{1} \\ $$$$\left({z}^{\mathrm{2}} −\mathrm{12}\right)\left\{\left({z}+\frac{\mathrm{4}}{{z}}\right)^{\mathrm{2}} +{z}^{\mathrm{2}} −\mathrm{2}{z}\left({z}+\frac{\mathrm{4}}{{z}}\right)\right\}=\mathrm{1} \\ $$$$\left({z}^{\mathrm{2}} −\mathrm{12}\right)\left(\frac{\mathrm{16}}{{z}^{\mathrm{2}} }\right)=\mathrm{1} \\ $$$$\mathrm{16}{z}^{\mathrm{2}} −\mathrm{192}={z}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{z}^{\mathrm{2}} =\frac{\mathrm{192}}{\mathrm{15}}=\frac{\mathrm{64}}{\mathrm{5}} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} =\frac{\mathrm{64}}{\mathrm{5}}+\frac{\mathrm{16}×\mathrm{5}}{\mathrm{64}}+\mathrm{8}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{64}}{\mathrm{5}}+\frac{\mathrm{5}}{\mathrm{4}}+\mathrm{8}\:=\:\frac{\mathrm{441}}{\mathrm{20}} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} ={z}^{\mathrm{2}} −\mathrm{12}\:=\frac{\mathrm{64}}{\mathrm{5}}−\mathrm{12}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${let}\:{x}>{y} \\ $$$$\Rightarrow\:\:\:{x}−{y}=\frac{\mathrm{4}}{\sqrt{\mathrm{20}}}\:\:,\:\:{x}+{y}=\frac{\mathrm{21}}{\sqrt{\mathrm{20}}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{25}}{\mathrm{4}\sqrt{\mathrm{5}}}\:,\:\:{y}=\frac{\mathrm{17}}{\mathrm{4}\sqrt{\mathrm{5}}}\:,\:\:{z}=\frac{\mathrm{32}}{\mathrm{4}\sqrt{\mathrm{5}}}\:. \\ $$$${these}\:{dont}\:{fit}\:{very}\:{well},\:{so}\:{let} \\ $$$$\:\:\:\:\:\:{x}<{y}\:\:\Rightarrow\:\:{y}−{x}=\frac{\mathrm{4}}{\sqrt{\mathrm{20}}} \\ $$$$\Rightarrow\:\:{x}=\frac{\mathrm{17}}{\mathrm{4}\sqrt{\mathrm{5}}}\:,\:\:{y}=\frac{\mathrm{25}}{\mathrm{4}\sqrt{\mathrm{5}}}\:,\:\:{z}=\frac{\mathrm{32}}{\mathrm{4}\sqrt{\mathrm{5}}} \\ $$

Commented by ajfour last updated on 26/Apr/20

i checked them even, hurray!

$${i}\:{checked}\:{them}\:{even},\:{hurray}! \\ $$

Commented by jagoll last updated on 26/Apr/20

hHaha hurray sir

$${hHaha}\:{hurray}\:{sir}\: \\ $$

Answered by mr W last updated on 26/Apr/20

(x+y−z)(x−y+z)=3 (x+y+z−2z)(x+y+z−2y)=3 ...(i) (y+z−x)(y−z+x)=5 (x+y+z−2x)(x+y+z−2z)=5 ...(ii) (z+x−y)(z−x+y)=12 (x+y+z−2y)(x+y+z−2x)=12 ...(iii) (i)×(ii)×(iii): (x+y+z−2x)^2 (x+y+z−2y)^2 (x+y+z−2z)^2 =3×5×12=180 (x+y+z−2x)(x+y+z−2y)(x+y+z−2z)=±6(√5) ...(iv) (iv)/(i) and similarly: x+y+z−2x=±((6(√5))/3) ... I x+y+z−2y=±((6(√5))/5) ...II x+y+z−2z=±((6(√5))/(12)) ...III I+II+III: x+y+z=±6(√5)((1/3)+(1/5)+(1/(12))) ...IV IV−I and similarly: 2x=±6(√5)((1/5)+(1/(12))) ⇒x=±((17(√5))/(20)) 2y=±6(√5)((1/3)+(1/(12))) ⇒y=±((5(√5))/4) 2z=±6(√5)((1/3)+(1/5)) ⇒z=±((8(√5))/5)

$$\left({x}+{y}−{z}\right)\left({x}−{y}+{z}\right)=\mathrm{3} \\ $$$$\left({x}+{y}+{z}−\mathrm{2}{z}\right)\left({x}+{y}+{z}−\mathrm{2}{y}\right)=\mathrm{3}\:\:\:...\left({i}\right) \\ $$$$\left({y}+{z}−{x}\right)\left({y}−{z}+{x}\right)=\mathrm{5} \\ $$$$\left({x}+{y}+{z}−\mathrm{2}{x}\right)\left({x}+{y}+{z}−\mathrm{2}{z}\right)=\mathrm{5}\:\:\:...\left({ii}\right) \\ $$$$\left({z}+{x}−{y}\right)\left({z}−{x}+{y}\right)=\mathrm{12} \\ $$$$\left({x}+{y}+{z}−\mathrm{2}{y}\right)\left({x}+{y}+{z}−\mathrm{2}{x}\right)=\mathrm{12}\:\:\:...\left({iii}\right) \\ $$$$ \\ $$$$\left({i}\right)×\left({ii}\right)×\left({iii}\right): \\ $$$$\left({x}+{y}+{z}−\mathrm{2}{x}\right)^{\mathrm{2}} \left({x}+{y}+{z}−\mathrm{2}{y}\right)^{\mathrm{2}} \left({x}+{y}+{z}−\mathrm{2}{z}\right)^{\mathrm{2}} =\mathrm{3}×\mathrm{5}×\mathrm{12}=\mathrm{180} \\ $$$$\left({x}+{y}+{z}−\mathrm{2}{x}\right)\left({x}+{y}+{z}−\mathrm{2}{y}\right)\left({x}+{y}+{z}−\mathrm{2}{z}\right)=\pm\mathrm{6}\sqrt{\mathrm{5}}\:\:\:...\left({iv}\right) \\ $$$$ \\ $$$$\left({iv}\right)/\left({i}\right)\:{and}\:{similarly}: \\ $$$${x}+{y}+{z}−\mathrm{2}{x}=\pm\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{3}}\:\:\:...\:{I} \\ $$$${x}+{y}+{z}−\mathrm{2}{y}=\pm\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{5}}\:\:\:...{II} \\ $$$${x}+{y}+{z}−\mathrm{2}{z}=\pm\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{12}}\:\:\:...{III} \\ $$$${I}+{II}+{III}: \\ $$$${x}+{y}+{z}=\pm\mathrm{6}\sqrt{\mathrm{5}}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{12}}\right)\:\:\:...{IV} \\ $$$$ \\ $$$${IV}−{I}\:{and}\:{similarly}: \\ $$$$\mathrm{2}{x}=\pm\mathrm{6}\sqrt{\mathrm{5}}\left(\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{12}}\right)\:\Rightarrow{x}=\pm\frac{\mathrm{17}\sqrt{\mathrm{5}}}{\mathrm{20}} \\ $$$$\mathrm{2}{y}=\pm\mathrm{6}\sqrt{\mathrm{5}}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{12}}\right)\:\Rightarrow{y}=\pm\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{2}{z}=\pm\mathrm{6}\sqrt{\mathrm{5}}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}\right)\:\Rightarrow{z}=\pm\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$

Commented by mr W last updated on 26/Apr/20

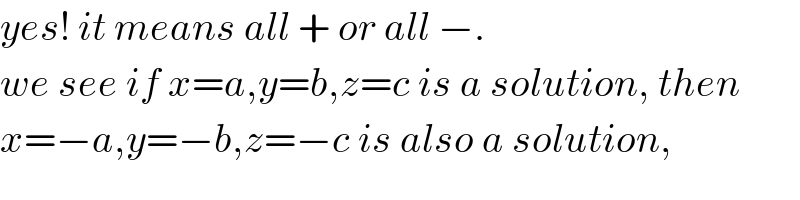
yes! it means all + or all −. we see if x=a,y=b,z=c is a solution, then x=−a,y=−b,z=−c is also a solution,

$${yes}!\:{it}\:{means}\:{all}\:+\:{or}\:{all}\:−. \\ $$$${we}\:{see}\:{if}\:{x}={a},{y}={b},{z}={c}\:{is}\:{a}\:{solution},\:{then} \\ $$$${x}=−{a},{y}=−{b},{z}=−{c}\:{is}\:{also}\:{a}\:{solution}, \\ $$

Commented by ajfour last updated on 26/Apr/20

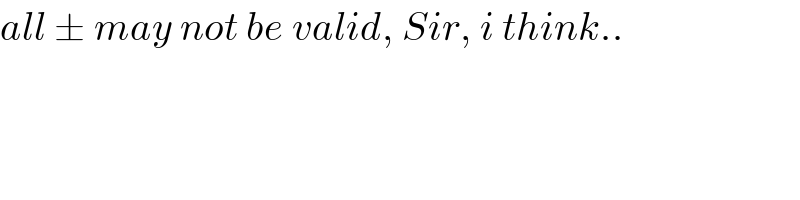
all ± may not be valid, Sir, i think..

$${all}\:\pm\:{may}\:{not}\:{be}\:{valid},\:{Sir},\:{i}\:{think}.. \\ $$

Commented by mr W last updated on 26/Apr/20

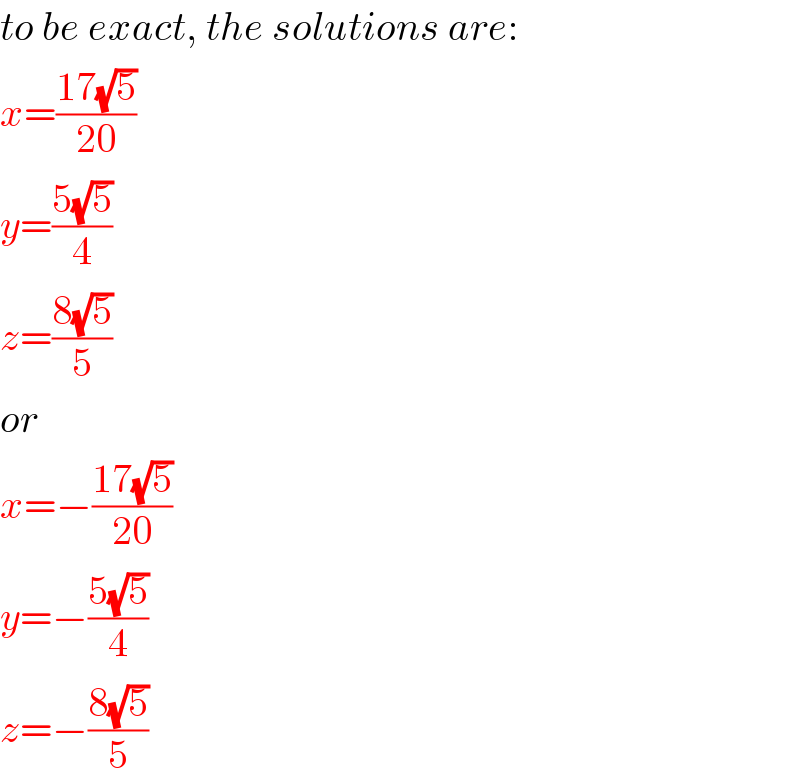
to be exact, the solutions are: x=((17(√5))/(20)) y=((5(√5))/4) z=((8(√5))/5) or x=−((17(√5))/(20)) y=−((5(√5))/4) z=−((8(√5))/5)

$${to}\:{be}\:{exact},\:{the}\:{solutions}\:{are}: \\ $$$${x}=\frac{\mathrm{17}\sqrt{\mathrm{5}}}{\mathrm{20}} \\ $$$${y}=\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$${z}=\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$$${or} \\ $$$${x}=−\frac{\mathrm{17}\sqrt{\mathrm{5}}}{\mathrm{20}} \\ $$$${y}=−\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$${z}=−\frac{\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$

Commented by ajfour last updated on 26/Apr/20

Thanks for clarifying Sir!

$${Thanks}\:{for}\:{clarifying}\:{Sir}! \\ $$

Commented by jagoll last updated on 26/Apr/20

great....

$${great}.... \\ $$

Commented by I want to learn more last updated on 27/Apr/20

Nice.

$$\mathrm{Nice}. \\ $$

Answered by MWSuSon last updated on 26/Apr/20

(x+y−z)(x−y+z)=3…(1) (y−z+x)(y+z−x)=5…(2) (z−x+y)(z+x−y)=12…(3) ((eqn(1))/(eqn(2))) (((x−y+z))/((y+z−x)))=(3/5)…(4) ((eqn(3))/(eqn(2))) (((z+x−y))/((y−z+x)))=((12)/5)…(5) ((eqn(1))/(eqn(3))) (((x+y−z))/((z−x+y)))=(3/(12))…(6) from eqn(4) 3y+3z−3x=5x−5y+5z 8y−2z−8x=0 [x−y=((−z)/4)] from eqn(5) 5z+5x−5y=12y−12z+12x 17z−7x−17y=0 [y−z=((−7x)/(17))] from eqn(6) 3z−3x+3y=12x+12y−12z [z−x=((9y)/(15))] input the value of (x−y) into eqn(3) input the value of (y−z) into eqn(1) input the value of (z−x) into eqn(2) and you′ll have the answer Mr W had.

$$\left({x}+{y}−{z}\right)\left({x}−{y}+{z}\right)=\mathrm{3}\ldots\left(\mathrm{1}\right) \\ $$$$\left({y}−{z}+{x}\right)\left({y}+{z}−{x}\right)=\mathrm{5}\ldots\left(\mathrm{2}\right) \\ $$$$\left({z}−{x}+{y}\right)\left({z}+{x}−{y}\right)=\mathrm{12}\ldots\left(\mathrm{3}\right) \\ $$$$\frac{{eqn}\left(\mathrm{1}\right)}{{eqn}\left(\mathrm{2}\right)}\:\:\:\frac{\left({x}−{y}+{z}\right)}{\left({y}+{z}−{x}\right)}=\frac{\mathrm{3}}{\mathrm{5}}\ldots\left(\mathrm{4}\right) \\ $$$$\frac{{eqn}\left(\mathrm{3}\right)}{{eqn}\left(\mathrm{2}\right)}\:\:\:\frac{\left({z}+{x}−{y}\right)}{\left({y}−{z}+{x}\right)}=\frac{\mathrm{12}}{\mathrm{5}}\ldots\left(\mathrm{5}\right) \\ $$$$\frac{{eqn}\left(\mathrm{1}\right)}{{eqn}\left(\mathrm{3}\right)}\:\:\:\frac{\left({x}+{y}−{z}\right)}{\left({z}−{x}+{y}\right)}=\frac{\mathrm{3}}{\mathrm{12}}\ldots\left(\mathrm{6}\right) \\ $$$${from}\:{eqn}\left(\mathrm{4}\right)\:\mathrm{3}{y}+\mathrm{3}{z}−\mathrm{3}{x}=\mathrm{5}{x}−\mathrm{5}{y}+\mathrm{5}{z} \\ $$$$\mathrm{8}{y}−\mathrm{2}{z}−\mathrm{8}{x}=\mathrm{0} \\ $$$$\left[{x}−{y}=\frac{−{z}}{\mathrm{4}}\right] \\ $$$${from}\:{eqn}\left(\mathrm{5}\right)\:\mathrm{5}{z}+\mathrm{5}{x}−\mathrm{5}{y}=\mathrm{12}{y}−\mathrm{12}{z}+\mathrm{12}{x} \\ $$$$\mathrm{17}{z}−\mathrm{7}{x}−\mathrm{17}{y}=\mathrm{0} \\ $$$$\left[{y}−{z}=\frac{−\mathrm{7}{x}}{\mathrm{17}}\right] \\ $$$${from}\:{eqn}\left(\mathrm{6}\right)\:\mathrm{3}{z}−\mathrm{3}{x}+\mathrm{3}{y}=\mathrm{12}{x}+\mathrm{12}{y}−\mathrm{12}{z} \\ $$$$\left[{z}−{x}=\frac{\mathrm{9}{y}}{\mathrm{15}}\right] \\ $$$${input}\:{the}\:{value}\:{of}\:\left({x}−{y}\right)\:{into}\:{eqn}\left(\mathrm{3}\right) \\ $$$${input}\:{the}\:{value}\:{of}\:\left({y}−{z}\right)\:{into}\:{eqn}\left(\mathrm{1}\right) \\ $$$${input}\:{the}\:{value}\:{of}\:\left({z}−{x}\right)\:{into}\:{eqn}\left(\mathrm{2}\right) \\ $$$${and}\:{you}'{ll}\:{have}\:{the}\:{answer}\:{Mr}\:{W}\:{had}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com