Previous in Differential Equation Next in Differential Equation
Question Number 90863 by ajfour last updated on 26/Apr/20
$$\frac{{dy}}{{dx}}−{a}\left(\frac{{y}}{{x}}\right)=\mathrm{1}+\frac{\mathrm{1}}{{x}} \\ $$
Answered by mr W last updated on 26/Apr/20
$${p}\left({x}\right)=−\frac{{a}}{{x}} \\ $$$$\int{p}\left({x}\right){dx}=−\int\frac{{a}}{{x}}{dx}=−{a}\mathrm{ln}\:{x}=\mathrm{ln}\:{x}^{−{a}} \\ $$$${u}\left({x}\right)={e}^{\int{p}\left({x}\right){dx}} ={x}^{−{a}} \\ $$$${q}\left({x}\right)=\mathrm{1}+\frac{\mathrm{1}}{{x}} \\ $$$$\int{u}\left({x}\right){q}\left({x}\right){dx}=\int{x}^{−{a}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right){dx}=−\frac{\mathrm{1}}{{a}−\mathrm{1}}{x}^{−{a}+\mathrm{1}} −\frac{\mathrm{1}}{{a}}{x}^{−{a}} \\ $$$${y}=\frac{\int{u}\left({x}\right){q}\left({x}\right){dx}+{C}}{{u}\left({x}\right)}=\frac{−\frac{\mathrm{1}}{{a}−\mathrm{1}}{x}^{−{a}+\mathrm{1}} −\frac{\mathrm{1}}{{a}}{x}^{−{a}} +{C}}{{x}^{−{a}} } \\ $$$$\Rightarrow{y}={Cx}^{{a}} −\frac{{x}}{{a}−\mathrm{1}}−\frac{\mathrm{1}}{{a}} \\ $$
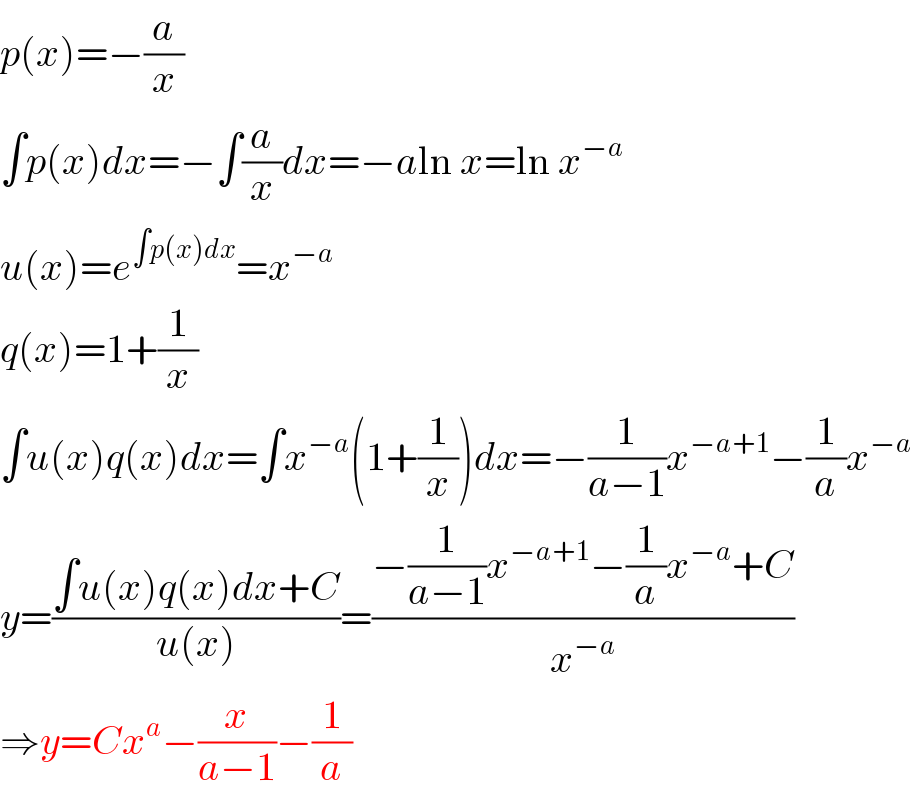
Commented by jagoll last updated on 26/Apr/20
$${exact}\:{diff}\:{eq}\:? \\ $$
Commented by mr W last updated on 26/Apr/20
Commented by jagoll last updated on 26/Apr/20
$${o}\:{yes}.\:{not}\:{exact}\: \\ $$
Commented by jagoll last updated on 26/Apr/20
Commented by ajfour last updated on 26/Apr/20
Absolutely perfect Sir!
Answered by mathmax by abdo last updated on 23/Jun/20
![y^′ −(a/x)y =((x+1)/x) ⇒xy^′ −ay =x+1 (e) (he)→xy^′ −ay =0 ⇒xy^′ =ay ⇒(y^′ /y) =(a/x) ⇒ln∣y∣ =aln∣x∣ +c ⇒ y =k ∣x∣^a solution on ]0,+∞[ ⇒y =k x^a mvc method →y^′ =k^′ x^a +ak x^(a−1) e⇒k^′ x^(a+1) +ak x^a −ka x^a =x+1 ⇒k^′ =((x+1)/x^(a+1) ) =(1/x^a ) +(1/x^(a+1) ) =x^(−a) +x^(−(a+1)) ⇒ k(x) =∫(x^(−a) +x^(−(a+1)) )dx =(1/(1−a))x^(1−a) −(1/a)x^(−a) +c ⇒ y(x) =((1/(1−a))x^(1−a) −(1/a)x^(−a) )x^a =(x/(1−a))−(1/a) with a≠1 and a≠0](Q99769.png)
$$\mathrm{y}^{'} −\frac{\mathrm{a}}{\mathrm{x}}\mathrm{y}\:=\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}\:\Rightarrow\mathrm{xy}^{'} −\mathrm{ay}\:=\mathrm{x}+\mathrm{1}\:\left(\mathrm{e}\right) \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{xy}^{'} −\mathrm{ay}\:=\mathrm{0}\:\Rightarrow\mathrm{xy}^{'} \:=\mathrm{ay}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=\frac{\mathrm{a}}{\mathrm{x}}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=\mathrm{aln}\mid\mathrm{x}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\left.\mathrm{y}\:=\mathrm{k}\:\mid\mathrm{x}\mid^{\mathrm{a}} \:\:\:\:\:\mathrm{solution}\:\mathrm{on}\:\right]\mathrm{0},+\infty\left[\:\:\Rightarrow\mathrm{y}\:=\mathrm{k}\:\mathrm{x}^{\mathrm{a}} \right. \\ $$$$\mathrm{mvc}\:\mathrm{method}\:\rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} \:\mathrm{x}^{\mathrm{a}} \:+\mathrm{ak}\:\mathrm{x}^{\mathrm{a}−\mathrm{1}} \\ $$$$\mathrm{e}\Rightarrow\mathrm{k}^{'} \:\mathrm{x}^{\mathrm{a}+\mathrm{1}} +\mathrm{ak}\:\mathrm{x}^{\mathrm{a}} −\mathrm{ka}\:\mathrm{x}^{\mathrm{a}} \:=\mathrm{x}+\mathrm{1}\:\Rightarrow\mathrm{k}^{'} \:=\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{a}+\mathrm{1}} }\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{a}} }\:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{a}+\mathrm{1}} }\:=\mathrm{x}^{−\mathrm{a}} \:+\mathrm{x}^{−\left(\mathrm{a}+\mathrm{1}\right)} \:\Rightarrow \\ $$$$\mathrm{k}\left(\mathrm{x}\right)\:=\int\left(\mathrm{x}^{−\mathrm{a}} +\mathrm{x}^{−\left(\mathrm{a}+\mathrm{1}\right)} \right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{a}}\mathrm{x}^{\mathrm{1}−\mathrm{a}} \:−\frac{\mathrm{1}}{\mathrm{a}}\mathrm{x}^{−\mathrm{a}} \:\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{a}}\mathrm{x}^{\mathrm{1}−\mathrm{a}} \:−\frac{\mathrm{1}}{\mathrm{a}}\mathrm{x}^{−\mathrm{a}} \right)\mathrm{x}^{\mathrm{a}} \:=\frac{\mathrm{x}}{\mathrm{1}−\mathrm{a}}−\frac{\mathrm{1}}{\mathrm{a}}\:\:\:\:\:\:\mathrm{with}\:\mathrm{a}\neq\mathrm{1}\:\mathrm{and}\:\mathrm{a}\neq\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 23/Jun/20
$$\mathrm{sorry}\:\mathrm{y}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{a}}\mathrm{x}^{\mathrm{1}−\mathrm{a}} −\frac{\mathrm{1}}{\mathrm{a}}\mathrm{x}^{−\mathrm{a}} \:+\mathrm{c}\right)\mathrm{x}^{\mathrm{a}} \:=\frac{\mathrm{x}}{\mathrm{1}−\mathrm{a}}−\frac{\mathrm{1}}{\mathrm{a}}\:+\mathrm{c}\:\mathrm{x}^{\mathrm{a}} \\ $$